Шпорки по Fиzиkе

Made by ПеJIbmеHb ©2008

Special thx to Юля & Ира

Сказать спасибо и пинать за ошибки можно в ICQ#477472

КВАНТОВАЯ ФИЗИКА

1. Что такое фотон?

Фотон - элементарная частица, масса покоя которой равна нулю, энергия , импульс .

— волновой вектор.

— циклическая частота.

— постоянная Планка.

2. Что такое фотоэффект?

Фотоэффект - вырывание электронов с поверхности вещества под действием света.

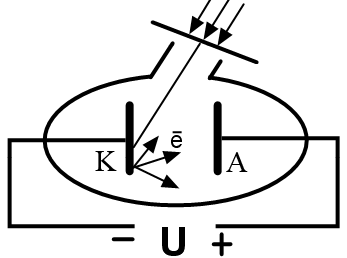
3. Уравнение Эйнштейна для фотоэффекта

При падении фотона на вещество происходит взаимодействие фотона с электроном вещества. Фотон поглощается, а его энергия передаётся электрону. Уравнение Эйнштейна:

— масса электрона.

— постоянная Планка.

— максимальная скорость вылетевших фотоэлектронов.

— работа выхода (работа, которую необходимо затратить, чтобы вытащить с поверхности вещества, сделать его свободным, не сообщая кин. энергии).

4. Что такое красная граница фотоэффекта?

Фотоэффект происходит, если частота света превышает некоторую критическую , которая называется красной границей фотоэффекта.

— не зависит от интенсивности, зависит от работы выхода.

— постоянная Планка.

— работа выхода фотокатода.

5. Что такое эффект Комптона?

Эффект Комптона - это изменение длины волны эл-маг. излучения из-за рассеяния его электронами. Эл-маг. излучение - это поток фотонов - частиц, с позиции корпускулярной теории, а рассеивание - столкновение фотона с вещества, при этом должен сохраняться закон сохранения энергии и импульса.

, при этом

— постоянная Планка.

— длинна волны рассеянного фотона.

— длинна волны фотона до рассеяния.

— угол рассеяния (угол между направлениями распр. фотона до и после рассеяния).

— постоянная Комптона (для ).

6. Что такое абсолютно чёрное тело?

Тело, которое полностью поглощает всё падающее на него излучение и ничего не отражает, называется абсолютно чёрным телом.

Пример модели чёрного тела - полость с небольшим отверстием и зачернёнными стенками. Свет, попадающий сквозь отверстие в полость, испытывает многократные отражения и сильно поглощается.

7. Излучающая способность чёрного тела (f и рисунок)

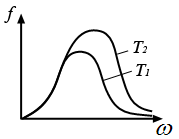
Формула Планка:

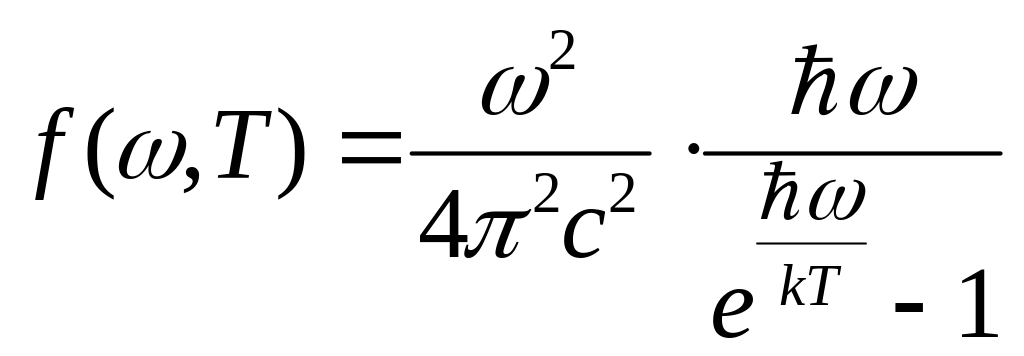
— температура чёрного тела.

— частота излучения.

— постоянная Планка.

— постоянная Больцмана.

— скорость света.

8. Физический смысл излучающей способности тела

Физический смысл излучающей способности - это энергия, излучившаяся с единицы поверхности нагретого тела в единичном интервале частот за единицу времени.

9. Закон Стефана - Больцмана

Общая энергия теплового излучения определяется законом Стефана - Больцмана:

— мощность на единицу площади излучающей поверхности.

— константа Стефана - Больцмана.

10. Модель атома Резерфорда. Недостатки модели

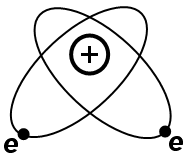
В центре — положительно заряженное ядро, в нёс собрана почти вся масса атома, . Вокруг ядра вращаются лёгкие отрицательно заряженные электроны, радиус электронной орбиты . Атом электрически нейтрален, заряд ядра по величине равен суммарному заряду электронов.

Недостаток модели — нестабильность такого атома. Ускоренно движущийся электрон излучал (терял) бы энергию и должен был бы упасть на ядро.

11. Постулаты Бора

1). Возможны лишь дискретные (стационарные) орбиты для электронов. Для этих орбит выполняется квантовое условие: , где , — постоянная Планка.

2). В стационарном состоянии электрон не излучает, излучение происходит при переходе между орбитами, выделяется (или поглощается) фотон с энергией (E - полная энергия).

12. В чём заключается гипотеза Де Бройля?

Де Бройль высказал гипотезу, что двойственная природа света (волна-частица) присуща и другим видам материи, а это означает, что то, что мы воспринимаем как частицы ( ), в некоторых ситуациях должно вести себя как волны.

Если частица имеет энергию и величину импульса , то ей соответствует волна Де Бройля.

Частота волны , длинна волны .

— постоянная Планка.

13. Приведите примеры корпускулярных явлений света, волновых явлений света и частиц

• Корпускулярные явления света:

фотоэффект, эффект Комптона, тепловое излучение, давление света.

• Волновые явления света:

интерференция, дифракция, поляризация.

• Волновые явления частиц:

дифракция электронов на кристалле, на фольге.

14. Временное уравнение Шредингера

— оператор Лапласа.

— мнимая единица.

— волновая функция.

— потенциальная энергия в точке и в момент времени.

— масса частицы.

— постоянная Планка.

15. Стационарное уравнение Шредингера

— оператор Лапласа.

— волновая функция.

— потенциальная энергия в точке.

— полная энергия частицы.

— масса частицы.

— постоянная Планка.

16. Физический смысл волновой функции

— вероятность нахождении частицы а элементе объёма .

Если частица находится в каком либо объёме , то на волновую функцию можно дополнительно наложить условие нормировки:

Смысл нормировки: вероятность нахождения частицы в объёме = 1.

Для нормированных волновых функций выполняется равенство:

17. Свойства волновой функции

1). Если — решение ур. Шредингера — тоже решение ( )

2). и — решение — решение (линейная комбинация)

3). Вероятностный смысл: однозначность, непрерывность, непрерывность I-ой производной, если не имеет бесконечного разрыва.

18. Соотношения неопределённостей Гейзенберга

Нельзя одновременно точно узнать координату и соответствующую проекцию импульса.

(в квантовой механике отсутствует понятие траектории частицы)

— постоянная Планка.

— неопределённость координаты x частицы.

— неопределённость проекции импульса частицы.

19. Что такое туннельный эффект? Явления, объясняемые туннельным эффектом

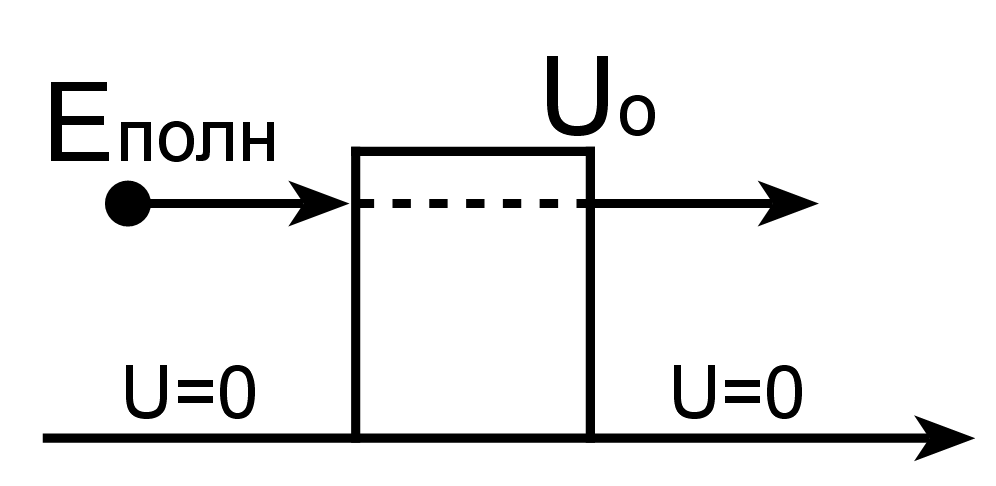
Туннельный эффект - преодоление частицей потенциального барьера в случае, когда её полная энергия меньше высоты барьера. Вероятность прохождения частицы через барьер тем больше, чем ниже и уже потенциальный барьер.

Явления, объясняемые туннельным эффектом:

• контактная разность потенциалов.

• холодная эмиссия электронов из катодов.

• многие явления в p-n переходах (полупроводники).

• -распад ядер.

20. Какие энергии может иметь частица в потенциальной яме?

Частица, находящаяся в потенциальной яме, может иметь только дискретные значения энергии, определяемые выражением:

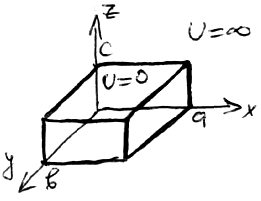
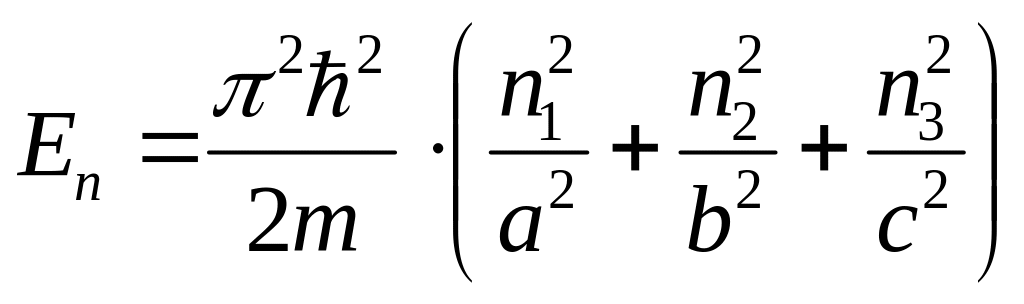, где = 1,2,3,...

— масса частицы.

— постоянная Планка.

— граница ящика.

21. Какие энергии может иметь гармонический осциллятор?

, где n = 0,1,2,...

— частота колебаний.

— постоянная Планка.

22. Какие энергии может иметь электрон в атоме водорода?

, где n = 1,2,3,...

— постоянная Ридберга.

23. Что такое вырождение по энергии в квантовой механике?

Явления, когда в разным квантовым состояниям (состояниям, описываемым разными квантовыми формулами) соответствует одна и та же энергия - называется вырождением по энергии. Это явление появляется всякий раз, когда появляется симметрия в потенциальной энергии.

24. Как построить квантовый оператор физической величины?

Каждой физической величине в квантовой механике сопоставляется оператор.

— квантовый оператор.

— собственное значение.

Координата:

Импульс:

Кин. энергия:

— градиент.

— оператор Лапласа.

25. Как вычислить среднее значение физической величины?

— градиент.

— волновая функция.

— мнимая единица.

— физическая величина.

— постоянная Планка.

26. Как вычислить возможные значения физической величины?

Возможные значения физической величины — это собственные значения соответствующего квантового оператора.

— возможные значения физ. величины.

— собственная функция данного дифференциального оператора.

27. Какие значения может иметь абсолютная величина момента импульса частицы?

, где l = 0,1,2,...

— постоянная Планка.

28. Какие значения может иметь величина проекции момента импульса частицы?

, где

— постоянная Планка.

— величина момента импульса.

— магнитное квантовое число.

29. Что такое спин?

Спин — собственный момент импульса элементарной частицы. Спин измеряется в единицах и равен , где — характерное для каждого сорта частиц целое (в т. ч. нулевое) или полу-целое положительное число — спиновое квантовое число.

• Целый спин — бозоны.

• Полу целый спин — фермионы.

СТАТИСТИЧЕСКАЯ ФИЗИКА

1. Определения идеального и неидеального газа

Газ является идеальным, если средняя потенциальная энергия взаимодействия между частицами много меньше, чем средняя кинетическая энергия частиц. В противном случае газ считается неидеальным.

— идеальный газ.

2. Определения классического и квантового газа

Газ считается классическим, если среднее расстояние между частицами газами много больше длинны волны Де-Бройля. В противном случае газ считается квантовым.

— классический газ.

— квантовый газ.

3. Перечислить основные микроскопические и макроскопические параметры газа

Микроскопические параметры — индивидуальные характеристики частиц:

— масса частицы,

— скорость частицы,

— кинетическая энергия частицы.

Макроскопические параметры — параметры газа как физического тела:

— давление,

— температура,

— концентрация молекул,

— объём.

4. Что такое равновесное состояние системы?

Если макроскопические параметры, описывающие изолированную систему, такие как: температура, давление, концентрация и др. не меняются во времени и одинаковы во всех частях системы, то говорят, что система находиться в равновесном состоянии.

5. Основное уравнение кинетической теории идеального газа

— давление.

— температура газа.

— масса молекулы газа.

— концентрация молекул газа.

— скорость теплового движения молекул.

— постоянная Больцмана.

6. Закон равнораспределения энергий молекул по степеням свободы

• На каждую степень свободы поступательного и вращательного движения молекулы приходиться средняя энергия .

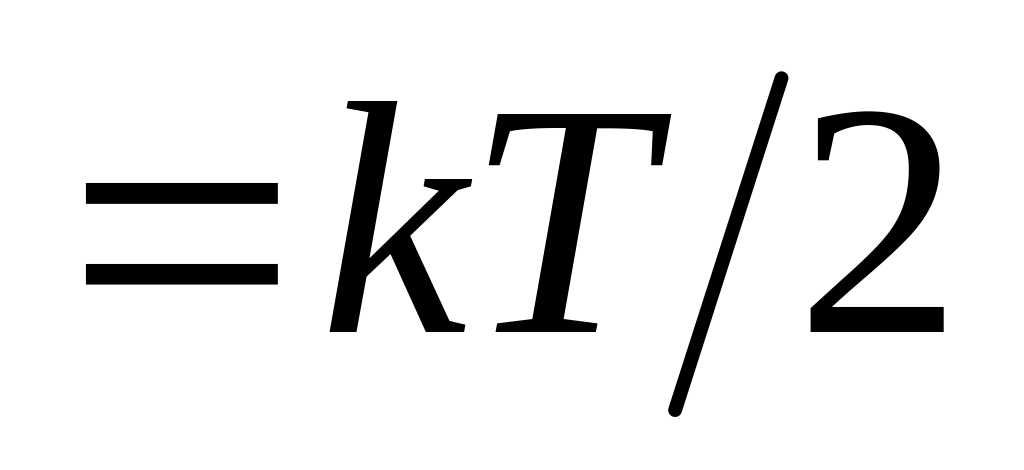• На каждую степень свободы колебательного движения приходиться средняя энергия (по 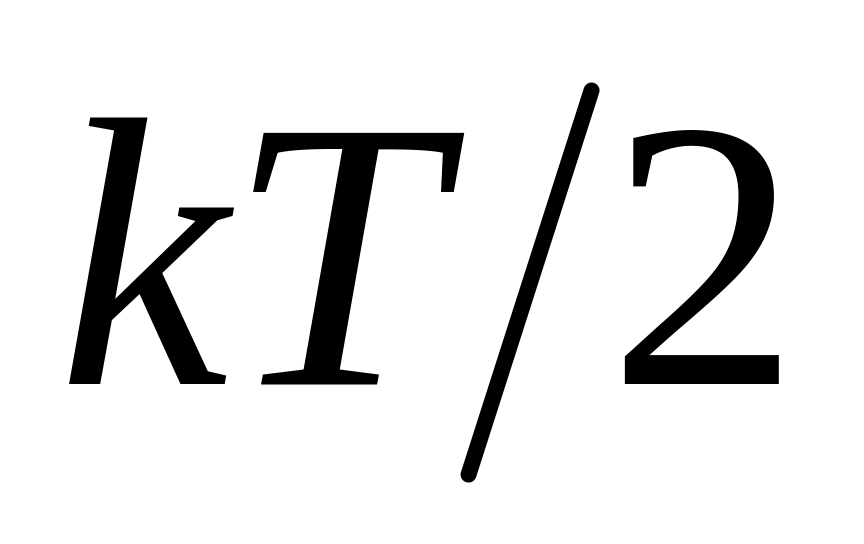на кинетическую и потенциальную энергию).

— температура газа.

— средняя энергия молекул газа.

— постоянная Больцмана.

7. Что такое степени свободы молекулы? Перечислить степени свободы молекул и

Степени свободы движения молекулы - это величины, с помощью которых можно однозначно задать положение молекул в пространстве.

(2 атома):

3 поступательных (ц.м.) + 2 вращательных + 1 колебательная

(3 атома):

3 поступательных (ц.м) + 3 вращательных + 2 колебательных

8. Что такое температура?

Температура является мерой внутренней энергии идеального газа в состоянии термодинамического равновесия.

— постоянная Больцмана.

— средняя кинетическая энергия молекул газа.

9. Сформулировать предположения из которых Максвелл получил свои распределения

а). В пространстве скоростей точки, соответствующие молекуле, будут расположены сферически симметрично (в силу равноправности направлений движения), т.е. плоскость этих точек в пространстве будет зависеть только от величины скорости.

б). Вероятность того, что молекула имеет какое-либо значение проекции скорости по одной оси не зависит от значений проекций скоростей по другим осям (проекции скоростей между собой не связаны).

10. Распределение Максвелла для проекции скорости молекул

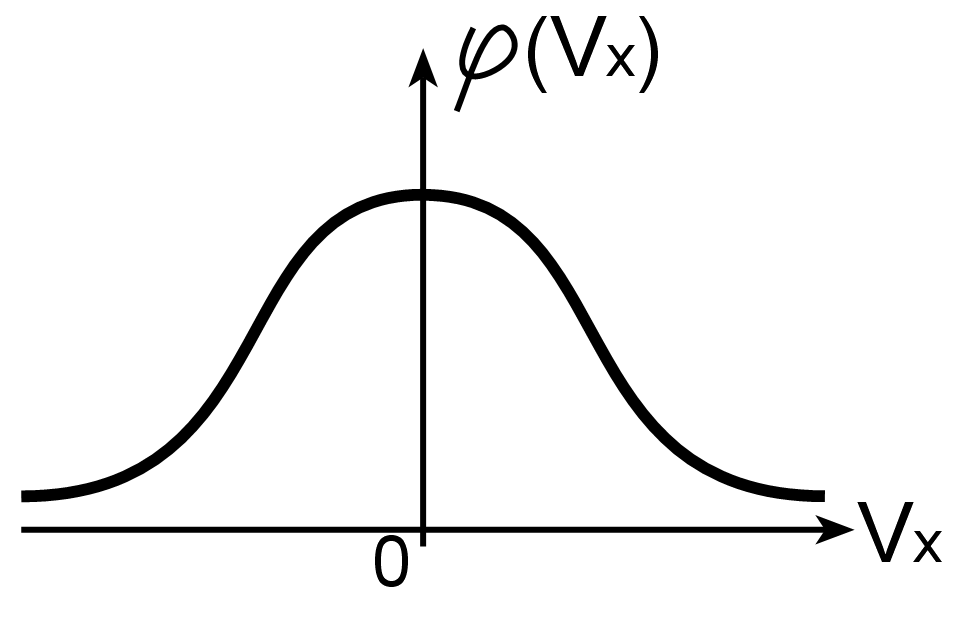
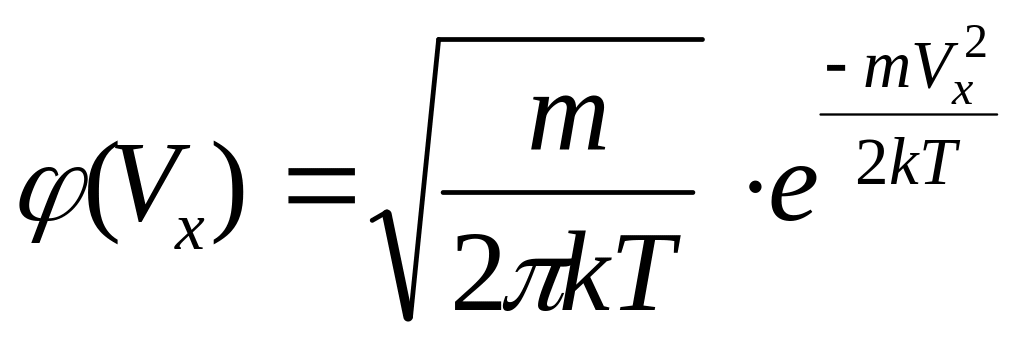
— масса молекул.

— температура газа.

— проекция скорости молекулы.

— постоянная Больцмана.

11. Распределение Максвелла для величины скорости молекул

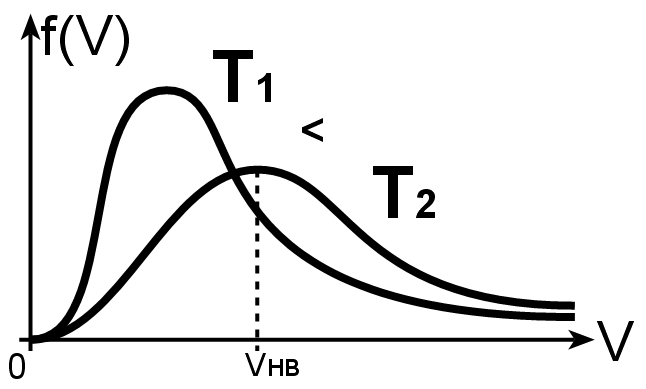
— масса молекул.

— температура газа.

—скорости молекулы.

— постоянная Больцмана.

12. Распределения Максвелла для кинетической энергии молекул

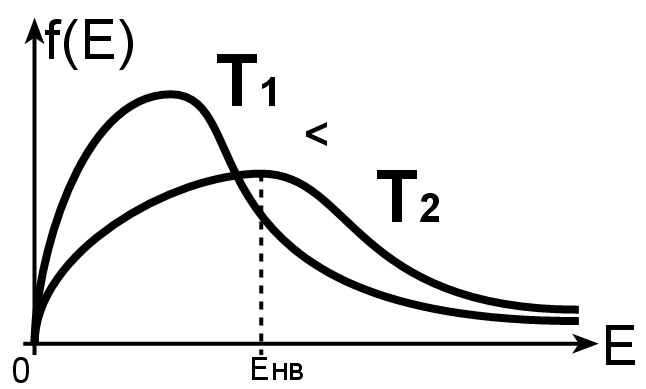
— температура газа.

—кинетическая энергия молекулы.

— постоянная Больцмана.

13. Первое начало термодинамики

Теплота, сообщённая телу, равна сумме изменения внутренней энергии тела и работы, которую совершает тело над внешними телами.

— работа, совершаемая телом над внешними телами.

— теплота, сообщаемая телу.

— изменение внутренней энергии тела.

14. Определение теплоемкости тела. Что такое удельная и молярная теплоемкости?

Теплоёмкость тела - количество теплоты, которое нужно сообщить телу, чтобы изменить его температуру на .

Удельная теплоёмкость — теплоёмкость единицы массы данного вещества:

, где — масса данного вещества.

Молярная теплоёмкость — теплоёмкость 1 моля данного вещества:

, где — молярная масса.

15. Уравнение Майера

Уравнение Майера показывает соотношение между молярной теплоёмкостью при постоянном давлении и постоянном объёме:

— масса молекулы.

— молярная масса.

— молярная теплоёмкость при постоянном давлении.

— молярная теплоёмкость при постоянном объёме.

— универсальная газовая постоянная.

16. Что такое энтропия? Статистическая и термодинамическая формулировки

• Статистический подход

Энтропия — функция состояния, т.е. энтропия не зависит от того, как система попала в данное состояние.

— постоянная Больцмана.

— число квантовых состояний, соответствующих данному значению энергии (статистический вес).

• Термодинамический подход

Изменение энтропии термодинамической системы при обратимом процессе равно отношению общего количества тепла к величине абсолютной температуры.

— абсолютная температура.

— теплота, сообщённая системе при обратимом процессе.