17. Свободная энергия Геймгольца

Энтропия является критерием оценки в направлении протекании системы. На практике рассматриваются системы закрытые и открытые для таких систем вводятся новые функции состояния рассмотрим закрытые системы.

V,T изохорно изотермический

dU=əQ - əW əQ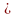 TdS dU TdS - əW əW - dU+ TdS

əW - d(U-TS) F=U-TS əW - dF

F – изохорноизотермический потенциал или свободная энергия Гейм-Гольца. Эта часть внутренней энергии которая может быть превращена в работу.

А) əW= - dF

-

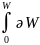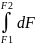
Б) əW< - dF максимальная работа которая может совершаться в изолированном процессе

dF= dU - TdS ΔF=ΔU - TdS

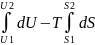= W_V - ΔF

В закрытых системах находящихся в изохорноизотермических условиях самопроизвольно могут протекать процессы, которые сопровождаются свободной энергией Гейм-Гольца причём пределом их протекания тоесть условием равновесия является достижение некоторого минимального значенияпри данных условиях

А) ΔF < 0 Б) ΔF=0

Таким образом свободная энергия Гейм-Гольца является критерий напр. проц. в закрытой системах. Определим зависимость свободной энергии Г-Г от термодинамических параметров.

dF=(əQ/əV)_TdV + (əF/əT)_VdT (1)

dF=dU – TdS – SdT (2)

dU=TdS – pdV (3)

Решим совмесно уровнение (2) и (3)

dF= - pdV – SdT (4)

Сопоставим уравнение (1) и (4)

(əF/əV)_T= - p

(əF/əT)= - S (5)

Из формулы (5) => энтропия является мерой убыли свободы Г-Г при нагревании в условиях постоянного объёма.

А давление мерой убыли свободной энергии Г-Г с ростом V при постоянной Т.

18.Свободная энергая Гиббса

Близкой к изохорно изотермическому потенциалу в условиях постоянного давления и температуры является изобарно изотермический потенциал или свободная энергия Гиббса.

p,T=const

əQ=dU+pdV TdS – dU – pdV=0 d(TS – U – pV)=0 d(U – pV – TS)=0 d(F – pV)=0

G=F+pV и з о б а р н о и з о т е р м и ч е с к и й п о т е н ц и а л

Изобарно изотермический потенциал является полным дифференциалом функции значение которой = 0

G= F + pV G= - W_p F = - W_V W_P – максимальная полезная работа которая может совершаться в изотермических условиях

ΔG= ΔF + pΔV

W_P=W_V – pΔV максимальная полезная работа=максимальной работе W_V за вычетом работы против внешнего давления.

W_P ΔG

В системах находятся при постоянном давлении и температуре, самопроизвольно могут протекать процессы которые сопровождаются уменьшением свободной энергией Гиббса причём пределом их протекания является достаточно некоторое минимальное значение

ΔG<0 ΔG=0 система находится в состоянии равновесия

G=f(p,T)

dG=(əG/əp)_Tdp+(əG/əT)_TdT

G=U – TS + pV

dG=dU – TdS – SdT +pdV+Vdp

dU=TdS – pdV

dG=TdS – pdV – TdS – SdT +pdV +Vdp

dG= - SdT +Vdp (2)

Решим совмесно уровнения (2) и (1)

(əG/əT)_P= - S

(əG/əT)_T=V (3)

Из выражения (3) => что энтропия мера убыли свободной энергии Гиббса при изобарном нагревании системы (p=const), а объём мера воздействия свободной энергии Гиббса при изотермическом повышении давлении (Т=const)/