Лабораторная работа № 12

ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИИ В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ

Цель работы: изучение вынужденных колебаний в электрическом контуре и определение параметров контура.

1. Теория

В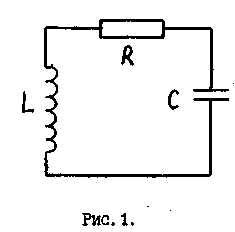 ынужденными называются колебания, в процессе которых система подвергается внешнему периодически изменяющемуся воздействию. В конкретном случае электрического колеба­тельного контура это означает, подключе­ние к контуру внешней электродвижущей си­лы ε периодически изменяющейся со вре­менем и создающей в контуре переменное электрическое напряжение (рис.1). Следо­вательно, уравнение Кирхгофа (закон Ома для неоднородного участка цепи) с учетом внешней ЭДС ε и ЭДС самоиндукции имеет вид (см. лаб. работу 12а):

(1)

где ток , напряжение , q - заряд на обкладках конденсатора, t - время, С - емкость конденсатора, R. - сопротивление, L - индуктивность контура. Разделив (1) на L, получаем:

(2) С учетом обозначений собственная частота колебаний перепишем (2) в виде:

(3)

Рассмотрим колебательный процесс в контуре, к которому подключена внешняя ЭДС , зависящая от времени по гармоническому зако­ну:

(4)

на основе решения полного уравнения (3) с учетом (4). Частное ре­шение этого уравнения имеет вид

(5)

где

;

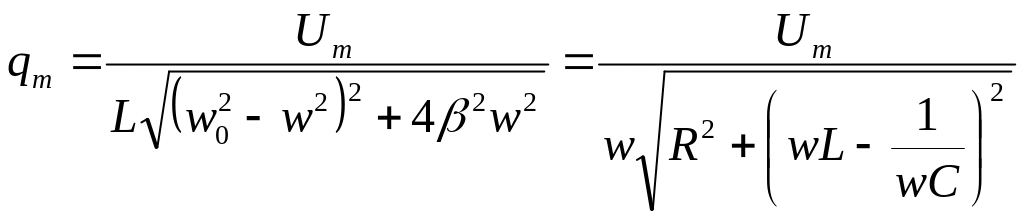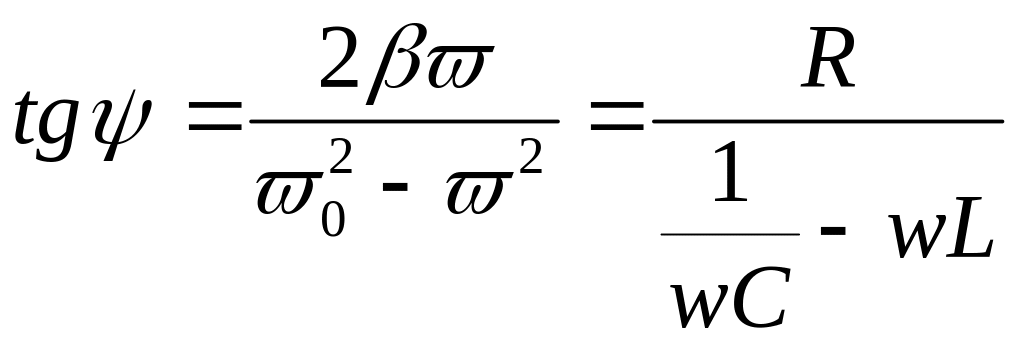
Общее решение (3) получится, если к данному частному решению прибавить общее решение соответствующего однородного уравнения (т.е. уравнения (3) с нулевой правой частью). Это решение получено в лабораторной работе N 12а и содержит экспоненциальный множитель , поэтому с течением времени это слагаемое становится очень малым и им можно пренебречь. Следовательно, установившиеся вынужденные колебания описываются функцией (5). Напряжение на конденсаторе равно

(6)

т.е. вынужденные колебания происходят с частотой равной частоте внешней ЭДС, а амплитуда колебаний зависит от этой частоты. Резонансная частота w_pqдля заряда q и напряжения на конденсаторе U ( w_pu ) находится из минимум* выражения, стоящего под корнем в знаменателе для q_m и равна:

(7)

Резонансные кривые для U изображены на рис 2а. При W→0 кри­вые сходятся в одной точке с ординатой U_m , равной напряжению, воз­никающему на конденсаторе при подключении его к источнику постоянного напряжения U_m . Макcимум при резонансе получается тем вы­ше и острее, чем меньше , т. е. Чем меньше активное сопротивление R и больше индуктивность L контура.

Собственно резонансом называется резкое возрастание амплитуды колебаний при совпадении частоты внешнего генератора с собственной частотой колебаний в контуре.

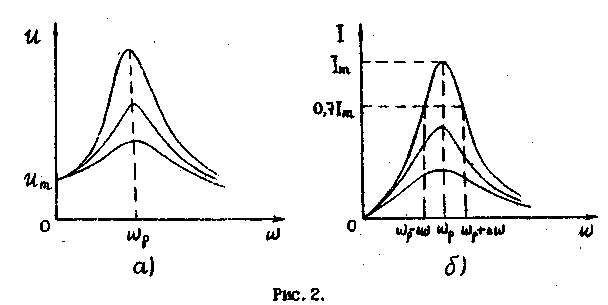
График зависимости амплитуды колебаний от частоты внешней ЭДС называют резонансной кривой. Пик на резонансной кривой, соответст­вующий частоте w_p , указывает на наступление резонанса. Величина активного сопротивления контура К. определяет максимальное значе­ние тока в контуре при наступлении резонанса. На графике это про­является в изменении высоты и остроты "пика" на резонансной кри­вой. Конкретный вид резонансной кривой, т. е. зависимость амплитуды вынужденных колебаний от частоты внешней ЭДО, определяет как быстро в контуре происходит затухание колебаний, имеющих частоту, отличающуюся от резонансной. Сила тока в контуре при установивших­ся колебаниях равна (8) где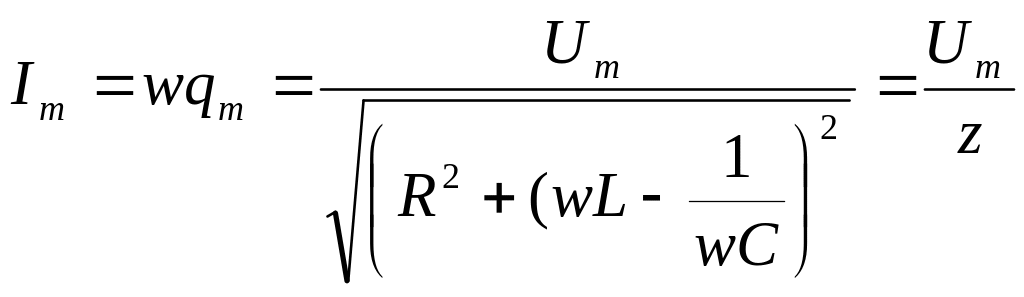 - амплитуда тока, а

выражение - называется полным электрическим сопротивлением или импедансом. Максимальное значение амплитуды тока достигается при условии . Следовательно, резонансная частота для силы тока w_pi совпадает с собственной часто­той контура w₀:

(9)

Отрезок, отсекаемый резонансными кривыми на оси I_m , равен нулю (при w=О , I_m⁼Ο ), поскольку при постоянном напряжении установившийся ток в цепи с конденсатором течь не может. Резонансные кривые для силы тока изображены на рис. 26. Чем уме ре­зонансная кривая, тем выше избирательность колебательного контура, т. е. способность контура выделить определенную частоту из многих сигналов различной частоты. Избирательность контура принято харак­теризовать полосой пропускания. Под полосой пропускания контура понимает ширину резонансной кривой, выраженную в Герцах и опреде­ленную по уровню 0,7 от максимальной амплитуды колебаний (см. рис.2). Следует отметить, что добротность контура может быть опре­делена по виду резонансной кривой по формуле:

(10)

где w_р - резонансная частота, 2Δω - полоса пропускания контура.