1. Понятие матрицы. Виды матриц. Алгебраические операции над матрицами (умножение на число, сложение, умножение матриц) и их свойства. Транспонирование матрицы. Свойства транспонирования матрицы.

О пределение. Матрицей размера   называется прямоугольная таблица, содержащая m строк и n столбцов.

Матрицы широко применяются для описания экономических объектов и процессов. Элементами матрицы могут быть числа, буквы (символы) и другие объекты.

Матрицы обозначают прописными (заглавными) буквами A, B, C, …, элементы матрицы – строчными буквами с двойной индексацией aij, где i - номер строки, j - номер столбца:

Виды матриц:

1) Матрица-строка:  ;

2) Матрица-столбец:  ;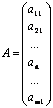 

3) Нулевая матрица:  ;

4) Квадратная матрица – если  (например n = 2):  ;

5) Диагональная матрица (напр. 3-го порядка, где   любые числа  ):  ;

6) Единичная матрица (например, 3-го порядка) 

Операции над матрицами

1. Умножение матрицы на число.

Произведением матрицы A на число называется матрица  ,элементы которой  для

Пример. Вычислить  , если  .    Р е ш е н и е:   .

Если  , то   (нулевая матрица того же размера).

2.       Сложение матриц.

Суммой матриц   и   одинакового размера   называется матрица  , элементы которой   для 

Пример. Вычислить С = А + В, если  .

  Р е ш е н и е:  .

3.       Вычитание матриц.

Разность матриц одинакового размера определяется как  .

4.       Умножение матриц.

Умножение матрицы   на матрицу   определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц   называется матрица  , каждый элемент которой   равен сумме произведений элементов  -ой строки матрицы   на соответствующие элементы  -го столбца матрицы  :

, где 

Пример. Вычислить произведение матриц  , где  ,  .

Р е ш е н и е.

Найдем размер матрицы произведения  , следовательно, умножение возможно.

= .

Свойства операций сложения и умножения матриц

1)        .                                                             5)  .

2)        .                                         6)  .

3)        .                                                     7)  .

4)        .

8)   (в общем случае). Кроме того, если   существует, то   может вообще не существовать.

9)  , где   - единичная квадратная матрица.

10) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. если  , то не следует, что   или  .

Пример.  ,  , но  .

5. Возведение в степень.

Целой положительной степенью   квадратной матрицы  называют произведение  матриц, равных , т.е.  .

6. Транспонирование матриц.

Транспонирование матрицы есть переход матрицы   к матрице  , в которой строки и столбцы поменялись местами с сохранением порядка.

,  ,

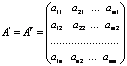т.е. если   имеет размер  , то   имеет размер  .

Свойства операции транспонирования.

1)              .                                  3)      .

2)              .                                          4)      .

2. Понятие определителя n-ого порядка. Основные свойства определителей.

Пусть дана квадратная таблица, состоящая из чисел, расположенных в n горизонтальных и в nвертикальных рядах. С помощью этих чисел по определённым правилам вычисляют некоторое число, которое называют определителем n-го порядка и обозначают следующим образом:

                    (1)

Горизонтальные ряды в определителе (1) называют строками, вертикальные – столбцами, числа  -элементами определителя (первый индекс означает номер строки, второй – номер столбца, на пересечении которых стоит элемент; i = 1, 2, ..., n;  j = 1, 2, ..., n). Порядок определителя – это число его строк и столбцов.

Воображаемая прямая, соединяющая элементы определителя, у которых оба индекса одинаковы, т.е. элементы

называется главной диагональю, другая диагональ – побочной.

Определителем n-го порядка называется число, являющееся алгебраической суммой n! членов, каждый из которых – произведение n его элементов, взятых только по одному из каждой n строк и из каждого nстолбцов квадратной таблицы чисел, причём половина (определённых) членов берётся с их знаками, а остальные – с противоположными.

Покажем, как вычисляются определители первых трёх порядков.

Определитель первого порядка – это сам элемент   т.е.

 .

Определитель второго порядка есть число, получаемое следующим образом:

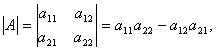                   (2) где

- элементы определителя, а

и 

- его члены.

Равенство (2) показывает, что со своим знаком берётся член, являющийся произведением элементов главной диагонали, а с противоположным – член, представляющий собой произведение элементов противоположной диагонали.

Свойство 1. При замене строк столбцами (транспонировании) значение определителя не изменится, т.е.

Свойство 2. Если хотя бы один ряд (строка или столбец) состоит из нулей, то определитель равен нулю. Доказательство очевидно.

В самом деле, тогда в каждом члене определителя один из множителей будет нуль.

Свойство 3. Если в определителе поменять местами два соседних параллельных ряда (строки или столбцы), то определитель поменяет знак на противоположный, т.е.

 

Свойство 4. Если в определителе имеются два одинаковых параллельных ряда, то определитель равен нулю:

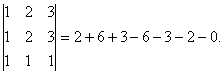
Свойство 5. Если в определителе два параллельных ряда пропорциональны, то определитель равен нулю:

Свойство 6. Если все элементы определителя, стоящие в одном ряду, умножить на одно и то же число, то значение определителя изменится в это число раз:

Следствие. Общий множитель, содержащийся во всех элементах одного ряда, можно вынести за знак определителя, например:

 

Свойство 7. Если в определителе все элементы одного ряда представлены в виде суммы двух слагаемых, то он равен сумме двух определителей:

Свойство 8. Если к элементам какого-либо ряда прибавить произведение соответствующих элементов параллельного ряда на постоянный множитель, то значение определителя не изменится:

Свойство 9. Если к элементам i-го ряда прибавить линейную комбинацию соответствующих элементов нескольких параллельных рядов, то значение определителя не изменится:

Справедливость этого равенства вытекает из свойства 8.

 

3. Миноры и алгебраические дополнения. Теорема о разложении определителя по элементам строки и столбца. Теорема о сумме произведений элементов какой-либо строки определителя на алгебраические дополнения соответствующих элементов другой строки.

   Минор

Минором   элемента   матрицы  n-го  порядка называется определитель матрицы  (n-1)-го порядка, полученный из матрицы  А  вычеркиванием  i-й строки и  j-го столбца.

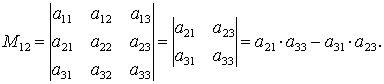
При выписывании определителя  (n-1)-го порядка, в исходном определителе элементы находящиеся под линиями в расчет не принимаются.

Пример 1. Составить минор  , полученную из исходной матрицы:

Решение:

.