
- •3 Аттестация. Смысл параметров канонического распределения.
- •Парадокс Гиббса.
- •Распределение Максвелла-Больцмана. Распределение Максвелла и распределение Больцмана.
- •Распределение Максвелла.
- •Распределение Больцмана.
- •Теорема о равномерном распределении кинетической энергии по степеням свободы и теорема о «вириале».
- •Теорема о вириале.
- •Следствие из теоремы о вириале.
- •Большое каноническое распределение.
- •Квантовое распределение.
Теорема о вириале.
Если обобщённая координата равна обобщённой переменной , то согласно равенству (1):

Величину
под знаком среднего
 Клаузис назвал вириалом.
Клаузис назвал вириалом.
Теорема: на одну степень свободы в среднем приходится вириал равный .
Следствие из теоремы о вириале.
Если от какой-то координаты потенциальная энергия зависит только квадратичным образом, то на соответствующую степень свободы в среднем приходится энергия .
Доказательство:

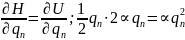
Т.е. среднее
от величины
 равно
равно

Значит на степень свободы n , будет приходится .
Пример 1: Если нужно подсчитать среднюю энергию идеального одноатомного газа.


Нестандартным способом:



Пример 2: Необходимо подсчитать энергию системы N-линейных гармонических осцилляторов:

 переходим к сумме средних, тогда:
переходим к сумме средних, тогда:

Большое каноническое распределение.
Каноническое распределение Гиббса описывает изотермические системы с постоянным числом частиц. Но число частиц в системе не всегда постоянно:
Если идёт медленная химическая реакция;
Если происходят фазовые переходы, т.е. сопровождающие изменение фазового состояния.
В случае излучения (фотонный газ).
В данном случае необходимо уточнить (когда число частиц меняется) основное уравнение термодинамики, т.к. энергия при изменении числа частиц в системе изменяется.

Энергия
системы может изменятся за счёт:
теплообмена
 ,
совершения работы
,
совершения работы
 ,
изменения числа частиц
,
изменения числа частиц

 - химический потенциал. Физический смысл
химического потенциала: численно равен
энергии на которую изменится энергия
системы при добавлении одной частицы
(учитывается потенциальная энергия
взаимодействия с другими частицами).
- химический потенциал. Физический смысл
химического потенциала: численно равен
энергии на которую изменится энергия
системы при добавлении одной частицы
(учитывается потенциальная энергия
взаимодействия с другими частицами).
Первое определение химического потенциала:


Второе определение химического потенциала:



Из эксперимента
известно, что термодинамический потенциал
 является аддитивной функцией.
является аддитивной функцией.

 ,
где
,
где
 – удельная энтропия,
– удельная энтропия,
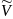 - удельный объём.
- удельный объём.

 Раскрывают термодинамический
смысл химического потенциала.
Раскрывают термодинамический
смысл химического потенциала.
 Можно получить выражение для свободной
энергии
Можно получить выражение для свободной
энергии


Раскрывают смысл большого термодинамического потенциала.
Т.к. система изотермическая, мы можем воспользоваться каноническим распределением. Но только для конкретного момента времени с фиксированным числом частиц. Оно не будет носить универсального характера, т.к. число частиц в системе изменяется. Пусть в момент времени t число частиц в системе N:

Если момент времени t’ и число частиц N’, то:


 ;
;
 - само распределение (большое каноническое
распределение).
- само распределение (большое каноническое
распределение).
Число частиц N – не параметр, а переменная величина;
Условием нормировки большого канонического распределения является следующие условия:

Если число частиц, которые Вы возьмёте не совпадёт с числом частиц в системе, то вместо 1 получится 0.
Тогда, если просуммировать:


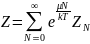
Где
 – интеграл состояния
– интеграл состояния

Для энергии системы:

Основной
расчётной характеристикой является
большая
статистическая сумма,
которая даёт выражение для большого
термодинамического потенциала
 .
.
Квантовое распределение.
При нахождении фазового объёма и интеграла состояний, мы учитываем квантово-механические принципы – принцип неопределённости и принцип тождественности. Но тем не менее рассмотренные ранее распределения являются классическими, несмотря на то, что система, состоящая из молекул, атомов, ионов и т.п., является чисто квантовой. Мы имеем возможность получить и использовать для них классические распределения только для высоких температур.
Вводится
понятие характеристической температуры
 и при температуре
и при температуре
 можно пользоваться распределением. А
при
можно пользоваться распределением. А
при
 даёт результат совершенно не согласующийся
с экспериментом. Т.е. экспериментальное
значение стремится к нулю.
даёт результат совершенно не согласующийся
с экспериментом. Т.е. экспериментальное
значение стремится к нулю.
Учитывая,
что квантовый случай – и рассматривая
изотермическую систему, мы должны
функцию Гамильтона заменить на оператор
Гамильтона:
 .
.
Решение уравнения Шрёдингера для которого считаем известным:

Соответственно,
 становится матрицей, т.е.
становится матрицей, т.е.

Далее найдём матричные элементы этой матрицы:

Если
вместо
 :
:
 ,
тогда:
,
тогда:

Теперь


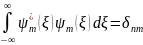
Т.к собственные
функции оператора
всегда являются ортонормированными,
то интеграл, который даст при n
и m – одинаковых 1,
а при не равных 0. Т.е. делаем вывод:

Вывод: матрица является диагональной:
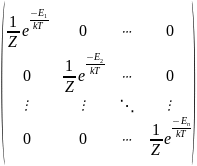
Т.к. квантовые
состояния часто бывают вырожденными,
т.е. одному значению энергии может
соответствовать несколько волновых
функций
 (т.е. несколько состояний), а квантовое
распределение даёт вероятность данного
значения энергии, которое с учётом
кратности вырождения должна быть больше.
(т.е. несколько состояний), а квантовое
распределение даёт вероятность данного
значения энергии, которое с учётом
кратности вырождения должна быть больше.
Условие
нормировки квантового распределения:


n – номер энергетического состояния.
Статистическая
сумма:

и т.п.
