Распределение Максвелла-Больцмана. Распределение Максвелла и распределение Больцмана.

Рассмотрим изотермическую систему – идеальный газ. Для простоты будем считать его одноатомным. Это значит, что функцию Гамильтона мы можем представить в виде

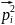
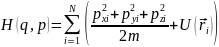
В общем случае:

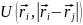
Потенциальная энергия зависит как и от координаты отдельной частицы, так и от взаимного расположения их относительно друг друга. Но в случае идеального газа, когда между частицами нет взаимодействия и на каждую частицу действуют только внешние поля, то потенциальная энергия зависит только от координаты.

Это значит, что функция Гамильтона в данном случае становится аддитивной функцией, т.к. теперь потенциальная энергия является аддитивной функцией, а кинетическая является таковой (аддитивной) всегда.

С учётом того, что T=const, воспользуемся каноническим распределением.

Таким образом, в случае идеального газа, каноническое распределение представляется в виде произведения так называемых одночастичных распределений, т.е. каждая из которых зависит от координат и импульсов отдельной (конкретной) частицы. Значит частицы являются статистически независимыми. Соответствующее распределение называется распределением Максвелла-Больцмана.

По поведению одной частицы (в системе невзаимодействующих частиц) мы можем судить о поведении системы в целом.

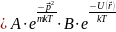
Распределение Максвелла. Распределение Больцмана.

Распределение Максвелла.

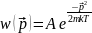
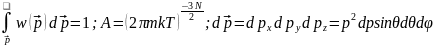
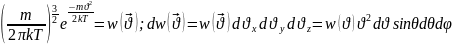
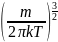– нормировочная константа, которая находится из условия нормировки.

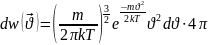
Если нас не интересует выделенное направление, а только модуль:

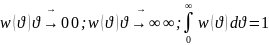
Вид распределения:

Если смещается влево, то больше; если вправо, то меньше.

Распределение Больцмана.

Условие нормировки:

Явный вид нормировочной константы B можно найти только, если мы знаем вид потенциальной энергии. (т.е. уже для каждого конкретного случая).

Распределение Больцмана имеет много приложений. В частности с помощью него можно получить «барометрическую» формулу (она определяет атмосферное давление в зависимости от высоты). Давление пропорционально концентрации частиц.

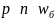(концентрация описывается распределением Больцмана).

Для давления аналогичная формула

Теорема о равномерном распределении кинетической энергии по степеням свободы и теорема о «вириале».

В случае изотермической системы с постоянным числом частиц найдём статистическое среднее:

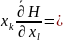, где под x будем понимать любую обобщённую переменную.

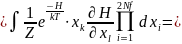
. Нужно подсчитать этот интеграл. Разобьём его на две части.

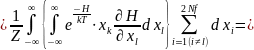
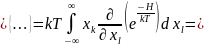
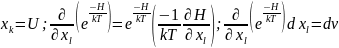
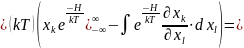
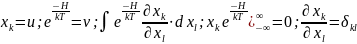
В первом слагаемом пределы подставляем вместо 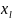в функцию Гамильтона. Если является обобщённой координатой, она войдёт в потенциальную энергию:

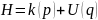
Т.к. мы использовали каноническое распределение это значит, что мы считаем систему равновесной. Это значит, что объём системы должен быть ограничен. Это значит, что потенциальная энергия на стенках сосуда имеет бесконечно большое значение. Т.к. мы поставили бесконечные пределы, то потенциальная энергия 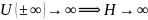,а функция Гамильтона

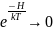
Если – обобщённый импульс 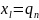, т.е. 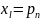, то кинетическая энергия:

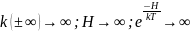, поэтому

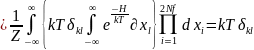
Рассмотрим случай, когда k=l, тогда (символ Кроникера).

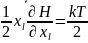(1)

То, что относится к теореме о кинетической энергии.

Если (обобщённый импульс), то воспользуемся равенством (1):

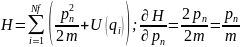
(т.е. зависимость только через кинетическую энергию).

Получаем: Т.к. n может принимать любое положительное значение от 1 до Nf. Это означает, что на каждую степень свободы системы в среднем будет приходится энергия равная , где k – постоянная Больцмана.