3 Аттестация. Смысл параметров канонического распределения.
Каноническое
распределение :
(1)
От q и p не
зависит
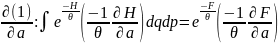домножим левую и правую части на
Получаем в левой части
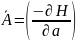или
(2)
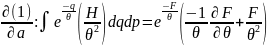домножим обе части на
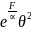
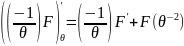
Среднее значение функции Гамильтона Энергия системы (или внутренняя энергия)
(3)
Параметр
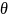обладает смыслом температуры (т.е.
величина, пропорциональная температуре).
Это можно доказать двумя способами:
Доказательство (физическое):
Рассмотрим две
адиабатически изолированные равновесные
системы
и
Пусть 1-ая система характеризуется
параметром
,
а 2-я система параметром
.
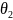Приведём эти две системы в тепловой
контакт и рассмотрим образовавшуюся
систему
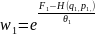
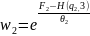
В силу статистической
независимости подсистемы
! Будет ли новое распределение w равновесным?
;
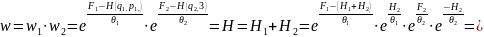
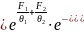
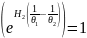
Если показатель равен
нулю, то
.
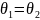Согласно нулевому началу термодинамики, две адиабатически изолированные равновесные системы образуют при приведении их в тепловой контакт образуют равновесную систему, только при условии равенства температур исходных систем. В нашем случае при условии равенства очевидно обладает смыслом температуры.
Доказательство (математическое):
Покажем, что множитель
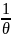является интегрирующем множеством для
,
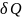т.е
(при интегрировании по замкнутому
контуру)
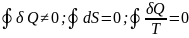
Для этого воспользуемся
равенством (3):
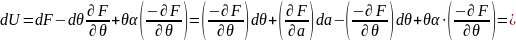
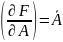
Мы доказали, что и
требовалось
;
k –коэффициент
пропорциональности.
Воспользуемся
равенством (3):
Т.е. Вывод: F
– свободная энергия. Из уравнения (3):
Формулы:
– Интеграл состояния (основная расчётная
характеристика, находится из
соответствующей нормировки).
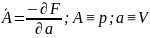
Парадокс Гиббса.
Рассмотрим изотермическую систему из N частиц в объёме V при температуре T. Для простоты будем считать систему идеальным одноатомным газом в отсутствии внешних полей. Интеграл состояния такой системы:
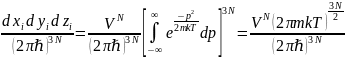
получаем:
при условии, что k –
постоянная Больцмана.
Т.е. вычислив давление и получив уравнение состояния мы доказали, что k не просто константа, а постоянная Больцмана, и показали, согласие теории с экспериментами.
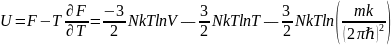
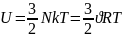
Свободная энергия и энтропия в случае идеального газа являются аддитивными функциями – это экспериментальный факт. Проверим, будет ли выполнятся это условие:
Увеличим
число частиц в системе и объём в
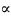раз.
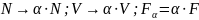
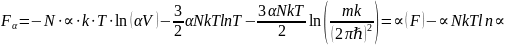
Мы нашли свободную энергию и показали, что она не является аддитивной функцией, хотя должна была. В этом и состоит парадокс Гиббса. Каноническое распределение является правильным, и исходя из результатов полученных для давления и энергии, но даёт неправильный результат для свободной энергии и энтропии.
! Разрешить этот парадокс Гиббс предложил формально. Фазовый объём и соответствующий интеграл состояния Гиббс предложил разделить на (N!):
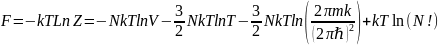
Воспользуемся формулой Стирлинга. При N>>1 (т.к. система макроскопическая):
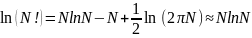
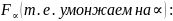
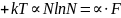
Объяснить почему нужно делить на N! Смогли спустя много-много лет. А именно только тогда, когда был сформулирован квантово-механический принцип воздействия. В таких системах тождественность частиц реализует только такие состояния, которые не учитываются при перестановки частиц.
Если движение частиц описывается классическими движениями, что для частиц используется понятие траектории. Т.е. при движении частиц проследить каким образом она двигалась и в какую точку попала.
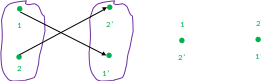
В случае, когда поменялись местами две частицы, то это можно обнаружить.
Если частицы подчиняются квантовым законам, то задавать траекторию их движения невозможно – из-за состояния неопределённости. Значит когда две частицы просто поменялись местами, это не будет новым состоянием.
Т.к. в системе N частиц, то число таких перестановок равно N!. Значит число состояний системы необходимо уменьшить в N! раз, т.к. в фазовом пространстве число возможных состояний изображается в виде фазового объёма, его необходимо уменьшить в N! раз.
