6.5. Многоканальная смо с ограниченной длиной очереди

Рассмотрим многоканальную СМО ( ), на вход которой поступает пуассоновский поток заявок с интенсивностью , a интенсивность обслуживания каждого канала составляет , максимально возможное число мест в очереди ограничено величиной . Дискретные состояния СМО определяются количеством заявок, поступивших в систему, которые можно записать.

Пока СМО находится в любом из этих состояний - очереди нет. После того как заняты все каналы обслуживания, последующие заявки образуют очередь, тем самым определяя дальнейшее состояние системы:

Граф состояний -канальной СМО с очередью, ограниченной местами, представлен на рис. 6.6.

Рис. 6.6. Граф состояний -канальной СМО

с ограничением на длину очереди

Переход СМО в состояние с большими номерами определяется потоком поступающих заявок с интенсивностью , тогда как по условию в обслуживании этих заявок принимают участие одинаковых каналов с интенсивностью потока обслуживания равного для каждого канала. При этом полная интенсивность потока обслуживания возрастает с подключением новых каналов вплоть до такого состояния , когда все каналов окажутся занятыми. С появлением очереди интенсивность обслуживания более не увеличивается, так как она уже достигла максимального значения, равного .

Запишем выражения для предельных вероятностей состояний:

Выражение для можно преобразовать, используя формулу геометрической прогрессии для суммы членов со знаменателем :

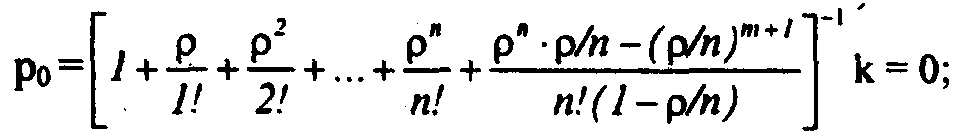
Образование очереди возможно, когда вновь поступившая заявка застанет в системе не менее требований, т.е. когда в системе будет находиться , , ,…, требований. Эти события независимы, поэтому вероятность того, что все каналы заняты, равна сумме соответствующих вероятностей , , , …, . Поэтому вероятность образования очереди равна:

Вероятность отказа в обслуживании наступает тогда, когда все каналов и все мест в очереди заняты:

Относительная пропускная способность будет равна:

абсолютная пропускная способность -

среднее число занятых каналов -

среднее число простаивающих каналов -

коэффициент занятости (использования) каналов -

коэффициент простоя каналов -

среднее число заявок, находящихся в очередях, -

в случае, если эта формула принимает другой вид -

среднее время ожидания в очереди определяется выражениями, называемыми формулами Литтла -

Среднее время пребывания заявки в СМО, как и для одноканальной СМО, больше среднего времени ожидания в очереди на среднее время обслуживания, равное , поскольку заявка всегда обслуживается только одним каналом:

Пример 1. В мини-маркет поступает поток покупателей с интенсивностью 6 покупателей в 1 мин, которых обслуживают три контролера-кассира с интенсивностью 2 покупателя в 1 мин. Длина очереди ограничена 5 покупателями. Определим характеристики СМО и дадим оценку ее работы.

Решение.

находим предельные вероятности состояний СМО:

доля времени простоя контролеров-кассиров -

вероятность того, что занят обслуживанием только один канал-

вероятность того, что заняты обслуживанием два канала -

вероятность того, что заняты обслуживанием все три канала -

вероятность того, что заняты обслуживанием все три канала и пять мест в очереди -

Очевидно, что . Вероятность отказа наступает при и составляет .

Относительная и абсолютная пропускные способности СМО соответственно равны и (покупателя в 1 мин).

Среднее число занятых каналов и средняя длина очереди равны:

Среднее время ожидания в очереди и пребывания в СМО соответственно равно: мин, мин.

Таким образом, увеличение числа касс с трех до четырех позволяет существенно улучшить эффективность работы СМО: отказа в обслуживании не получает ни один покупатель, уменьшаются средняя длина очереди и среднее время пребывания покупателей в СМО.

Пример 2. На плодоовощную базу в среднем через 30 мин прибывают автомашины с плодоовощной продукцией. Среднее время разгрузки одной машины составляет 1,5 ч. Разгрузку производят две бригады грузчиков. На территории базы у дебаркадера могут находиться в очереди в ожидании разгрузки не более 4 автомашин. Определим показатели и дадим оценку работы СМО.

Решение.

СМО двухканальная, с ограниченным числом мест в очереди , интенсивность входящего потока авт/ч, интенсивность обслуживания авт/ч, интенсивность нагрузки , .

Определяем характеристики СМО:

вероятность того, что все бригады не загружены, когда нет автомашин -

вероятность отказа, когда под разгрузкой два автомобиля, а в очереди четыре автомобиля -

относительная пропускная способность или вероятность обслуживания -

абсолютная пропускная способность -

среднее число занятых бригад -

коэффициент занятости работой бригад грузчиков -

среднее число автомашин в очереди -

Доля времени простоя грузчиков очень мала и составляет всего 1,58% рабочего времени, а вероятность отказа велика: 36% заявок из числа поступивших получают отказ в разгрузке, обе бригады практически заняты полностью, коэффициент занятости близок к единице и равен 0,96, относительная пропускная способность мала - всего 64% из числа поступивших заявок будут обслужены, средняя длина очереди 2,6 автомашины, следовательно, СМО не справляется с выполнением заявок на обслуживание и необходимо увеличить число бригад грузчиков и шире использовать возможности дебаркадера.

Пример 3. Коммерческая фирма получает по кольцевому завозу ранние овощи из теплиц пригородного совхоза в случайные моменты времени с интенсивностью 6 единиц в день. Подсобные помещения, оборудование и трудовые ресурсы позволяют обработать и хранить продукцию в объеме двух единиц. На фирме работают 4 человека, каждый из которых в среднем может обработать продукцию одного завоза в течение 4 ч. Продолжительность рабочего дня при сменной работе составляет 12 ч. Какова должна быть емкость складского помещения, чтобы полная обработка продукции была бы не менее 97% из числа осуществляемых поставок?

Решение.

Решим задачу путем последовательного определения показателей СМО для различных значений емкости складского помещения и т.д. и сравнения на каждом этапе расчетов вероятности обслуживания с заданной величиной .

Определяем интенсивность нагрузки:

Находим вероятность или долю времени простоя для

Вероятность отказа в обслуживании, или доля потерянных заявок, -

Вероятность обслуживания, или доля обслуженных заявок из числа поступивших, составляет:

Поскольку полученная величина меньше заданной величины 0,97, то продолжаем вычисления для . Для этой величины показатели состояний СМО имеют значения:

Вероятность обслуживания и в этом случае меньше заданной величины, поэтому продолжаем вычисления для следующего , для которого показатели состояния имеют такие значения: ; ; . Теперь полученная величина вероятности обслуживания удовлетворяет условию задачи, поскольку 0,972 > 0,97, следовательно, емкость складского помещения необходимо увеличить до объема 4 единиц.

Для достижения заданной вероятности обслуживания можно подобрать таким же образом оптимальное количество человек на обработке овощей, проводя последовательно вычисления показателей СМО для и т.д. Компромиссный вариант решения можно найти путем сравнения и сопоставления для разных вариантов организаций СМО затрат, связанных как с увеличением числа работающих, так и созданием специального технологического оборудования по обработке овощей на коммерческом предприятии.

Такими образом, модели массового обслуживания в сочетании с экономическими методами постановки задач позволяют проводить анализ существующих СМО, разрабатывать рекомендации по их реорганизации для повышения эффективности работы, а также определять оптимальные показатели вновь создаваемых СМО.

Пример 4. На автомойку в среднем за час приезжают 9 автомобилей, но если в очереди уже находятся 4 автомобиля, вновь подъезжающие клиенты, как правило, не встают в очередь, а проезжают мимо. Среднее время мойки автомобиля составляет 20 мин, а мест для мойки всего два. Средняя стоимость мойки автомобиля составляет 70 руб. Определите среднюю величину потери выручки автомойки в течение дня.

Решение.

Находим интенсивность нагрузки:

Определяем долю времени простоя автомойки:

вероятность отказа -

Относительная пропускная способность равна:

Абсолютная пропускная способность:

Среднее число автомобилей в очереди:

Среднее число заявок, находящихся в обслуживании:

Среднее время ожидания в очереди:

Среднее время пребывания автомашины на мойке:

Таким образом, из числа поступивших заявок 34% не будут обслужены, следовательно, за 12 ч работы одного дня потеря выручки автомойки составит в среднем .