36)Понятие первообразной и неопределённого интеграла.
Определение 1: Функция F(x) называется первообразной функцией для данной функции f(x), если для любого x из области определения f(x)выполняется равенство F'(x)= f(x) или dF(x)= f(x)dx
Определение 2: Множество F(x) + C всех первообразных функций для данной функции f (x) , где C принимает все возможные числовые значения, называется неопределенным интегралом от функции f (x) и обозначается символом
Таким образом, по определению,
где F'(x)
= f (x) или dF(x)
= f(x)dx и С -
произвольная постоянная. В последней
формуле f(x) называется подинтегральной
функцией, f(x)dx -подинтегральным
выражением,
а символ 
-
знаком неопределенного
интеграла.
Неопределенным
интегралом называют не только множество
всех первообразных, но и любую функцию
этого множества.
37)Свойства неопределённого интеграла.
1.
; 
–производная
неопределенного интеграла равна
подынтегральной функции, а его
дифференциал–подынтегральному
выражению.
2.
–
неопределенный интеграл от дифференциала
некоторой функции равен этой функции
с точностью до постоянного слагаемого.
3.
–неопределенный
интеграл от алгебраической суммы
конечного числа функций равен
алгебраической сумме неопределенных
интегралов от этих функций.
4.
,
где k=const–постоянный
множитель можно вынести за знак
неопределенного интеграла.
38)Таблица интегралов.
1. |
|
11. |
|
2. |
|
12. |
|
3. |
|
13. |
|
4. |
|
14. |
|
5. |
|
15. |
|
6. |
|
16. |
|
7. |
|
17. |
|
8. |
|
18. |
|
9. |
|
19. |
|
10. |
|
20. |
|
39)Формулы замены переменной и интегрирования по частям.
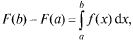Формула
замены переменной.
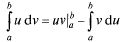Интегрирование
по частям.
40,41,42,43,44,45)Есть в тетради в лекции «интегрирование функций содержащих выражение ax^2+bx+c.
46)Интегрирование иррациональных Функций.
Для
интегрирования иррациональной функции,
содержащей 
используется
подстановка 
.
Чтобы
проинтегрировать иррациональную
функцию, содержащую несколько рациональных
степеней x,
применяется подстановка в форме
,
где n полагается
равным наименьшему общему кратному
знаменателей всех дробных степеней,
входящих в данную функцию.
Рациональная
функция x под
знаком корня n-ой
степени, т.е. выражение вида 
,
интегрируется с помощью подстановки 
.
47)Интегрирование Тригонометрических Функций.
1°. Интегралы вида
находятся с помощью тригонометрических формул
2°. Интегралы вида
где m и n - четные числа находятся с помощью формул понижения степени
Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)
3°. Если m = -m, n = -l - целые отрицательные числа одинаковой четности, то
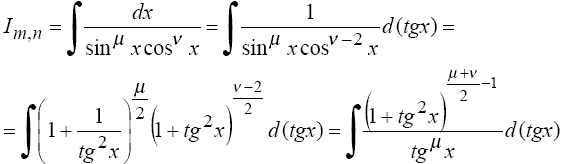
В частности, к этому случаю сводятся интегралы
4°. Интегралы вида
где
R - рациональная функция от sinx и cosx,
приводятся к интегралам от рациональных
функций новой переменной с помощью
подстановки
при
этом
Если
R{-sin x, cosx) = R(sinx, cosx), то целесообразно
применить подстановку tgx = t. при этом
