
- •Модуль числа
- •Предел чп. Теоремы о пределах.
- •Понятие функции. Предел функции в точке.
- •9,11)Непрерывность функции в точке, интервале и отрезке и их св-ва.
- •10)Точки разрыва и их классификация.
- •12)Понятие производной.
- •15)Правила дифференцирования.
- •16)Производные сложных функций.
- •17)Таблица производных.
- •18)Производные сложных функций
- •19)Дифференцирование функций заданных неясно.
- •24)Теорема Ферма.
- •25)Теорема Ролля.
- •26)Теорема Лагранжа.
- •27)Теорема Коши.
- •28)Правило Лопиталя.
- •29)Формулы Тейлора и Маклорена.
- •30)Разложение функций в ряд Маклорена.
- •31)Возрастание и убывание функции.
- •32)Экстремумы Функции.
- •33,34)Точки перегиба.
- •Вертикальная
- •Горизонтальная
- •Наклонная
- •35)Схема исследования функции.
- •36)Понятие первообразной и неопределённого интеграла.
- •37)Свойства неопределённого интеграла.
- •38)Таблица интегралов.
- •39)Формулы замены переменной и интегрирования по частям.
- •46)Интегрирование иррациональных Функций.
- •47)Интегрирование Тригонометрических Функций.
- •48,49)Определённый интеграл.
- •50)Интеграл с переменным верхним пределом.
- •60)Предел и непрерывность фнп.
- •62)Производная сложной фнп.
- •Связь с градиентом
- •65)Понятие экстремума фнп. Необходимое условие экстремума фнп.
- •67)Понятие числового ряда и его сходимости.
- •68)Необходимое условие сходимости числового ряда.
- •70)Признаки сходимости знакоположительных числовых рядов.
- •71)Абсолютная и условная сходимость знакопеременных числовых рядов.
- •72)Степенные ряды. Радиус и интервал сходимости степенного ряда.
- •74)Дифференциальные уравнения первого порядка.
- •75)Уравнения с разделяющимися переменными и их решение.
- •76)Задача Коши для дифференциального уравнения первого порядка.
24)Теорема Ферма.
Теорема утверждает, что:
Для любого натурального числа n > 2уравнение
|
25)Теорема Ролля.
Теорема Ро́лля (теорема о нуле производной) утверждает, что Если функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.
26)Теорема Лагранжа.
Формула
конечных приращений или теорема
Лагра́нжа о среднем значении утверждает,
что если функция f непрерывна на
отрезке[a;b] и дифференцируема в
интервале (a;b),
то найдётся такая точка ![]() ,
что
,
что
![]() .
.
Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Механическое
истолкование:
Пусть f(t) —
расстояние точки в момент t от
начального положения. Тогда f(b)
− f(a) есть
путь, пройденный с момента t = a до
момента t = b,
отношение ![]() —
средняя скорость за
этот промежуток.
—
средняя скорость за
этот промежуток.
27)Теорема Коши.
Пусть функции f(x) и g(x)
непрерывны на отрезке [a, b];
дифференцируемы в интервале (a, b);
"x О (a, b) g'(x) ≠ 0 .f '(c)
g '(c)
f = (b) − f(a) |
g(b) − g(a) |
|
|
28)Правило Лопиталя.
Правило
Лопита́ля —
метод нахождения пределов
функций, раскрывающий
неопределённости вида 0
/ 0 и ![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен
пределу отношения их производных.
Условия:
 или
или  ;
; и
и  дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности 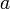 ;
; в
проколотой окрестности
;
в
проколотой окрестности
;существует
 ,
,
тогда
существует ![]() .
.
Пределы также могут быть односторонними.
29)Формулы Тейлора и Маклорена.
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:

где Rn − остаточный член в форме Лагранжа определяется выражением

Если
приведенное разложение сходится в
некотором интервале x,
т.е. ![]() ,
то оно называется рядом
Тейлора,
представляющим разложение функции f (x) в
точке a.
Если a
= 0,
то такое разложение называется рядом
Маклорена:
,
то оно называется рядом
Тейлора,
представляющим разложение функции f (x) в
точке a.
Если a
= 0,
то такое разложение называется рядом
Маклорена:

30)Разложение функций в ряд Маклорена.
|
|
31)Возрастание и убывание функции.
Определение 1. Функция f(x) называется возрастающей в интервале (a,b), если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если
f(x2) > f(x1) при x2 > x1.
|
|
Определение 2. Функция f (x) называется убывающей в интервале ( a, b ) если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если
f(x2) < f(x1) при x2 > x1.
Из этого определения следует, что у убывающей в интервале ( a, b ) функции f (x) в любой точке этого интервала приращения Dx и Dy имеют разные знаки.





