16)Производные сложных функций.

Пусть     - функция, дифференцируемая в точке   ,    - функция, дифференцируемая в точке    , причем   . Тогда    - сложная функция независимого переменного  , дифференцируема в точке     и ее производная в этой точке вычисляется по формуле    .

Обычно     называют внешней функцией, а  - внутренней. При вычислении производной сложной функции сначала дифференцируют внешнюю функцию, не обращая внимания на внутреннюю (ведь она может быть любой), затем умножают на производную конкретной внутренней функции.

17)Таблица производных.

18)Производные сложных функций

Пусть функция  дифференцируема и строго монотонна на  . Пусть также в точке  производная  . Тогда в точке    определена дифференцируемая функция  , которую называют обратной к   , а ее производная вычисляется по формуле  .

19)Дифференцирование функций заданных неясно.

Пусть функция F(x,y) удовлетворяет условиям

1. F(x₀,y₀) = 0 ;

2. частные производные F'_x и F'_y непрерывны в некоторой окрестности точки (x₀,y₀) ;

3. F'_y(x₀,y₀) ≠ 0 .

Тогда

1. уравнение F(x,y) = 0 определяет неявно в некоторой окрестности точки x₀ единственную непрерывную функцию y(x) , удовлетворяющую условию y(x₀) = y₀ .

2. функция y(x) имеет производную, непрерывную в окрестности точки x₀ .

Выясним смысл условий теоремы.

Существование непрерывной неявной функции y = f(x) в окрестности точки (x₀, y₀) следует из теоремы существования, так как:

• условие 1 гарантирует существование точки, координаты которой удовлетворяют уравнению F(x,y) = 0 ;

• из условия 2 следует непрерывность функции F(x,y) в окрестности точки (x₀,y₀) , а из условия 3 — ее монотонность по y при каждом фиксированном x из этой окрестности.

Следовательно, условия 1–3 обеспечивают выполнение условий существования неявной функции y(x) , удовлетворяющей условию y(x₀) = y₀ и непрерывной в окрестности точки x₀ .

20)Логарифмическая производная.

Логарифмическая производная — производная от натурального логарифма функции.

Логарифмическую производную используют, например, при дифференцировании (нахождении производной или дифференциала) степенно-показательной функции.

21)Функции заданные параметрически и их производная.

До сих пор функция записывалась в явном виде y= f(x) и в неявном F(x,y)=0. Но существует еще третий вид аналитического представления функции - это представление её в па раметрической форме в виде двух уравнений

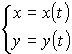
где t - вспомогательная переменная, называемая параметром.

22)Дифференциал функции.

Дифференциалом функции   в точке  называется линейная по   часть  приращения  . Дифференциал обозначается    , то есть  . Рассматривая функцию  , нетрудно убедиться, что   , если   - независимая переменная.

23)Производная и дифференциалы высших порядков.

Рассмотрим функцию   , определенную на некотором промежутке    . Вычислим производную  , которая также является функцией на  . Производной второго порядка от функции   называется производная от ее производной:    . Аналогично определяют производную любого порядка:   .

Рассмотрим дифференциал функции   в произвольной точке промежутка  :  . Здесь   - приращение независимой переменной, которое является числом и не зависит от  . Сам же дифференциал есть функция от  , и можно вычислить дифференциал от этой функции:    При   этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле  Аналогично вычисляется дифференциал любого порядка  .