9,11)Непрерывность функции в точке, интервале и отрезке и их св-ва.

Рассмотрим функцию  , определенную на некотором промежутке  . Функция   непрерывна в точке  , если предел функции в точке  равен значению функции в этой точке, .

Свойства: Функция, непрерывная в каждой точке промежутка  , называется непрерывной на промежутке. Для функции, непрерывной на отрезке  , справедливы следующие утверждения.

Функция, непрерывная на отрезке   , достигает на нем своих наибольшего и наименьшего значений, т.е. на отрезке   существуют точки   такие, что

.

Если функция   непрерывна на отрезке   и принимает на концах значения разных знаков, то на интервале   существует точка    , в которой функция обращается в нуль, т.е.    . Это утверждение применяют для отделения корней уравнений   с непрерывной левой частью — если найден отрезок, на концах которого функция принимает значения разных знаков, то можно утверждать, что на этом отрезке есть хотя бы один корень уравнения.

Если функция    непрерывна на отрезке     , дифференцируема хотя бы на интервале   , то на интервале   существует точка  , такая, что   . Это свойство называют формулой Лагранжа или формулой конечных приращений.

10)Точки разрыва и их классификация.

Если хотя бы одно из равенств   нарушается, говорят о разрыве в точке  . Если   и односторонние пределы конечны, то разрыв в точке  называется устранимым. Если  и оба односторонние пределы конечны, то говорят о скачке функции в точке  . Устранимый разрыв и скачок называются разрывами первого рода. Если один из односторонних пределов бесконечен или не существует, то разрыв называется разрывом второго рода. Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.

12)Понятие производной.

 Пусть функция   определена на промежутке  . Точка  — произвольная точка из области определения функции,    — приращение функции в точке  , вызванное приращением  независимой переменной    Производной функции  по независимой переменной   в точке  ,   называется предел отношения приращения функции  к приращению   при стремлении   к нулю, т.е.  

, 

— производная функции в точке  .

15)Правила дифференцирования.

Пусть функция   определена в некоторой окрестности точки   . Рассмотрим приращение функции в этой точке:   . Функция  называется дифференцируемой в точке , если ее приращение можно записать в виде  , где  - приращение независимой переменной, А – постоянная, не зависящая от  ,  - бесконечно малая функция при  .

Дифференциалом функции   в точке  называется линейная по   часть  приращения  . Дифференциал обозначается    , то есть  . Рассматривая функцию  , нетрудно убедиться, что   , если   - независимая переменная.

Воспользуемся определением производной для дифференцируемой функции  в точке  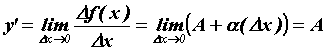:  . Таким образом, дифференциал функции выражается формулой   , то есть для вычисления дифференциала необходимо лишь вычислить производную и умножить ее на   . Поэтому часто слова “вычисление производной” и “дифференцирование” считают синонимами. Для того, чтобы функция была дифференцируема в точке, необходимо и достаточно, чтобы в этой точке существовала конечная производная.