1.1.2. Качество передачи сообщения.

Качество передачи аналогового сообщения (на­пример, разборчивость речи) оценивается эксперимен­тально, на основе чего определяются соответствующие нормы и стандарты.

Качество передачи дискретного сообщения оцени­вается коэффициентом частотности ошибок, т.е. отно­шением числа ошибочно принятых элементов к обще­му числу переданных элементов сообщения.

1.1.3. Спектральное представление электричес­кого сигнала.

Любой электрический сигнал можно разложить на некоторое число периодических сигналов, каждый из которых имеет постоянный период повторения его значения. Если рассматривается непрерывный периоди­ческий сигнал, то простейшим его видом является гар­моническое колебание (рис. 2, а).

Рис. 2. Разложение непериодического электрического сигнала на гармоники

Подбирая то или иное число гармоник с различным периодом их колебания, т.е. с различной их частотой, можно разложить на такие гармоники любой неперио­дический сигнал. Например, на рис. 2, б изображено разложение непрерывного непериодического сигнала (сплошная линия) на две гармоники с различными час­тотами (пунктирные линии). При более сложном виде передаваемого сигнала для его неискаженного представ­ления потребуется разложение сигнала на значительно большее число гармоник. Число гармоник, на которое разлагается сигнал, называют спектром частот этого сигнала. Для реальных сигналов, передаваемых по сети электросвязи, спектр частот для их неискаженной пере­дачи должен бы быть бесконечно широким. Однако на практике принимают ограниченный спектр частот, при котором существует пусть неидеальное, но достаточно приемлемое качество передачи, не приводящее к су­щественному искажению сигнала, а, следовательно, и сообщения.

Переменный ток

видимые лучи

радиоволны инфра- ультра-

красные фиолетовые рентгеновские

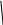
10 10² 10⁴ 10⁶ 10⁸ 10¹⁰ 10¹² 10¹⁴ 10¹⁶ 10¹⁸ 10²⁰

Частота, Гц

Рис. 3. Представление шкалы частот и волн для различных видов связи [34].

1.1.4 Представление непрерывных сигналов дискретными

_{Теорема Котельникова.}

Существует такой максимальный интервал времени между отсчетами: t, при котором имеется возможность безошибочного восстановления дискретизированной функции x(t), если спектр ее ограничен некоторой частотой _max.

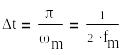
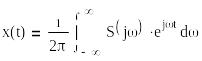
_{так как S(j)0 при -m<=<=m}

S(j)=0 при |_m|>_m,

то

(*)

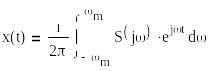
_{Поскольку ||<m, то можно записать ряд Фурье:}

(**)

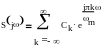
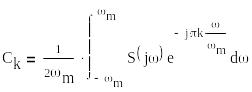
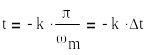
из (*) =>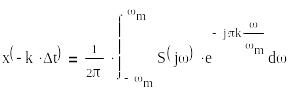

_{Сравнивая (*) и (**):}

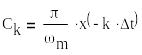
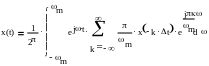
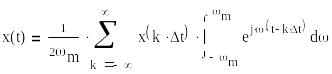
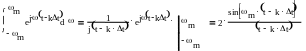
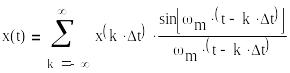
1.1.5 Аналоговые и цифровые сигналы

Пусть х(t) – аналоговый сигнал, а соответствующий ему цифровой сигнал (полученный в результате аналого-цифрового преобразования сигнала х(t) есть х(пТ), где Т – тактовый период, п – номер отсчета аналогового сигнала при его преобразовании в цифровую форму. пТ – тактовые моменты (моменты отсчета аналогового сигнала). При этом будем полагать, что аналоговый сигнал имеет ограниченный спектр и тактовый период удовлетворяет условию T<=1/(2Fmax).

В дальнейшем будем считать, что при t<0 х(t) = 0 и, следова­тельно, отличные от нуля значения x(пТ) могут иметь место лишь при пТ>=0 и п представляет собой последовательность (0, 1, 2, ...) чисел натурального ряда.

Известно, что операция получения спектральной функции Х (j) аналогового сигнала х (t) и обратная операция получения сигнала x(t) по известной его спектральной функции Х(j) производится с помощью пары преобразований Фурье:

(1.1)

(1.2)

Для цифрового сигнала спектральная функция последовательности x[пТ] обозначается Х(е^jωt), а преобразования Фурье определяются следующими выражениями:

(1.3)

(1.4)

Преобразование Фурье, независимо от того, проводится ли оно над аналоговым или дискретным сигналом, и независимо от того, явля­ется оно прямым или обратным, характеризуется следующим свойст­вом: преобразование Фурье, выполняемое над периодической функцией, приводит к дискретной функции, и, наоборот, преобразование Фурье дискретной функции является периодической функцией. Из этого сле­дует, что в случае, если аналоговая функция x(t) является дискретной, то ее спектральная функция является периодической. Если спектр Х(j) аналогового сигнала х(t) представляется функцией, изображен­ной на рис. 4 а), то после преобразования в цифровую форму сигнал будет описываться дискретной функцией х(пТ) и его спектральная функция будет периодической, как показано на рис. 4 б). Как видно из рис. 4 в пределах интервала -/T<=<=/T модуль спектраль­ной функции аналогового и цифрового сигналов подобны. При ограни­ченном спектре аналогового сигнала спектр цифрового сигнала оказы­вается неограниченным и имеет периодическую структуру с периодом 2Т. Отсюда следует прием, используемый для получения аналогового сигнала х(t) из цифрового сигнала х(пТ): достаточно цифровую после­довательность преобразовать в последовательность импульсов, име­ющих малую длительность, и амплитуды, равные х(пТ), а затем из спектра такого дискретного сигнала с помощью фильтра нижних частот выделить ту ее часть в интервале 0<=<=/Т, которая совпадает со спектром аналогового сигнала. При этом на выходе фильтра образует­ся аналоговый сигнал х(t), соответствующий цифровому сигналу х(пТ).

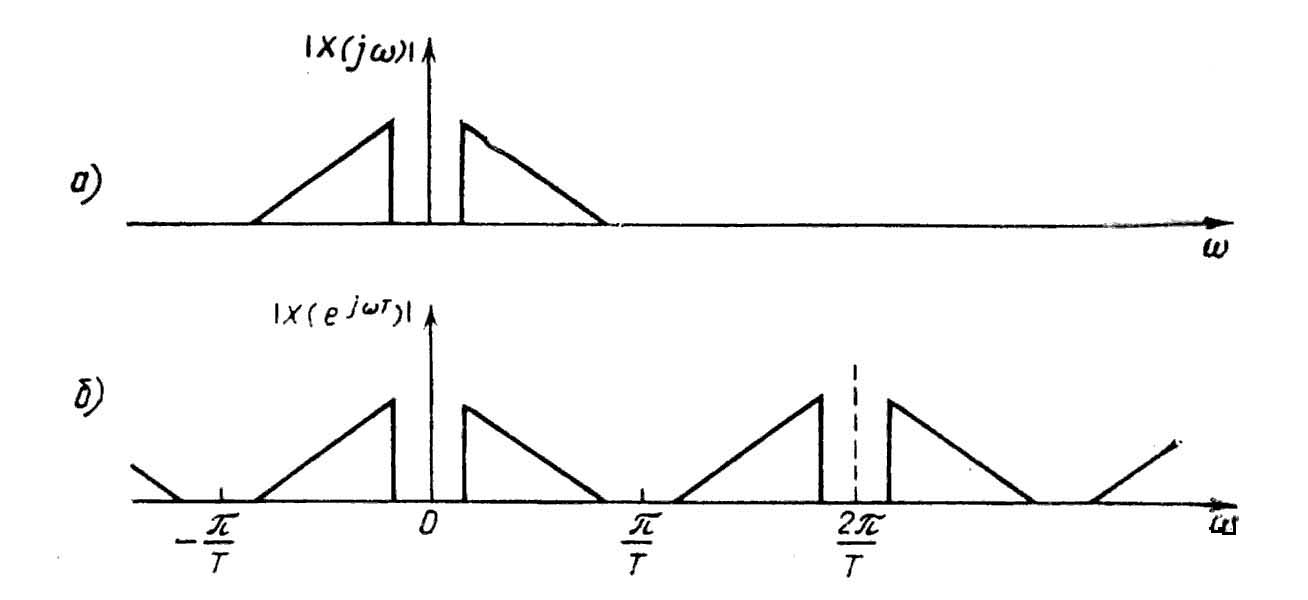
Рис. 4. Спектральные функции: а) непрерывного сигнала; б) дискретного сигнала.

Предположим, что берутся отсчеты непрерывного действи­тельнозначного сигнала x(t) с ограниченным спектром, верхняя частота которого равна F₀ герц, так что НВПФ сигнала x(t) равно нулю при |f|>F₀. НВПФ действительного сигнала x(t) —это всегда симметричная функция с полной шириной спектра, равной 2F₀, Гц; см. рис. 5, а. Отсчеты сигнала x(t) могут быть получены посредством умножения этого сигнала на функцию отсчетов:

x_s(t)=x(t)*TS= (1.5)

Напомним читателю, что приведенное в (1.5) произведение x(t) с последовательностью импульсных функций должно рас­сматриваться подобно выражению (2.4). В соответствии с теоре­мой свертки в частотной области, НВПФ сигнала х(t) – это просто свертка спектра сигнала x(t) и преобразования Фурье функции отсчетов по времени (TS):

X_s(f)=X(f)*F{TS}= (1.6)

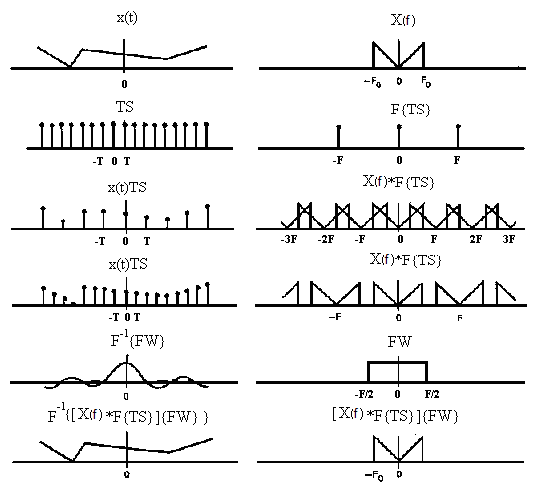
Рис. 5. Иллюстрация теоремы отсчетов во временной области для действи­тельного сигнала с ограниченным спектром: а — исходная функция времени с ограниченным спектром и ее преобразование Фурье; б— функция отсчетов по вре­мени и ее преобразование Фурье; в—временные отсчеты исходной функции и ее преобразование Фурье; в — временные отсчеты исходной функции и ее перио­дическое продолженное преобразование Фурье для случая F₀>1/2T; г— временные отсчеты исходной функции и ее периодически продолженное преобра­зование Фурье для случая F₀<1/2T; д—частотное окно (идеальный фильтр нижних частот) и его преобразование Фурье (функция sinc); e—исходная функция времени, восстановленная посредством операции свертки с функци­ей sinc.

Свертка X(f) с преобразованием Фурье функции отсчетов F{TS}=Ш_l/T(f) просто периодически продолжает X(f) с час­тотным интервалом 1/Т Гц, соответствующим частотному ин­тервалу между импульсными функциями. Поэтому Xs(f) пред­ставляет собой периодически продолженный спектр X(f). Имен­но по этой причине функцию Ш(f) часто называют функцией периодического продолжения. В общем случае отсчеты в одной области (например, временной) приводят к периодическому продолжению в области преобразования (например, частотной). Если частота отсчетов выбрана достаточно низкой, так что F<2F₀, то периодически продолженные спектры будут пе­рекрываться с соседними, как показано на рис. 5, в. Это пе­рекрытие – одна из форм искажения и носит название эффекта наложения в частотной области. Если частота отсчетов повы­шается так, что F>=2F₀, то перекрытие спектров будет отсут­ствовать, что показано на рис. 5, г. Частота отсчетов F_N=2Р₀ получила название частоты отсчетов Найквиста, или частоты сворачивания.

Для того чтобы восстановить исходный временной сигнал по его отсчетам, т.е. осуществить интерполяцию некоторого континуума значений между этими отсчетами, можно пропус­тить дискретизованные данные через идеальный фильтр нижних частот (ФНЧ), обладающий прямоугольной частотной характе­ристикой, показанной на рис. 5, д. В результате (см. рис. 5,е):

X(f) =X_s(f) • FW = [X (f) *F{TS}]FW (1.7)

восстанавливается исходное НВПФ. Используя теоремы о сверт­ке во временной и частотной областях, получаем:

х (t) = х_s(t) *F^-1 {FW} = [x (t) • TS] * F^-1 {FW} = (2.37)

Выражение (2.37) представляет собой математическую запись теоремы отсчетов во временной области, которая утверждает, что с помощью интерполяционной формулы (2.37) действитель­ный сигнал с ограниченным спектром может быть точно вос­становлен по бесконечному числу известных временных отсче­тов, взятых с частотой F>=2F₀. Аналогичный подход может быть использован и в случае комплексных сигналов с ограни­ченным спектром с шириной спектра, равной 2F₀ герц.

Дуальной к теореме (2.37) является теорема отсчетов в частотной области. Теперь вместо сигнала с ограниченным спектром рассмотрим действительный сигнал с ограниченной длительностью, т. е. некоторый сигнал x(t), который равен ну­лю при |t|>T₀. Если будем выполнять дискретизацию не во временной, а в частотной области с частотными интервалами F<=1/2T₀ (в противном случае будет возникать наложение во времени), то получим периодическое продолжение неперекры­вающихся сигналов с ограниченной длительностью. Применение идеального прямоугольного временного окна будет восстанавливать ограниченный по длительности исходный сигнал; в час­тотной области это будет соответствовать некоторой операции фильтрации, используемой для восстановления исходного пре­образования. Операции во временной области, характеризую­щие теорему отсчетов в частотной области, описываются выра­жением

x(t)=[x(t)*F^-1{FS}]TW, (1.8)

а операции получения соответствующих преобразований – вы­ражением:

X(f)=[X(f)FS]*F{TW}= Х(n/2T₀)sinc(2Tо[f-n/2T₀)])=

= X(nF)sinc([f-nF]/F), (1.9)

описывающим процедуру интерполяции ОД-сигнала, при кото­рой F<=1/2T₀. Таким образом, НВПФ X{f) некоторого сигнала с ограниченной длительностью может быть однозначно восста­новлено по равномерным (эквидистантным) отсчетам спектра такого сигнала, если выбранный интервал отсчетов по частоте удовлетворяет условию F<=1/2Т₀ герц.

.