8. Существование предела монотонной огран. Послед.

Определение 2.

Последовательность {x_n} называется возрастающей (строго возрастающей) если x_n+1 x_n (x_n+1 > x_n) для ∀n ∈ N. Последовательность {x_n} называется убывающей (строго убывающей) если x_n+1 x_n (x_n+1 < x_n) для ∀n ∈ N. Определение 3. Возрастающие и убывающие последо-вательности называются монотонными последователь-ностями. Теорема 5 (Вейерштрасс). Для того чтобы неубывающая последовательность имела предел, необходимо и доста-точно, чтобы она была ограниченной сверху. Доказательство. То, что любая сходящаяся последова-тельность ограничена, было доказано при рассмотрении общих свойств предела последовательности. Пусть {x_n} неубывающая последовательность ограниченная сверху. Тогда множество {x_n | n ∈ N} ограничено сверху.Согласно основной лемме это множество имеет верхнюю грань a = sup x_n. По определению верхней грани для любого ε > 0 найдется элемент x_N ∈ {x_n} такой, что a−ε < x_N a. Поскольку последовательность {x_n} неубывающая, то при любом n > N получаем a − ε < x_N x_n a, т.е. a − ε < x_n < a+ε или |x_n−a| < ε.

Поэтому _n=a.

9.Предел. Послед. И арифмет. Операц.

Определение 2. Число a называется пределом числовой последовательности {x_n}, если для любого сколь угодно малого положительного числа ε найдется такое натуральное число n₀ = n₀(ε), что для всех выполняется

Неравенство В этом случае говорят, что последовательность имеет предел и пишут

м ожно записать более кратко:

Последовательности, имеющие предел называют сходящимися (к числу a), а последовательности, не имеющие конечного предела - расходящимися.Понятие предела последовательности связано в определенном смысле с встречающейся на практике задачей получения значения некоторой интересующей нас величины с наперед заданной фиксированной точностью ε > 0. Последовательные приближенные значения x_n, рассматриваемой величины могут получаться в результате проведения каких-либо экспериментов, или вычисления по каким-нибудь рекуррентным формулам или каким-то другим путем. Эта задача будет, очевидно, решена, если найдется номер n₀, начиная с которого все значения x_n будут отклоняться от точного значения a рассматриваемой величины в пределах заданной точности. Конечно, если указанное n₀ существует лишь для одного данного ε > 0, это еще не означает, что последовательность {x_n} сходится: в определении предела последовательности требуется, чтобы соответствующий номер n₀ можно было бы подобрать для любого ε > 0. Так как {|x_n − a| < ε} = V (a, ε), то из определения предела следует, что если число a является пределом последовательности {x_n}, то в произвольную сколь угодно малую ε-окрестность точки попадают все члены этой последовательности, начиная с некоторого n > n₀ ∈ N. Арифмет. Операц. Определение 3. Если {x_n}, {y_n} - две числовые последовательности,то их суммой,произведением и частным называются соответственно последовательности {x_n + y_n}, {x_ny_n}, {x_n/y_n} (при делении предполагается, что все члены последовательности {y_n} отличны то нуля). Теорема 2. 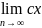Если последовательности {x_n}, {y_n} сходятся и _n=a и _n=b то, а) _n y_n= _{n n} =a б) _n =c _n =c*a, c \{0} в) _n y_n = _{n n} =a*b г) = _n \ _n=a\b

Доказательство. Докажем случай г). Имеем. _n=a

⇔ ∀ε > 0 ∃N₁ ∈ N : ∀n > N₁ ⇒ |x_n − a| < ε и _n=b ⇔ ∀ε > 0 ∃N₂ ∈ N : ∀n > N₂ ⇒ |y_n − b| < ε . Поскольку b 0, то ∃δ > 0 ∃N₃ ∈ N : ∀n > N₃ ⇒ |y_n| > δ > 0. Пусть N = max{N₁,N₂,N₃}. Тогда имеем