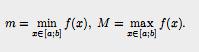55.Критерий Коши интегрируемости функций.

Теорема 2. Для того, чтобы функция f(x) была интегрируема на отрезке [a; b], необходимо и достаточно, чтобы для любого ε > 0 существовало такое δ > 0, что, каковы ни были разбиения τ’= {x’_i}i=n’ i=0 и τ’’= {x’’_i }i=n’’ i=0 диаметра

меньше δ, т.е. |τ’| < δ, |τ’’| < δ и точки ξ’_i ∈ [x’_i−1; x’_i], i = 1, n’, ξ’’_j ∈ [x’’_j−1; x’’_j ], j = 1, n’’, выполнялось неравенство

Доказательство. Если функция f(x) интегрируема, то существует предел (1.1), то есть для любого ε > 0 существует

такое δ > 0, что для любого разбиения τ = {x_i}i=n i=0 диаметра меньше δ, т.е. |τ | < δ, и при любом выборе точек

ξ_i ∈ [x_i−1; x_i], i = 1, n для интегрируемых сумм σ_τ выполняется неравенство

Если теперь σ’ и σ’’ две такие интегральные суммы, что |τ ‘| < δ, |τ’’| < δ, то

Достаточное условие интегрируемости функции. Пусть Число ω(f,E) называется колебанием функции f(x) на E. Если τ = {x_i}i=n i=0 разбиения отрезка [a; b], E_i = [x_i−1; x_i], то называется интегральным колебанием функции f(x) на [a; b].

Теорема 3 (достаточное условие интегрируемости). Чтобы ограниченная функция f(x) на [a; b] была интегрируемой на [a; b] достаточно, чтобы для любого ε > 0 существовало δ > 0, что для любого разбиения τ = {x_i}i=n i=0 диаметра |τ | < δ выполнялось условие

56. Критерий Дарбу интегрир. Ф-ций. Теорема 9 (Критерий Дарбу). Для того, чтобы ограниченная на отрезке функция была на нем интегрируема по

Риману, необходимо и достаточно, чтобы были равны ее верхний и нижний интегралы Дарбу.

Доказательство.

Необходимость. Пусть функция f(x) интегрируема на [a; b]. Так как s_τ <= I_∗ <= I^∗ <= S_τ , то 0 <= I^∗ − I_∗ <= S_τ − s_τ , и

так как для интегрируемой функции

то I^∗ = I_∗

Достаточность. Если f(x) ограничена на отрезке [a; b] функция и I^∗ = I_∗, то, в силу теорем 7 и8

что и означает интегрируемость функции f(x) на отрезке [a; b].

57.Классы интегрируемых функций.

Теорема 4. Если функция f(x) непрерывна на отрезке [a; b], то она интегрируема по Риману на этом отрезке.

Доказательство. Очевидно, что если τ = {x_i}i=ni=0 - разбиение отрезка [a; b] диаметра |τ | < δ, то f(x) непрерывна на

частичных отрезках E_k. Согласно теореме Кантора она равномерно непрерывна на каждом E_k. Это означает

Тогда

т.е. выполнено достаточное условие интегрируемости. Теорема 5. Если функция f(x) непрерывна на отрезке [a; b] за исключением конечного числа точек и ограничена на нем, то f(x) интегрируема на [a; b].Доказательство. Так как f(x) ограничена на [a; b], то существует A > 0, что

Тогда ω(f,E) < A, где E = [a; b]. Пусть функция f(x) имеет ` точек разрыва c<sub>1</sub>, c<sub>2</sub>, . . . , c`. Пусть ε > 0 – произвольное фиксированное число. Возьмем δ₁ = ε/8Al . Построим окрестности V_δ1 (ci), i = 1, l точек c_i. Обозначим Возьмем произвольное разбиение τ ={x_i}i=n i=0 отрезка E диаметра |τ | < δ < δ1.Запишем соответствующие интегральные колебания

которые представим в виде двух сумм

где Σ₁ относится к тем отрезкам разбиения, которые не имеют с U общих точек, Σ₂ соответствует остальным отрезкам из E.Тогда для слагаемых Σ₁ можно дать следующую оценку (смотри доказательство теоремы 4)

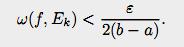
Поэтому

Оценим Σ₂. Прежде всего заметим, что для слагаемых Σ₂ имеем ω(f,Ek) < A. Сумма длин частичных отрезков не

превосходит числа

В итоге

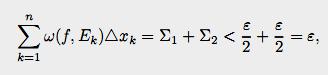т.е. выполнено достаточное условие интегрируемости. Теорема 6. Если функция f(x) монотонна на отрезке [a; b], то она интегрируема на [a; b].

5 9. Теорема о среднем для интеграла. Теорема 15 (Первая теорема о среднем для интеграла). Пусть f, g ∈ R[a; b], m =

Если функция g(x) неотрицательна (или не положительна) на отрезке [a; b], то

(1)

г де µ ∈ [m;M]. Если, кроме того, известно, что f ∈ C[a; b], то найдется ξ ∈ [a; b] такая, что

(2)

Доказательство. Поскольку перестановка пределов интегрирования приводит к изменению знака одновременно в обеих частях равенства (1), то достаточно проверить это равенство в случае a < b. Изменение знака функции g(x) тоже одновременно меняет знак обеих частей равенства (1), поэтому без ограничения общности доказательства будем считать, что g(x) 0 на [a; b].

Поскольку то при g(x) 0 имеем

Поскольку m · g ∈ R[a; b], f · g ∈ R[a; b], M · g ∈ R[a; b], то, применяя теорему13, получим

Е сли то, как видно из этих неравенств,

с оотношение (1) выполнено. Если же

то полагая

находим, что µ ∈ [m;M], но это равносильно соотношению (1). Равенство (2) следует из (1) из теоремы о промежуточном значении для функции f ∈ C[a; b], с учетом того, что в случае f ∈ C[a; b]