48.Интегрирование подстановкой .

Теорема 2. Пусть определенные соответственно на числовых промежутках Jx и Jt функции f : Jx → R и ϕ : Jt → R

обладают следующими свойствами:1) значение ϕ(t) ∈ Jx, ∀t ∈ Jt; 2) на числовом промежутке Jx функция f(x) имеет первообразную F : Jx → R, то есть

3) функция ϕ дифференцируема на Jt.

Тогда на числовом промежутке Jt сложная функция F(ϕ(t))

, ∀t ∈ Jt является первообразной функции f(ϕ(t))ϕ’(t), ∀t ∈ Jt и

Доказательство. То, что при любом t ∈ Jt значение ϕ(t) ∈ Jx, позволяет говорить о существовании сложных функций f(ϕ(t))и F(ϕ(t))на Jt. Из соотношения (2.2) следует,что F’(x) = f(x), ∀x ∈ Jx. Тогда по правилу дифференцирования

сложной функции

Это означает, что на Jt функция f(ϕ(t))· ϕ’(t) имеет первообразную Fϕ(t). Отсюда, согласно определению

неопределенного интеграла, следует, что

Поскольку

Пример 3. Найти

Решение. Сделаем подстановку e^x − 1 = t². Тогда x = ln(t² + 1) и dx = . Подставляя

49.Интегрирование по частям.

Теорема 3. Если функции u(x) и v(x) дифференцируемы на некотором промежутке X и на этом промежутке

существует интеграл vdu, то на нем существует и интеграл udv, причем

Доказательство. Пусть функции u(x) и v(x)дифференцируемы на промежутке X. Тогда по правилу дифференцирования произведения для всех точек этого промежутка имеет место равенство d(uv) = vdu + udv и поэтому udv = d(uv) – vdu

Интеграл от каждого слагаемого правой части существует, так как, согласно свойству 2⁰

^{а интеграл vdu существует по условию. Поэтому на основании свойства 4 существует и интеграл udv, причем}

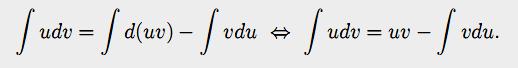
^{Соотношение (2.5) называется формулой интегрирования по частям. С помощью этой формулы отыскание интеграла}

^{udv можно свести к вычислению другого интегралаvdu. Применять ее целесообразно, когда интеграл в правой части}

^{формулы (2.5) более прост для вычисления, чем исходный.}

50.Интегрирование рациональных функций.

Р ассмотрим функцию f(x) = P(x)/Q(x), где P(x), Q(x) - многочлены с действительными коэффициентами.Рациональная дробь P(x)/Q(x) называется правильной, если либо P(x) - нулевой многочлен, либо его степень меньше степени многочлена Q(x), и неправильной, если степень многочлена P(x) не меньше степени многочлена Q(x).Если рациональная дробь P(x)/Q(x)неправильная, то, разделив числитель на знаменатель по правилу деления многочленов, получим равенство

где R(x), P1(x), Q1(x) - некоторые многочлены, а P1(x)/ Q1(x)- правильная рациональная дробь. Лемма 1. Пусть P(x)/Q(x)- правильная рациональная дробь. Если число a является действительным корнем кратностиα >= 1 многочлена Q(x), т.е.

т о существуют действительное число A и многочлен P1(x) с действительными коэффициентами такие, что

где дробь P1(x)/(x−α)^α−1Q₁(x)также является правильной.

Лемма 2. Пусть P(x)/ Q(x)- правильная рациональная дробь. Если

то существуют действительные числа M, N и многочлен P₁(x) с действительными коэффициентами такие, что

где дробь P1(x)/ (x²+px+q)^β−1Q₁(x) также является правильной. Теорема 4. Пусть P(x)/Q(x)- правильная рациональная дробь, P(x), Q(x) - многочлены с действительными коэффициентами. Если

где a_i - попарно различные действительные корни многочлена Q(x) кратности α_i, i = 1, r, p2_j − 4q_j < 0, j = 1, s, то

существуют действительные числа A_i^(α)i , i = 1, r, α = 1, α_i, M_j^(β)

, N_j^(β), j = 1, s, β = 1, β_j , такие, что

Рациональные дроби вида A/(x−a)^α A ≠0 и Mx+N/(x²+px+q)^β M² + N² ≠0, где a, p, q, A, M и N - действительные числа и ((p2/4)-q) < 0 (корни квадратного трехчлена x²+px+q комплексные), называются элементарными рациональными дробями.Таким образом, теорема утверждает, что всякая ненулевая правильная рациональная дробь может быть разложенана сумму элементарных рациональных дробей.

Чтобы найти коэффициенты разложения, чаще всего применяют метод неопределенных коэффициентов и метод

частных значений.