36. Теорема Ферма.

Определение 1. Точка x₀ ∈ X называется точкой локального максимума (минимума) функции f(x), а значение в ней локальным максимумом (минимумом), если существует окрестность V (x₀ ) точки x₀ , такая, что ∀x ∈ V (x₀ ) имеем f(x)≤f(x₀) (f(x)≥f(x₀)).

Определение 2. Точка x₀∈ X называется точкой строгого локального максимума (минимума) функции f(x), если существует проколотая окрестность 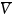(x₀) точки x₀, такая, что ∀x ∈ (x₀) имеем f(x) < f(x₀) (f(x)>f(x₀)).

Определение 3. Точки локального максимума и минимума называются точками локального экстремума, а значения функции в них - локальными экстремумами функции.

Заметим, что если x₀ точка строгого локального экстремума функции f(x), то приращение ∆f(x₀ ) = f(x₀ + ∆x) − f(x₀), ∀x ∈ (x₀) сохраняет знак.

Теорема 6 (Ферма). Пусть функция f(x) определена на интервале (a;b) и в некоторой точке x₀ ∈ (a; b) имеет локальный экстремум. Тогда, если в точке x₀ существует конечная производная f’(x₀) , то f’(x₀) = 0.

Доказательство. Пусть для определенности в точке x₀ функция имеет локальный минимум, т.е. f(x)≥ f(x₀), ∀x ∈ V (x₀). Тогда в силу дифференцируемости функции f(x) в точке x₀ при x > x₀ получим

а при x < x₀ будем иметь

Эти неравенства имеют место одновременно лишь при f’₊(x₀)=f’_-(x₀)=f’(x₀)=0.

Замечание 1. Геометрический смысл теоремы Ферма состоит в следующем: если точка x₀ ∈ (a; b) является точкой максимума или минимума функции и существует f’(x₀), то касательная, проведенная к графику функции в точке (x₀,f(x₀))параллельна оси Ox.

Замечание 2. Оба условия – интервал (a;b) и дифференцируемость функции в точке локального экстремума – обяза- тельны для справедливости теоремы Ферма. Действительно, пусть f(x) = |x|, x ∈ (−1;1). В точке x₀= 0 функция f(x) имеет локальный минимум, но в ней она не дифференцируема. В данном случае условие существования производной в точке локального минимума нарушено и поэтому теорема Ферма не имеет места.

Пусть теперь f(x) = x³, x ∈ [−1;1]. В точке x₀ = 1 имеется краевой максимум, но f’(1)=3≠0. Теорема Ферма не применима в данном случае, поскольку x = 1 (−1;1).

37. Теорема Ролля.

Теорема 7. Пусть функция f(x) непрерывна на отрезке [a;b], дифференцируема в каждой точке интервала (a; b) и f(a) = f(b). Тогда существует хотя бы одна точка ξ, a < ξ < b, такая, что f’(ξ) = 0.

Доказательство. Если f(x) – постоянная на [a; b], то f’(x) = 0, ∀x ∈ (a; b).

Пусть теперь f(x) не является постоянной функцией. Непрерывная на отрезке [a;b] функция по теореме Вейерштрасса достигает в некоторых точках отрезка [a; b] наибольшего и наименьшего значений. Поскольку f(x) не является постоянной, то или или обязательно достигаются функцией во внутренней точке ξ отрезка [a; b].

По теореме Ферма f’(ξ) = 0.

Замечание 3. Геометрический смысл теоремы Ролля следующий: при выполнении условий теоремы внутри отрезка [a;b] обязательно найдется хотя бы одна точка ξ, такая, что касательная к графику f(x) в точке (ξ,f(ξ)) параллельна оси Ox.

Следствие 1 (Обобщенная теорема Ролля). Пусть функция f(x) n раз непрерывно дифференцируема на отрезке [a; b] и обращается в нуль в n + 1-й точке x₀ , x₁ , x₂ , ... ,x_n этого отрезка. Тогда существует такое число ξ ∈ (a;b), что f⁽ⁿ⁾(ξ) = 0.

Доказательство. Для простотырассуждений ограничимся случаем n = 2, т.е. функция f(x) обращаетсяв нуль в точках x₀ , x₁ , x₂ . Для определенности будем считать, что x₀ < x₁ < x₂ . Так как f(x₀) = f(x₁) = f(x₂) = 0, то по теореме Ролля существует ξ₁ ∈ (x₀; x₁), что f’ (ξ₁) = 0, и существует, ξ₂∈(x₁;x₂), что f’(ξ₂)=0. Итак, на концах отрезка [ξ₁;ξ₂] выполнено условие f’(ξ₁ )=f’(ξ₂) = 0. По теореме Ролля на отрезке [ξ₁ ;ξ₂] существует точка ξ в которой f’’(ξ) = 0.