1 2.3. Непрерывность функции в точке. Действия над непрерыв функциями

x=x₀+x, x=x-x₀

y=f(x₀+x)-f(x₀)

Ф-ция y=f(x) наз. непрерывной в точке x₀, если она определена в окрестности этой точки, а limy=0. (бесконеч.малая. приращению аргумента соответствует б.м. приращению ф-ции).

limy=lim[f(x)-f(x₀)]=limf(x)-limf(x₀)=0, то

limf(x)=limf(x₀)

xx₀

Ф-ция непрерывна в точке х₀, если ее предел = значению этой ф-ции в точке х₀

Ф-ция явл. непрерывной на интервале, если она непрерывна в каждой его точке.

13. Классификация точек разрыва.

Если хотя бы одно из равенств нарушается, говорят о разрыве в точке . Если  и односторонние пределы конечны, то разрыв в точке называется устранимым. Если и оба односторонние пределы конечны, то говорят о скачке функции в точке . Устранимый разрыв и скачок называются разрывами первого рода. Если один из односторонних пределов бесконечен или не существует, то разрыв называется разрывом второго рода. Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.

5.3 Свойства бесконечно малых функций:

1.Сумма фиксированного числа бесконечно малых функций при ха тоже бесконечно малая функция при ха.

2.Произведение фиксированного числа бесконечно малых функций при ха тоже бесконечно малая функция при ха.

3.Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при ха.

4.Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

4.4 Бесконечно большие и бесконечно малые функции. Связь между ними

О пределение. Предел функции f(x) при ха, где а- число, равен бесконечности, если для любого числа М>0 существует такое число >0, что неравенствоf(x)>M выполняется при всех х, удовлетворяющих условию 0 < x - a <  Записывается 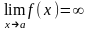. Собственно, если в приведенном выше определении заменить условие f(x)>M на f(x)>M, то получим: а если заменить на f(x)<M, то: 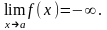Графически приведенные выше случаи можно проиллюстрировать следующим образом:

Определение. Функция называется бесконечно большой при ха, где а – чосли или одна из величин , + или -, если , где А – число или одна из величин , + или -. Функция f(x) называется бесконечно малой при ха, где а может быть числом или одной из величин , + или -, если

Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.Теорема. Если f(x)0 при ха (если х ) и не обращается в ноль, то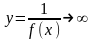

2. Теорема об ограниченности сходящеся последовательности. Теоре Вейерштрасса.

Теорем (1 теорема Вейерштрасса)

Если фун-я непрерывна на сегменте, то она ограничена на нем.

Дока-ство: методом от противного, воспользуемся свойством замкнутости сегмента [a,b]. Из любой последовательности (x_n) этого сегмента можем выделить подпоследовательность , сходящуюся к .

Пусть f не ограничена на сегменте [a;b], например, сверху, тогда для всякого натурального  найдется точка , что . Придавая n значения 1,2,3,…, мы получим последовательность (x_n) точек сегмента [a;b] для которых выполнено свойство f(x₁)>1,f(x₂)>2,f(x₃)>3,…,f(x_n)>n…

Последовательность  ограничена и поэтому из нее по теореме можно выделить подпоследовательность _{> >}, которая сходится к точке :  (1)

Рассмотрим соответствующую последовательность . С одной стороны   и поэтому   (2),

С другой стороны, учитывая определение непрерывной функции по Гейне из (1) будем иметь      (3)

Получаем равенства (2) и (3) противоречат теореме (о единственности предела). Это противоречие и доказывает справедливость Т. Аналогично доказывается ограниченность функции снизу. Ч.Т.Д.