3. Обмен между выигрышем от ортогонального кодирования и шириной полосы.

Оценим теперь выигрыш, который сопровождает применение ортогональных сигналов со случаем отсутствия кодирования, т.е. непосредственной передачей потока информационных бит источника. Предположим, что энергетический ресурс позволяет передавать каждый бит данных с энергией , отсутствует специальное кодирование потока бит данных и каждый информационный бит передается оптимальным образом с помощью пары противоположных сигналов, другими словами используется БФМ. Среди блоков из последовательных бит возможны любые комбинации, в том числе и такие, которые отличаются друг от друга значением только одного бита. Поэтому минимальная величина квадрата расстояния между сигналами, отвечающими не идентичным –битовым блокам, совпадает со значением квадрата расстояния между однобитовыми противоположными сигналами, т.е. согласно рис. 2.4, а , где второй индекс обозначает отсутствие кодирования (uncoded).

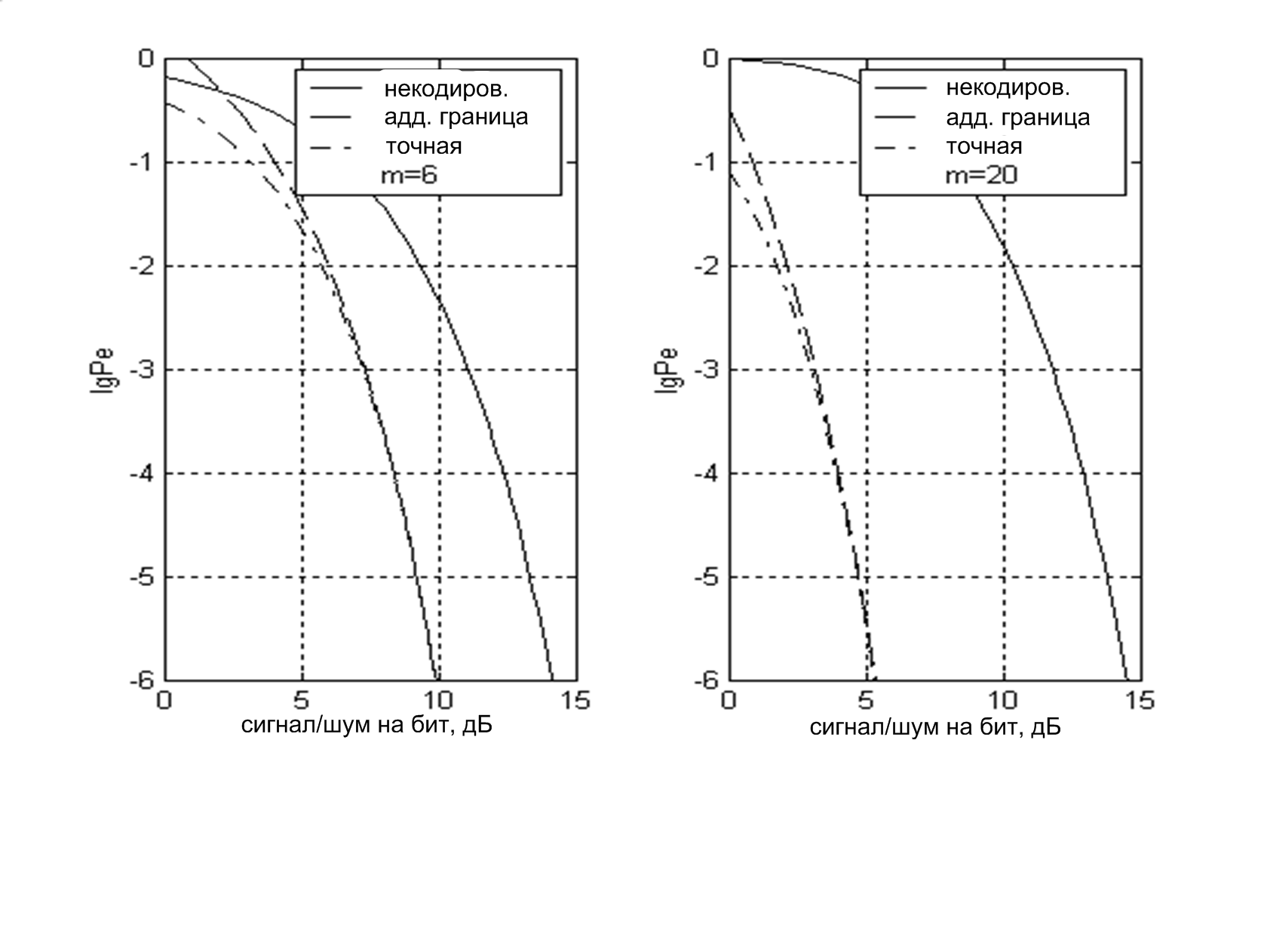
Рис. 2.21. Сравнение вероятности ошибки для некодированной передачи и ортогональной сигнализации

Рассмотрим теперь другую систему, в которой все различные –битовые блоки передаются ортогональными сигналами. Ясно, что каждый такой сигнал характеризуется энергией, равной , сохраняя неизменной ее значение на бит . Тогда квадрат расстояния (одинаковый для любой пары сигналов, поскольку ортогональные сигналы эквидистантны) между сигналами снова легко может быть определен на основании рис.2.4, b: . Очевидно, что выигрыш ортогональных сигналов в величине минимума квадрата расстояния у варианта отсутствия кодирования составляет . При альтернативном подходе для обеспечения одинакового минимума расстояния передача данных без кодирования требует энергетических затрат в больше, чем в случае ортогонального кодирования. Принимая во внимание соотношение (2.29), минимум расстояния асимптотически определяет вероятность ошибки для любых сигналов, используемых в –ичной передаче. Следовательно, требование высокой достоверности приема, автоматически влекущее за собой необходимость высокого значения отношения сигнал-шум, означает, что одинаковая надежность двух рассмотренных систем возможна только в случае раз больших энергетических затратах для варианта без кодирования. Таким образом, асимптотический выигрыш от кодирования ортогональными сигналами является адекватным показателем преимущества ортогональной сигнализации в пределе, т.е. при отношении сигнал-шум, стремящемся к бесконечности.

Для определения величины выигрыша от ортогонального кодирования при конечном значении отношения сигнал-шум, также как скорости его сходимости к асимптотическому случаю на рис.2.21 представлены семейства кривых для двух значений длины –битового блока: и . Первая кривая (сплошная линия) демонстрирует вероятность ошибочного приема некодированного блока, а две других вычислены в предположении кодирования –битовых блоков ортогональными сигналами, которые обрабатываются когерентно. Пунктирная кривая построена на основании аддитивной границы (2.37), тогда как кривая, обозначенная через точку и тире, отвечает точной формуле вычисления вероятности ошибки когерентного приема ортогональных сигналов, вывод которой можно найти во многих популярных книгах по основам теории связи [например 1,3]:

,

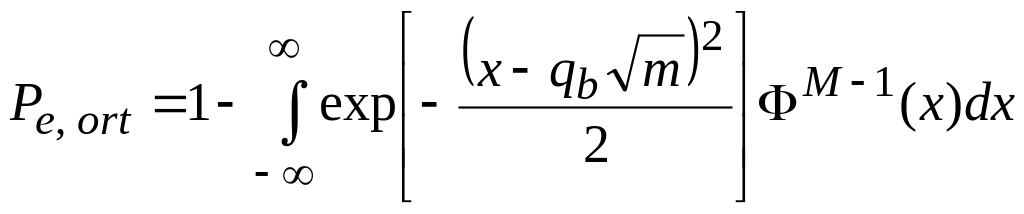где – отношение сигнал-шум на бит, а – функция ошибок.

Основной вывод, который следует из графиков на рис. 2.21, состоит в высокой достоверности аддитивной границы. В области типичных для практики требований к вероятности ошибки просвет между величиной отношения сигнал-шум на бит, оцененного из границы и вычисленного точно, составляет менее 0.5 дБ ( ) и быстро уменьшается с ростом требований к достоверности передачи (менее 0.2 дБ при ). В диапазоне значений от до действительный выигрыш от ортогонального кодирования возрастает с 3,5 до 4,2 дБ ( ) и от 8,5 до 8,9 дБ ( ). Сравнивая эти цифры с асимптотическими значениями (4.8 и 10 дБ соответственно), нетрудно увидеть более чем хорошее совпадение между ними, оправдывающее использование асимптотического выигрыша от кодирования в качестве первого приближения оценки эффективности ортогонального кодирования.

Очень оптимистическое мнение об ортогональной сигнализации, которое может возникнуть свете приведенных выше результатов, значительно снижается реальной стоимостью выигрыша от кодирования. Последний приобретается за счет расширения полосы, поскольку, как это было установлено в 2.3, размерность сигнально пространства , т.е. число ортогональных сигналов , непосредственно определяется общим частотно-временным ресурсом системы. Интересуясь в основном установлением количественного порядка и игнорируя тривиальный путь удвоения числа когерентных ортогональных сигналов, имеем , или . Пусть необходимая скорость передачи в системе составляет бит/с, что соответствует передаче бит за выделенный интервал времени . Ясно, что ортогональное кодирование битовых блоков такой длины может быть осуществлено с помощью сигналов, обеспечивая асимптотический выигрыш от кодирования . Тогда спектральная эффективность системы, т.е. скорость, приходящаяся на 1 Гц полосы, использующей ортогональные сигналы, будет

, (2.66)

откуда следует ее значительное уменьшение (почти экспоненциальное) с ростом желаемого выигрыша от кодирования.

Обратимся к характеристикам численного примера.

Пример. Для цифровых систем передачи речи очень типичной является скорость кбит/с (мобильная телефония, системы мультимедиа и др.). Предположим, что необходимо уменьшить в три раза (на 4.8 дБ) излучаемую мощность без потери в величине скорости. Если достижение поставленной цели осуществляется путем использования ортогональных сигналов, то это становится возможным лишь за счет снижения спектральной эффективности с 1 до 6/64, как следует из соотношения (2.66). Другими словами, для сохранения неизменной скорости кбит/с необходимо использовать полосу не менее чем 100 кГц. Эта цифра не является запредельной для многих приложений, так, например, на данном принципе строится обратный канал сотовой системы мобильной связи стандарта cdmaOne.

Представим теперь ситуацию, когда, основываясь на результатах успешно решенной предыдущей задаче, планируется достичь десятикратного (10 дБ) уменьшения излучаемой мощности. Реализация поставленной цели требует применения ортогональных сигналов для кодирования блоков длиной бит. Это приведет к спектральной эффективности, меньшей , или полосе, шире 480 МГц, что представляется совершенно неприемлемым при скорости в 9.6 кбит/с.

Вышеприведенное обсуждение свидетельствует об очень жестком характере обмена между энергетической и спектральной эффективностью, присущем ортогональному кодированию. В то же время уместно отметить, что, несмотря на значительный энергетический выигрыш, практически недостижимый при использовании ортогональных сигналов из-за неприемлемых требований к полосе, асимптотический выигрыш при ортогональном кодировании может служить хорошей отправной точкой, будучи верхней границей теоретической эффективности при любом методе кодирования – битовых блоков.

55