32. Множество многочленов от нескольких переменных над областью целостности.
Определение
1.1.
Многочленом
от переменных
над
областью целостности
называется выражение вида:
где
– элементы области целостности К. Их
называют коэффициентами многочлена
(1).
–
целые неотрицательные числа,
- члены многочлена .
Для
сокращения записей многочлены от
нескольких переменных будем обозначать
и т.д.
Множество
всех многочленов от n переменных
над областью целостности К будем
обозначать через
Определение
1.2.
Многочлены
и
из множества
называются равными,
если они состоят из одинаковых членов,
не учитывая члены с нулевыми коэффициентами.
Определение
1.3.
Суммой
подобных одночленов
будем называть одночлен
Определение
1.4. Суммой
многочленов
и
из множества
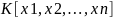называется
многочлен, который получается в результате
приписывания к многочлену
со знаком "+" многочлена
и приведения затем подобных членов.
Определение
1.5.
Произведением
одночленов
из множества
называется одночлен
Определение
1.6.
Произведением
многочленов
и
из множества
называется сумма произведений каждого
члена многочлена
на каждый член многочлена
.
33. Кольцо многочленов от нескольких переменных над областью целостности.
Теорема 1.1. Множество образует область целостности с единицей относительно операций сложения и умножения многочленов.
до-во: применим индукцию по n , то есть по числу переменных.
Для
n=1 теорема верна, так как множество
многочленов от одной
переменной над К образует область целостности.
Будем
полагать далее, что теорема верна для
n-1, то есть что
является областью целостности с единицей.
Очевидно,
что
является областью целостности над полем
К
.
до-но.
34. Степень многочлена от нескольких переменных.
Определение
2.1.
Степенью
многочлена
относительно переменной
называется максимальный показатель, с
которым
входит в члены многочлена с ненулевыми
коэффициентами.
Определение
2.2.
Степенью
одночлена
называется сумма показателей при
переменных в этом одночлене, то есть
сумма
.
Определение 2.3. Степенью многочлена f ≠ 0 называется максимальная из степеней его членов с ненулевыми коэффициентами.
Всякий элемент
является многочленом нулевой степени.
Для нулевого многочлена степень не определена.
Очевидно, что степень суммы многочленов не превосходит максимальной из степеней слагаемых многочленов.
5. Степень произведения многочленов.
Теорема: степень произведения многочленов и равна сумме степеней сомножителей.
До-во:
пусть степени многочленов
и
соответственно
равны
и
.
Сгруппировав все ненулевые члены
максимальной степени в многочленах
и
получим представление этих многочленов
в виде :
где
–
многочлен, все члены которого имеют
степень
;
многочлен, все
члены которого имеют степень
–
многочлен, степень которого меньше
– многочлен, степень которого меньше
Тогда
(4)
Очевидно, что все
члены многочлена
имеют
степень
Так как
– область целостности,
то из
и
следует, что
Итак, произведение
содержит
члены с ненулевыми коэффициентами
степени
.
Легко заметить, что все члены слагаемых
в
равенстве (4) имеют меньшую степень.
Отсюда следует, что степень произведения
равна
до-но.
Определение:
многочлен
называется однородным
многочленом или формой,
если все его члены имеют одинаковую
степень.
Однородный многочлен первой степени называется линейной формой, второй степени – квадратной формы, третьей степени – кубической формы.