25. Произведение двух многочленов с целыми коэффициентами.

Определение: многочлен f(x) с целыми коэффициентами называется примитивным, если НОД всех его коэффициентов равен 1.

Лемма 3. Произведение двух примитивных многочленов также является примитивным многочленом.

Лемма 4: если многочлен с целыми коэффициентами приводим над полем Q, то его можно представить в виде произведения двух многочленов с целыми коэффициентами, степень каждого из которых меньше степени многочлена .

до-во: т.к. f(x) – приводим, то его можно представить в виде , , , и - многочлены с рациональными коэффициентами.

Пусть – НОК всех знаменателей коэффициентов многочленов и , тогда , где – многочлены с целыми коэффициентами. Если 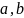– НОД коэффициентов многочленов , то , где – примитивные многочлены. При необходимости сократив дробь, представим её в виде , где , таким образом из делит все коэффициенты многочлена . По лемме 3 этот многочлен является примитивным ⇨ .

до-но.

26. Алгебраическая замкнутость поля.

Определение: поле Р называется алгебраически замкнутым, если всякий многочлен из кольца степени разлагается над полем Р в произведение линейных множителей.

Определение: поле Р называется алгебраически замкнутым, если всякий многочлен из степени имеет в поле Р хотя бы один корень.

Покажем, что определения эквивалентны. Пусть поле Р алгебраически замкнуто по первому определению:

, где - элементы поля Р ⇨ - это корни ⇨ Р алгебраически замкнуто по второму определению.

Пусть поле Р алгебраически замкнуто по второму определению, т.е. всякий многочлен из кольца имеет корень – корень

Поле Р алгебраически замкнуто по первому определению.

27. Основная теорема алгебры.

Определение: функция от комплексной переменной называется непрерывной в точке , когда для любого сколь угодно малого действительного числа существует , что удовлетворяющего неравенству будет выполнено неравенство , и 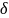- действительные .

Функция f(x) называется непрерывной, если она непрерывна в каждой точке области определения.

Лемма 1:всякий многочлен из кольца является непрерывной функцией.

Лемма 2: модуль многочлена из кольца является непрерывной функцией.

Следствие: если последовательность комплексных чисел сходится к , то

Следствие: если последовательность комплексных чисел сходится к , то , то

Лемма 3(Доломбера): пусть многочлен из кольца C[x], , если , то существует комплексное число C, что .

Лемма 4(о возрастании модуля многочлена): пусть - последовательность комплексных чисел такая что

Теорема (основная теорема алгебры): всякий многочлен из кольца степени имеет по крайней мере один комплексный корень.

до-во: Обозначим через M множество всех значений модуля многочлена f (x) . Пусть множество М всех значений модуля многочлена . Так как для любого C – комплексного , – неотрицательное действительное число, то множество M ограничено снизу. Из курса математического анализа известно, что всякое множество действительных чисел, ограниченное снизу, имеет точную нижнюю грань. Обозначим через l точную нижнюю грань множества M. Тогда, в частности, для любого натурального числа k можно подобрать такое комплексное число , что . Если бы было не так, то 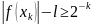, и l не было бы нижней гранью множества M. Из (1) следует . Если построенная последовательность комплексных чисел неограничена, то в ней можно выделить подпоследовательность, которая стремится к . . По лемме 4 что противоречит (2). ⇨ что последовательность ограничена. Тогда в ней можно выделить сходящуюся подпоследовательность, тогда по лемме 2

Если l ≠ 0 , то по лемме 3 существует такое комплексное число c, что .

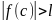Это противоречит тому, что l – точная нижняя грань множества M ⇨ l=0 и и ⇨ – комплексный корень.

до-но.