Эквивалентные величины Определение

Если , то бесконечно малые величины α и β называются эквивалентными ( ).

Очевидно, что эквивалентные величины являются частным случаем бесконечно малых величин одного порядка малости.

При справедливы следующие соотношения эквивалентности (как следствия из так называемых замечательных пределов):

• 

• 

• 

• 

• , где a > 0;

• 

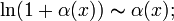
• , где a > 0;

• 

• 

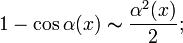
• , поэтому используют выражение:

, где .

Теорема

Предел частного (отношения) двух бесконечно малых величин не изменится, если одну из них (или обе) заменить эквивалентной величиной.

Данная теорема имеет прикладное значение при нахождении пределов (см. пример).

#35

Определение. Точка х₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х₀ или не является непрерывной в этой точке.

            Определение. Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х₀, достаточно того, что она определена слева и справа от нее.

Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.

Определение. Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

#39

Определения дифференциала

Для функций

Дифференциал функции в точке может быть определён как линейная функция

где f'(x₀) обозначает производную f в точке x₀.

Таким образом df есть функция двух аргументов .

Дифференциал может быть определён напрямую, т.е., без привлечения определения производной как функция линейно зависящая от h и для которой верно следующее соотношение

Для отображений

Дифференциалом отображения в точке называют линейный оператор такой, что выполняется условие

Дифференцируемость

Производная функции f в точке x₀, будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция f является дифференцируемой в точке x₀ тогда и только тогда, когда её производная в этой точке существует и конечна:

Для дифференцируемой в x₀ функции f в окрестности U(x₀) справедливо представление

при

#40

Частные производные. 2.1     Частные производные.         Частной производной функции нескольких переменных по какой-нибудь переменной в рассматриваемой точке называется обычная производная по этой переменной, считая другие переменные фиксированными (постоянными). Например, для функции двух переменных  в точке  частные производные определяются так: ,       ,      если эти пределы существуют. Величина                           называется частным                          приращением функции z в точке  по аргументу . Используются и другие   обозначения частных производных:             ,  ,      ,       ,             ,  ,      ,       .       Символы , , ,    как дроби трактовать нельзя (в этом отличие от случая одной переменной).       Из определения следует геометрический смысл частной производной функции двух переменных: частная производная  - угловой коэффициент касательной к линии пересечения поверхности   и плоскости                           в соответствующей точке.        Пользуясь понятием скорости изменения переменной, можно сказать, что частная производная  есть скорость изменения функции  относительно  при постоянном .        Из определения частных производных следует, что правила вычисления их остаются теми же, что для функций одной переменной, и только требуется помнить, по какой переменной ищется производная.

Полный дифференциал.        .                                              (1)       Если приращение (1) можно представить в виде        ,                                                        (2) Где Аи В не зависят от  и , а  и  стремятся к нулю при стремлении к нулю  и , то функция  называется дифференцируемой в точке , а линейная часть  приращения функции (т.е. та часть , которая зависит от   и  линейно) называется полным дифференциалом (или просто дифференциалом) этой функции в точке  и обозначается символом :                                    .                                                                      (3)       Из определения дифференцируемости функции следует, что если данная функция дифференцируема в точке , то она в этой точке непрерывна.       Действительно, если в точке  функция  дифференцируема, то для этой точки   представимо в форме (2), откуда следует, что                                    , а это и означает, что в точке  функция  непрерывна.       Из дифференцируемости функции в данной точке следует существование ее частных производных в этой точке (необходимое условие дифференцируемости).

#42

Во многих задачах функция  y(x) задана невным образом. Например, для приведенных ниже функций

невозможно получить зависимость y(x) в явном виде. Алгоритм вычисления производной  y'(x) от неявной функции выглядит следующим образом:

• Сначала необходимо продифференцировать обе части уравнения по отношению к x, предполагая, что y - это дифференцируемая функция x и используя правило вычисления производной от сложной функции;

• Решить полученное уравнение относительно производной  y'(x).

#44

Дифференциалы высших порядков

Введем понятие дифференциала высшего порядка. Полный дифференциал функции (формула (44.5)) называют также дифференциалом первого порядка.

Пусть функция z=ƒ(х;у) имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле (d²z = d(dz). Найдем его:

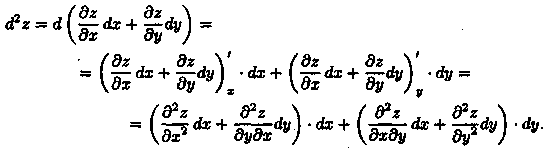
Отсюда: Символически это записывается так:

Аналогично можно получить формулу для дифференциала третьего порядка:

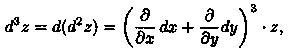
где

Методом математической индукции можно показать, что

Отметим, что полученные формулы справедливы лишь в случае, когда переменные х и у функции z = ƒ(х;у) являются независимыми.

№51-53