
- •Основные понятия
- •Скалярное произведение векторов и его свойства
- •7.1. Определение векторного произведения
- •7.2. Свойства векторного произведения
- •7.3. Выражение векторного произведения через координаты
- •7.4. Некоторые приложения векторного произведения
- •Смешанное произведение трех векторов и его свойства
- •Краткий конспект лекции 13
- •Глава 5. Элементарная теория линейных операторов (продолжение)
- •5.3. Сопряженный оператор
- •5.3.1. Сопряженный оператор и его матрица
- •5.3.2. Самосопряженный оператор
- •5.3.3. Собственные значения и собственные векторы самосопряженного оператора
- •5.3.4. Приведение матрицы линейного оператора к диагональной форме
- •Бесконечно малая величина
- •Бесконечно большая величина
- •Свойства бесконечно малых
- •Связь бесконечно малой и бесконечно большой величины
- •Сравнение бесконечно малых функций.
- •Эквивалентные величины Определение
- •Теорема
- •Локальные экстремумы
5.3.4. Приведение матрицы линейного оператора к диагональной форме
Таким образом можно описать алгоритм приведения матрицы линейного оператора к диагональной форме.
Он состоит в следующем:
записываем матрицу оператора A в исходном базисе;
записываем характеристическое уравнение и вычисляем его корни;
находим собственный базис оператора (если он существует);
записываем матрицу C, столбцами которой являются координаты собственных векторов (векторов собственного базиса);
по формуле C-1AC находим диагональную форму матриц оператора — матрицу оператора в собственном базисе.
#29-31
Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Бесконечно малая величина
Последовательность
an называется бесконечно
малой, если
![]() .
Например, последовательность чисел
.
Например, последовательность чисел
![]() —
бесконечно малая.
—
бесконечно малая.
Функция называется
бесконечно малой в окрестности точки
x0, если
![]() .
.
Функция называется
бесконечно малой на бесконечности,
если
![]() либо
либо
![]() .
.
Также бесконечно
малой является функция, представляющая
собой разность функции и её предела, то
есть если
![]() ,
то f(x) − a = α(x),
,
то f(x) − a = α(x),
![]() .
.
Бесконечно большая величина
Во всех приведённых
ниже формулах бесконечность справа от
равенства подразумевается определённого
знака (либо «плюс», либо «минус»). То
есть, например, функция xsin x,
неограниченная с обеих сторон, не
является бесконечно большой при
![]() .
.
Последовательность
an называется бесконечно
большой, если
![]() .
.
Функция называется
бесконечно большой в окрестности
точки x0, если
![]() .
.
Функция называется
бесконечно большой на бесконечности,
если
![]() либо
либо
![]() .
.
Свойства бесконечно малых
Сумма конечного числа бесконечно малых — бесконечно малая.
Произведение бесконечно малых — бесконечно малая.
Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.
Если an — бесконечно малая последовательность, сохраняющая знак, то
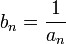 — бесконечно
большая последовательность.
— бесконечно
большая последовательность.
Пусть
![]() и
и
![]() бесконечно
большие величины при
бесконечно
большие величины при
![]() ,
т.е.
,
т.е.
![]() и
и
![]() .
.
1. Сумма бесконечно больших величин есть величина бесконечно большая:
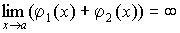 .
(4.20)
.
(4.20)2. Произведение бесконечно больших величин есть величина бесконечно большая:
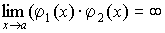 .
(4.21)
.
(4.21)3. Произведение бесконечно большой величины на константу С, или на функцию, имеющую конечный предел
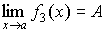 ,
есть величина бесконечно большая:
,
есть величина бесконечно большая: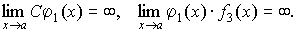 (4.22)
(4.22)Связь бесконечно малой и бесконечно большой величины
Величина, обратная бесконечно малой величине, есть величина бесконечно большая, и наоборот, величина, обратная бесконечно большой величине, есть величина бесконечно малая.
Пусть
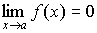 и
и
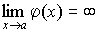 ,
тогда
,
тогда
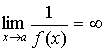 и
и
 .
.Символически можно записать:
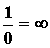 и
и
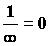
Сравнение бесконечно малых функций.
Пусть (х), (х) и (х) – бесконечно малые функции при х а. Будем обозначать эти функции , и соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
Например, функция f(x) = x10 стремится к нулю быстрее, чем функция f(x) = x.
Определение.
Если
![]() ,
то функция
называется бесконечно
малой более высокого порядка,
чем функция .
,
то функция
называется бесконечно
малой более высокого порядка,
чем функция .
Определение.
Если
![]() ,
то
и
называются бесконечно
малыми одного порядка.
,
то
и
называются бесконечно
малыми одного порядка.
Определение.
Если
![]() то
функции
и
называются эквивалентными
бесконечно малыми.
Записывают
~ .
то
функции
и
называются эквивалентными
бесконечно малыми.
Записывают
~ .
Пример. Сравним бесконечно малые при х0 функции f(x) = x10 и f(x) = x.
![]()
т.е. функция f(x) = x10 – бесконечно малая более высокого порядка, чем f(x) = x.
Определение.
Бесконечно малая функция
называется бесконечно
малой порядка k
относительно
бесконечно малой функции ,
если предел
![]() конечен
и отличен от нуля.
конечен
и отличен от нуля.
Однако следует отметить, что не все бесконечно малые функции можно сравнивать
между собой.
Например, если отношение
![]() не
имеет предела, то функции несравнимы.
не
имеет предела, то функции несравнимы.
