Скалярное произведение векторов и его свойства

М ы рассмотрели умножение вектора на число. Однако во многих задачах механики и физики встречается операция умножения вектора на вектор. Но при этом результат может быть как числом, так и вектором. Поэтому рассматривают два вида умножения векторов: скалярное и векторное.

Пусть даны два вектора и , угол между, которыми равен .

Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение обозначается . Итак, .

Если один из векторов нулевой, то угол не определен, и скалярное произведение по определения считается равным нулю.

Рассмотрим свойства скалярного произведения.

1. Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов и .

Очевидно, из определения скалярного произведения:

.

2. Для любого числа λ и любых векторов имеем:

.

Доказательство. Ограничимся случаем, когда λ > 0. В этом случае угол между векторами и совпадает с углом между векторами и , .

Поэтому . Откуда

Аналогично доказывается и равенство .

Случай λ <0 рассмотреть самостоятельно.

3. Для любых векторов выполняется равенство .

Доказательство. Используя определение скалярного произведения и свойства проекций вектора на ось, будем иметь

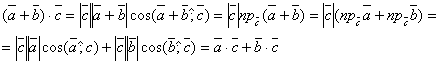
4. Для любого вектора выполняется соотношение .

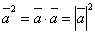Действительно, так как , то .

Из этого свойства в частности следует .

5. Скалярное произведение двух векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны.

Это свойство очевидно из определения скалярного произведения.

Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.

Итак, скалярное произведение векторов равно сумме произведений соответствующих координат: .

Это соотношение позволяет вычислить длину вектора через его координаты:

.

Далее из определения скалярного произведения находим

.

Выражая скалярное произведение и длины векторов через их координаты,получим формулу для нахождения косинуса угла между векторами

.

Условие ортогональности двух векторов:

или .

Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.

#12

7.1. Определение векторного произведения

Три некомпланарных вектора a, b и с, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).

     

 Векторным произведением вектора а на вектор b называется вектор с, который:

1. Перпендикулярен векторам a и b, т. е. са и сb;

2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е.

3.Векторы a, b и с образуют правую тройку.

Векторное произведение обозначается а х b или [а,b]. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j и k (см. рис. 18):

i х j = k,    j х k = i,    k х i = j. Докажем, например, что iхj=k.

1) ki, kj;

2) |k|=1, но | i x j| = |i| • |J| • sin(90°)=1;

3) векторы i , j и k образуют правую тройку (см. рис. 16).