
Глава III. Электромагнетизм
Магнитное действие тока. Магнитное взаимодействие токов. Закон Ампера. Рассмотрим магнитное взаимодействие тока. Она не зависит от заряда проводников, но сильно зависит от токов в них и сохраняется даже если 1 из проводников заэкранировать. Рассм взаимодействие в вакууме. Ампер установил, что сила взаимодействия проводников с током пропорциональна току в каждом из них. Но в случаях а) и б) магнитного взаимодействия не наблюдалось. (Рис) Ампер установил, что сила взаимодействия 2-х элементов тока (i*dl) обратно пропорциональна квадрату расстояния между ними и зависит от их ориентации. dF21 =

 или в векторной
ф-ме dF21
=
или в векторной
ф-ме dF21
=
 (Рис)
μ0
= 4π∙10^(-7) Гн/м
- абсолютная
магнитная проницаемость вакуума
(магнитная постоянная) В
законах магнитного
взаимодействия эл тока i∙dl
играет ту же роль, что и точечный
заряд в законах электростатики.
Пользуясь законом Ампера
можно вычислить силу взаимодействия
между эл-тами тока, на к-е можно разбить
любые замкнутые проводники, а
следовательно и силу взаимодействия
между этими проводниками. В
формуле dF21
и ее вект ф-ме з-н Ампера не удовлетворяет
3 з-ну Ньютона – в принципе отсутствует
слагаемое, которое обращается в 0 при
суммировании по замкнутому контуру.
(Рис)
μ0
= 4π∙10^(-7) Гн/м
- абсолютная
магнитная проницаемость вакуума
(магнитная постоянная) В
законах магнитного
взаимодействия эл тока i∙dl
играет ту же роль, что и точечный
заряд в законах электростатики.
Пользуясь законом Ампера
можно вычислить силу взаимодействия
между эл-тами тока, на к-е можно разбить
любые замкнутые проводники, а
следовательно и силу взаимодействия
между этими проводниками. В
формуле dF21
и ее вект ф-ме з-н Ампера не удовлетворяет
3 з-ну Ньютона – в принципе отсутствует
слагаемое, которое обращается в 0 при
суммировании по замкнутому контуру.
Магнитное поле. Вектор магнитной индукции. Закон Био-Савара-Лапласа. Вокруг проводников с током возникает магнитное поле.
Введем физическую
величину – индукцию
магнитного поля
(dB)
dB1=
![]() - Магн
индукция поля, создаваемого элементом
тока 1 в т нахождения эл-та тока 2.
Формула
для элементарного взаимодействия:
dF21
=
- Магн
индукция поля, создаваемого элементом
тока 1 в т нахождения эл-та тока 2.
Формула
для элементарного взаимодействия:
dF21
= ![]() В нек-й т с координатой r
эл-т i∙dl
создает
магнитную индукцию dB
dB1=
В нек-й т с координатой r
эл-т i∙dl
создает
магнитную индукцию dB
dB1=
![]() dB=
dB=
![]() -з-н
БиоСавара-Лапласа (Рис)
Для
магнитного поля справедлив принцип
суперпозиции: B
=
-з-н
БиоСавара-Лапласа (Рис)
Для
магнитного поля справедлив принцип
суперпозиции: B
= ![]() [B]
= 1
[B]
= 1 ![]() = 1
= 1![]() = 1 Тл Поле
магнитное изображают графически при
помощи линий индукции. Опыты показывают,
что линии магнитной индукции замкнуты
т.е. не имеют ни начала ни конца и
охватывают проводники с током. В силу
этого магнитное поле является вихревым.
Это объясняется тем, что магнитных
зарядов в природе нет. Направление
вектора В определяется по правилу
буравчика (правого винта)
(Рис)
= 1 Тл Поле
магнитное изображают графически при
помощи линий индукции. Опыты показывают,
что линии магнитной индукции замкнуты
т.е. не имеют ни начала ни конца и
охватывают проводники с током. В силу
этого магнитное поле является вихревым.
Это объясняется тем, что магнитных
зарядов в природе нет. Направление
вектора В определяется по правилу
буравчика (правого винта)
(Рис)
Магнитное поле прямого тока и кругового тока. Рассмотрим конечный проводник с током (Рис) По з-ну Б-С-Л: dB=

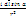 dl
=
dl
=  r
=
r
= Объединив
три последние формулы получим:
dB=
Объединив
три последние формулы получим:
dB=
 Интегрируем
по углу: B=
Интегрируем
по углу: B=
 =
=
 Для
решения задач удобно использовать
видоизмененную формулу (Рис)
Легко получить: B
=
Для
решения задач удобно использовать
видоизмененную формулу (Рис)
Легко получить: B
=
 где α1>0,
α2>0
От этого
частного случая перейдем к другому.
Пусть рассматриваемый
проводник
бесконечно длинный,
тогда θ1
=0 ,θ2
=π
Тогда ф-ла выродится в инд
магн поля бесконечно длинного проводника
прямого тока
(тока в прямых проводниках) B=
где α1>0,
α2>0
От этого
частного случая перейдем к другому.
Пусть рассматриваемый
проводник
бесконечно длинный,
тогда θ1
=0 ,θ2
=π
Тогда ф-ла выродится в инд
магн поля бесконечно длинного проводника
прямого тока
(тока в прямых проводниках) B=
 Рассмотрим
круговой ток: Рассмотрим участок
с эл-том тока i∙dl
dB=
Рассмотрим
круговой ток: Рассмотрим участок
с эл-том тока i∙dl
dB=
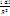 B=
B=
 =
=
 B
=
B
=
 -
круговой
ток (Аналог
Т.О-Г для магнитного поля)
-
круговой
ток (Аналог
Т.О-Г для магнитного поля)
Закон полного тока для магнитного поля в вакууме. Легко видеть, что магнитное поле пропорц току текущему по контуру или проводнику (Рис) Рассмотрим замкн контур L произвольной ф-мы, охватывающий беск длин прямолин проводник с током I. (Скал произв в-в):
 = B∙dl∙cos
θ
= Br
dφ
Вычислим циркуляцию в-ра B
по замкн контуру L
= B∙dl∙cos
θ
= Br
dφ
Вычислим циркуляцию в-ра B
по замкн контуру L
 =
= 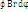 =
= 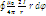 = μ0∙I
Можно опказать, что если контур
охватывает несколько токов произвольного
направления, то нужно взять их
алгебраическую сумму
= μ0∙I
Можно опказать, что если контур
охватывает несколько токов произвольного
направления, то нужно взять их
алгебраическую сумму 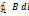 = μ0
= μ0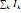 - з-н
полного тока
Циркуляция
в-ра магн индукции пост эл-го тока в
вакууме пропорциональна алг сумме
токов, охватываемых этим контуром.
(Рис) Если контур охватывает ток
дважды, то ставится коэф-т 2.
- з-н
полного тока
Циркуляция
в-ра магн индукции пост эл-го тока в
вакууме пропорциональна алг сумме
токов, охватываемых этим контуром.
(Рис) Если контур охватывает ток
дважды, то ставится коэф-т 2.
Магнитное поле тороида и длинного соленоида. Взаимодействие параллельных токов. Тороид – кольцевая катушка с током, витки к-й намотаны на сердечник имеющий форму тора. (Рис) N – витков, i – ток в витках. Применим з-н полн тока для средней линии тороида. B=const Циркуляция тогда: B∙2π∙r = μ0∙N∙i B =
 Обозначим n
=
Обозначим n
= 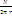 ч-ло витков на ед длины средней линии
тороида B
= μ0∙n∙i
n∙i
– число ампер-витков Если r1
и r2
близки друг к другу, то поле в
перпендикулярном сечении тороида
можно считать однородным. (Рис)
Станем неограниченно увеличивать
радиус тороида, тогда любой отрезов
тороида перейдет в прямую катушку или
– соленоид.
На оси такого соленоида: B
= μ0∙n∙i
Ф-ла справедлива для длинного
соленоида (длина >> диаметра) В центре
основания магн поле вдвое меньше.
По з-ну Ампера: dF
ч-ло витков на ед длины средней линии
тороида B
= μ0∙n∙i
n∙i
– число ампер-витков Если r1
и r2
близки друг к другу, то поле в
перпендикулярном сечении тороида
можно считать однородным. (Рис)
Станем неограниченно увеличивать
радиус тороида, тогда любой отрезов
тороида перейдет в прямую катушку или
– соленоид.
На оси такого соленоида: B
= μ0∙n∙i
Ф-ла справедлива для длинного
соленоида (длина >> диаметра) В центре
основания магн поле вдвое меньше.
По з-ну Ампера: dF Пусть поле однородное, тогда:
Пусть поле однородное, тогда:
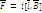 (Рис) Направление силы определяется
по правилу «левой
руки», т.е. 4 пальца по току, большой как
и F,
В – входит в ладонь.
Действие магн поля на ток используется
в электродвигателях и измерительных
приборах. Если имеются 2 прямых
параллельных тока, то можно показать,
что сила
действующая на отрезок проводника
(Рис):
F
=
(Рис) Направление силы определяется
по правилу «левой
руки», т.е. 4 пальца по току, большой как
и F,
В – входит в ладонь.
Действие магн поля на ток используется
в электродвигателях и измерительных
приборах. Если имеются 2 прямых
параллельных тока, то можно показать,
что сила
действующая на отрезок проводника
(Рис):
F
=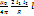
Действие магнитного поля на движущийся заряд. Сила Лоренца. dF
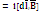 (Вект произвед) i∙dl
=
(Вект произвед) i∙dl
=  =
=  =
=  =
=  (
( = dN),
n
– конц-я, V
– ск-ть движения частицы с зарядом е,
dN
– ч-ло частиц n
в объеме Sdl.
d
= dN),
n
– конц-я, V
– ск-ть движения частицы с зарядом е,
dN
– ч-ло частиц n
в объеме Sdl.
d = dN
e[
= dN
e[ ]
Тогда сила, действующая на 1 частицу:
f
= e[
]
Тогда сила, действующая на 1 частицу:
f
= e[ ]
– сила Лоренца.
F=
eVB
sin(
]
– сила Лоренца.
F=
eVB
sin( )
f┴V
f┴dr
=Vdt
(Рис) 4 пальца по движению
+ частицы. (Если электрон – то 4 пальца
в обратн сторону) dA
= f
dr
= e[
)
f┴V
f┴dr
=Vdt
(Рис) 4 пальца по движению
+ частицы. (Если электрон – то 4 пальца
в обратн сторону) dA
= f
dr
= e[ ]
∙V
dt
= 0 Сила
Лоренца не меняет ск-ти движения по
величине, а меняет только лишь направление
ск-ти.
Рассм движениезаряда в однородн
поле. Сначала V┴B.
Сила Лоренца играет роль центростремительной
силы. eVB
=
]
∙V
dt
= 0 Сила
Лоренца не меняет ск-ти движения по
величине, а меняет только лишь направление
ск-ти.
Рассм движениезаряда в однородн
поле. Сначала V┴B.
Сила Лоренца играет роль центростремительной
силы. eVB
=  - центростремительная сила Лоренца.
(Рис) r
– радиус окружности. r
=
- центростремительная сила Лоренца.
(Рис) r
– радиус окружности. r
=  (Если по винтовой траектории, то
h
=VT)
Подсчитаем период обращения частицы
в магнитном поле. T
=
(Если по винтовой траектории, то
h
=VT)
Подсчитаем период обращения частицы
в магнитном поле. T
= T
=
T
=  T
=
T
=  Т.е. Т не зависит от ск-ти частицы, если
m=const.
Если угол между векторами v
и B
= α, то ск-ть частиц имеет 2 составляющие:
1- перпендикулярна в-ру В, 2 – параллельна
в-ру В. Такая частица движется по
спирали (Винтовая линия) Если
на движ эл заряд действует одновременно
электрические и магнитные поля, то
результирующая сила F
равняется:
Т.е. Т не зависит от ск-ти частицы, если
m=const.
Если угол между векторами v
и B
= α, то ск-ть частиц имеет 2 составляющие:
1- перпендикулярна в-ру В, 2 – параллельна
в-ру В. Такая частица движется по
спирали (Винтовая линия) Если
на движ эл заряд действует одновременно
электрические и магнитные поля, то
результирующая сила F
равняется:  = e∙
+ e[
= e∙
+ e[ ]
]
Эффект Холла. (Рис) Ч/з пластинку из золота пропускают пост ток i. Измеряется разность потенциалов φА – φС = ∆φ. Без магнитного поля ∆φ=0. При помещении пластинки в магн поле потенциалы φА и φС стали разными – Эффект Холла. В этом случае ∆φ = φА –φС = R
 , где
R
– постоянная Холла, зависит от a
и b.
Эффект Холла наблюдается во всех
проводниках и полупроводниках –
независимо от их материалов. С точки
зрения электронной теории носители
заряда под действием силы Лоренца
отклоняются к верхней грани. Возникает
поперечное электрическое поле, к-е в
дальнейшем препятствует отклонению
носителей. При равновесии сила
Лоренца: FЛ=
e∙E
e∙V∙B
= e∙E
E
=V∙B
Поскольку в опытах геометрические
размеры a<<b,
с - электрическое поле можно считать
однородным. φА
– φС
= E∙a
= V∙B∙a
Ток ч/з прямоугольную пластинку
i
= j∙S
= n∙e∙V∙a∙b
Объединив две полс ф-лы и исключив V:
φА
– φС
=
, где
R
– постоянная Холла, зависит от a
и b.
Эффект Холла наблюдается во всех
проводниках и полупроводниках –
независимо от их материалов. С точки
зрения электронной теории носители
заряда под действием силы Лоренца
отклоняются к верхней грани. Возникает
поперечное электрическое поле, к-е в
дальнейшем препятствует отклонению
носителей. При равновесии сила
Лоренца: FЛ=
e∙E
e∙V∙B
= e∙E
E
=V∙B
Поскольку в опытах геометрические
размеры a<<b,
с - электрическое поле можно считать
однородным. φА
– φС
= E∙a
= V∙B∙a
Ток ч/з прямоугольную пластинку
i
= j∙S
= n∙e∙V∙a∙b
Объединив две полс ф-лы и исключив V:
φА
– φС
= R
=
R
= -
постоянная Холла (е – носители заряда,
n
– конц носит заряда) Изменение
знака носителей заряда меняет направление
смещения этих зарядов. Одним из
важных применений эффекта Холла
является использование его в датчиках
измерения магн поля.
-
постоянная Холла (е – носители заряда,
n
– конц носит заряда) Изменение
знака носителей заряда меняет направление
смещения этих зарядов. Одним из
важных применений эффекта Холла
является использование его в датчиках
измерения магн поля.
Контур с током в магнитном поле. Магнитный момент витка с током. Рассмотрим прямоугольную рамку, помещенную в магнитное поле. (Рис) На каждый из проводников длиной а действуют силы либо сжимающие виток, либо растягивающие его. Если виток жесткий, то ими можно пренебречь. F = ibB Механический момент (М) : M = 2F =
 sin
α
= F∙a∙sin
α = i∙B∙a∙b∙sin
α
Назовем величину pm
= i∙S∙n
– магнитным
моментом
рамки с током. Объединив ф-лы (Ж
шрифт) получим
sin
α
= F∙a∙sin
α = i∙B∙a∙b∙sin
α
Назовем величину pm
= i∙S∙n
– магнитным
моментом
рамки с током. Объединив ф-лы (Ж
шрифт) получим 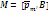 Следствие: Рамка
с током поворачивается в магн поле до
тех пор, пока векторы pm
и B
не станут параллельными друг другу.
Следствие: Рамка
с током поворачивается в магн поле до
тех пор, пока векторы pm
и B
не станут параллельными друг другу.
Магнитный поток. Магнитный поток сквозь малую площадку dS наз-ся величина dФm =
 = B∙dS∙cos
α = Bn
dS
(Рис)
= B∙dS∙cos
α = Bn
dS
(Рис)  магн поток ч/з площадку конечной
величины Фm
=
магн поток ч/з площадку конечной
величины Фm
=  =
= Если магн поле однородно, то Фm
=B∙S
Единица измерения : 1Вб
= 1В∙с
Можно доказать Т О-Г для магн поля:
=
= 0
Магн
поток сквозь произвольн замкн пов-ть
= 0.
Теорема отражает отсутствие в природе
магнитных зарядов, подобных электрическим.
Если магн поле однородно, то Фm
=B∙S
Единица измерения : 1Вб
= 1В∙с
Можно доказать Т О-Г для магн поля:
=
= 0
Магн
поток сквозь произвольн замкн пов-ть
= 0.
Теорема отражает отсутствие в природе
магнитных зарядов, подобных электрическим.
Работа при перемещении проводника и контура с током в магнитном поле. Т.к. на проводник с током в магнитном поле действует сила, при движении проводника совершается работа. Пусть прямой проводник длиной l с током i нах-cя в магнитном поле и совершает перемещение dr (Рис) = [
 ]
dA
=
]
dA
=  = i
[
]
= i
[
] = i
= i [
[ ]
; [
]=d
]
; [
]=d dA
= i
dA
= i = i
dФm
где dФm
–
магн поток сквозь ту площадку, к-ю
прочертил проводник (заметаемая
площадь) при своем движении в магн
поле. Т.е.
Фм
можно рассматривать, как приращение
магнитного потока, ч/з площадку ,
охватываемую некоторым контуром с
током. При этом контур
перемещается произвольно. Ток i
при этом должен оставаться неизменным.
При перемещении из
положения 1 в положение 2, работа: A12
=
= i
dФm
где dФm
–
магн поток сквозь ту площадку, к-ю
прочертил проводник (заметаемая
площадь) при своем движении в магн
поле. Т.е.
Фм
можно рассматривать, как приращение
магнитного потока, ч/з площадку ,
охватываемую некоторым контуром с
током. При этом контур
перемещается произвольно. Ток i
при этом должен оставаться неизменным.
При перемещении из
положения 1 в положение 2, работа: A12
=  = i
(Фm1
– Фm2)
Пусть
контур состоит из N
витков каждый из к-х пронизывается
магн потоком Фмк
, тогда ψ=
= i
(Фm1
– Фm2)
Пусть
контур состоит из N
витков каждый из к-х пронизывается
магн потоком Фмк
, тогда ψ=
 -
потокосмещение
Если
потоки ч/з отдельные витки одинаковы,
то ψ
= N∙Фm
Работа
при перемещении током контура выражается
ф-лой: A12
= i
(ψm1
– ψm2)
= iN(Фm1
– Фm2)
(Рис) Работа
по переворачиванию контура:
A
= iN(Фm2
– ( - Фm2))
= 2 i
N
Фm
= 2 i
N
BS
Во
всех случаях, работу совершает источник,
поддерживающий ток в контуре постоянным
-
потокосмещение
Если
потоки ч/з отдельные витки одинаковы,
то ψ
= N∙Фm
Работа
при перемещении током контура выражается
ф-лой: A12
= i
(ψm1
– ψm2)
= iN(Фm1
– Фm2)
(Рис) Работа
по переворачиванию контура:
A
= iN(Фm2
– ( - Фm2))
= 2 i
N
Фm
= 2 i
N
BS
Во
всех случаях, работу совершает источник,
поддерживающий ток в контуре постоянным
30. Явление
электромагнитной индукции. Опыты
Фарадея. Закон Фарадея-Максвелла.
Известно,
что электрич токи создают вокруг себя
магнитн поля. Как показал в 1831 году
Фарадей - магн поле может вызывать
появление электрических токов. (явление
электромагнитной индукции)
(Рис) Линии магнитного поля
являются замкнутыми (линии индукции),
появление тока в контуре I
Фарадей связал с фактом пересечения
линий индукции контуром I,
т.е. появление в контуре I
ЭДС связано со скоростью изменения
магнитного поля (магн потока) ч/з контур
I.
Тем самым была создана
теоретическая база для разработки
мощных источников электрической
энергии. Знак индукции тока
будет различным при размыкании и
смыкании контура II.
Определяется по
правилу Ленца:
Индукционный
ток во всех случаях направлен таким
образом, что его действие противоположно
действию причины, вызвавшей этот ток.
Возникновение индукц
тока в замкн контуре обусловлено
появлением в нем ЭДС, вызванное изменением
магн потока ч/з этот контур. Получим
выражение для ЭДС ч/з з-н сохр эн-и.
Пусть измеется замкнутый виток провода
и в него включена ЭДС – ε0
(≈ контур II)
Пусть виток движется в пост магн
поле. Магн силы совершают работу
i∙Фm,
одновременно выделяется тепло: (по
з-ну Джоуля Ленца) i2∙R∙dt,
Тогда работа гальванического эл-та:
ε0∙i∙dt
ε0∙i∙dt
= i2∙R∙dt
+ i∙Фm
i
= ![]() Дополнительное слагаемое в числителе
и есть ЭДС индукции ε
=
Дополнительное слагаемое в числителе
и есть ЭДС индукции ε
= ![]() - з-н
э/м индукции.
(знак “ - ” соответствует правилу Ленца)
ЭДС возникает либо при изменении
ф-мы контура, либо при его повороте,
либо при его перемещении, либо при
изменении со временем магн поля. Магн
поток : ∆Фm
= ∆B
∆S
∆cosθ
– что-то меняется – появляется ЭДС.
ЭДС в сложном контуре определяется
изменением потокосцепления ε
=
- з-н
э/м индукции.
(знак “ - ” соответствует правилу Ленца)
ЭДС возникает либо при изменении
ф-мы контура, либо при его повороте,
либо при его перемещении, либо при
изменении со временем магн поля. Магн
поток : ∆Фm
= ∆B
∆S
∆cosθ
– что-то меняется – появляется ЭДС.
ЭДС в сложном контуре определяется
изменением потокосцепления ε
= ![]()
Заряд, индуцированный при явлении электромагнитной индукции. Пусть магн поток, сцепленный с контуром изменяется от ψ1 до ψ2. Найдем заряд, к-й протекает при этом ч/з поперечное сечение контура: i =
 =
=  dq
=id
t
=
dq
=id
t
= 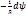 q
=
q
=  =
=  Протекший заряд не зависит от скорости
изменения потока. Ф-ла (Ж)лежит
в основе баллистического метода,
предложенного Столетовым для измерения
магнитной индукции. (Рис) Тогда
полный магнитный поток, сцепленный с
контуром (ψ1) будет равен: ψ1 = NBS,
N
– кол-во витков, b↑↑n
Повернем катушку на 180 градусов
относительно ее диаметра (Рис)
ψ2 = – ψ1 = – NBS
Тогда: ψ1 – ψ2 = 2ψ1
=
2NBS
Подставим: q
=
=
Протекший заряд не зависит от скорости
изменения потока. Ф-ла (Ж)лежит
в основе баллистического метода,
предложенного Столетовым для измерения
магнитной индукции. (Рис) Тогда
полный магнитный поток, сцепленный с
контуром (ψ1) будет равен: ψ1 = NBS,
N
– кол-во витков, b↑↑n
Повернем катушку на 180 градусов
относительно ее диаметра (Рис)
ψ2 = – ψ1 = – NBS
Тогда: ψ1 – ψ2 = 2ψ1
=
2NBS
Подставим: q
=
= Для баллистич гальванометра заряд
q
= CB∙n
n
– кол-во делений гальванометра, СВ
– постоянная баллистич гальванометра.
Приравн заряды: CB∙n
=
Для баллистич гальванометра заряд
q
= CB∙n
n
– кол-во делений гальванометра, СВ
– постоянная баллистич гальванометра.
Приравн заряды: CB∙n
= 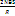 В =
В =  (число
2 обусловлено тем, что катушка
поворачивается на 180 градусов)
(число
2 обусловлено тем, что катушка
поворачивается на 180 градусов)
Явление самоиндукции. Индуктивность. Расчёт индуктивности для тороида. Электрический ток, текущий по контуру создает магн поток ψ ч/з этот контур. Если ток ч/з контур изменяется, то изменяется и поток ψ – явление самоиндукции. Потокосцепление всего контура - зависит от размеров контура, его ф-мы и магн св-в среды, окружающей контур. Известно, что В~i. Ψ= L∙i L – коэф-т – индуктивность контура (коэф-т самоиндукции) [L] = Гн На основании з-на э/м индукции можно записать: ε =
 =
=  Рассчитаем
индуктивность тороидальной катушки:
(Рис) S(поперечн
сеч) ,
l
– длина средн линии Все витки
обмотки хах-ся в одинаковых условия:
ψ = N∙Фm
= N∙B∙S
= N
Рассчитаем
индуктивность тороидальной катушки:
(Рис) S(поперечн
сеч) ,
l
– длина средн линии Все витки
обмотки хах-ся в одинаковых условия:
ψ = N∙Фm
= N∙B∙S
= N
 S
=
S
=  L
=
L
= 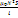 - индуктивность
Ф-ла годится и для длинного соленоида,
у к-го d
/ l
<<1.
- индуктивность
Ф-ла годится и для длинного соленоида,
у к-го d
/ l
<<1.
Токи при замыкании и размыкании цепи. Найдем з-н изменения тока в цепи с индуктивностью L и сопротивлением R при ее замыкании и размыкании, т.е. в неустановившемся режиме. Для тока в цепи: i =
 ε
=
ε
=  i
=
i
=  Разделим
переменные:
Разделим
переменные:  = ε0
– i∙R;
= ε0
– i∙R;
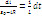 Проинтегрируем, преобразуем ln(ε0
-iR)
=
Проинтегрируем, преобразуем ln(ε0
-iR)
=  t
+ lnC
Потенциируя получим: ε0
– iR=
С∙
t
+ lnC
Потенциируя получим: ε0
– iR=
С∙ Для С – рассм нач усл при t=0,
i
=i0
из предыдущ ф-лы ε0
– i0R
= C
ε0
– iR=
(ε0
– i0R)
∙
Для С – рассм нач усл при t=0,
i
=i0
из предыдущ ф-лы ε0
– i0R
= C
ε0
– iR=
(ε0
– i0R)
∙ i=i0
∙
+
i=i0
∙
+ (
1 -
)
Выражение дает з-н изменения тока в
замкн цепи с пост R
и L
при включении в нее и выключении
источника ε0.
Рассм случай а) Замыкание цепи: i0=0
i
=
(
1 -
)
б)
размыкание цепи ε0
= 0 i
= i0∙
(Рис) Приближенно оценим ЭДС
самоиндукции, если сопротивление цепи
мгновенно увеличивается от r0
до R.
Пусть нач ток в цепи: i0
=
(
1 -
)
Выражение дает з-н изменения тока в
замкн цепи с пост R
и L
при включении в нее и выключении
источника ε0.
Рассм случай а) Замыкание цепи: i0=0
i
=
(
1 -
)
б)
размыкание цепи ε0
= 0 i
= i0∙
(Рис) Приближенно оценим ЭДС
самоиндукции, если сопротивление цепи
мгновенно увеличивается от r0
до R.
Пусть нач ток в цепи: i0
=  Спустя момент ток в цепи будет равен
i=
∙
+
(
1 -
) ε=
=
Спустя момент ток в цепи будет равен
i=
∙
+
(
1 -
) ε=
=  – 𝛆0
– 𝛆0
 =
=  Поскольку
Поскольку  >>
1 и при малых t
и больших L:
1 >
>>
1 и при малых t
и больших L:
1 >  t
>0 Следоват-но:
ε>>ε0 – При резком размыкании цепи
с большой индуктивность.
t
>0 Следоват-но:
ε>>ε0 – При резком размыкании цепи
с большой индуктивность.
Вихревые токи и скин-эффект. Явление взаимной индукции. Взаимная индуктивность тороида.
Индукционные токи могут возникать и в толще сплошных проводников при изменении в них магнитного потока (вихревые токи и токи Фуко). Это учитывается в конструкции трансформатора, сердечник к-го набирают из отдельных изолированных друг от друга пластин. Возникновение вихревых токов используется для э/м торможения в электроизмерительных приборах. Когда по проводам текут токи высокой частоты наличие вихревых токов приводит к вытеснению тока в целом к поверхности проводника. Такие токи текут в тонком слое вблизи поверхности (скин-эффект) Кроме того вихревые токи используются при закалке деталей и в электронных печах.
Явление взаимной
индукции
заключается в наведении ЭДС индукции
во всех проводниках, находящихся вблизи
цепи переменного тока. (Рис) Ток i1
создает потокосцепление в контуре 2,
пропорциональное току i1.
Ψ2=L21i1
. Если
ток i1
изменяется, то во 2м контуре возникает
ЭДС. ε2=
![]() Аналогично для контура 2.
Ψ1=L12i2
. ε1=
Аналогично для контура 2.
Ψ1=L12i2
. ε1=
![]() Контуры 1 и 2 наз-ют связанными.
L21=L12
– взаимная
индуктивность (Измеряют
в Гн -Генри), зависящая от формы, размеров,
взаимного расположения контуров,
магнитной проницаемости окружающей
среды. Рассматривают взаимную
индуктивность 2х обмоток N1
и N2,
взаимнонанесенных на тороидальный
сердечник, длина к-го l(длина
средней линии тороида), а толщина S
(площадь поперечного сечения) (Рис)
ψ2=
N2Фm1
= N2B1S
= N2μ0N1i1S/l
= μN1N2Si1/l.
Сравнивая с ф-лой Ψ2=L21i1
получим
L21=
L12
=
Контуры 1 и 2 наз-ют связанными.
L21=L12
– взаимная
индуктивность (Измеряют
в Гн -Генри), зависящая от формы, размеров,
взаимного расположения контуров,
магнитной проницаемости окружающей
среды. Рассматривают взаимную
индуктивность 2х обмоток N1
и N2,
взаимнонанесенных на тороидальный
сердечник, длина к-го l(длина
средней линии тороида), а толщина S
(площадь поперечного сечения) (Рис)
ψ2=
N2Фm1
= N2B1S
= N2μ0N1i1S/l
= μN1N2Si1/l.
Сравнивая с ф-лой Ψ2=L21i1
получим
L21=
L12
= ![]() - годится и для 2х соленоидальных
обмоток, если они длинные.
- годится и для 2х соленоидальных
обмоток, если они длинные.
Энергия магнитного поля. Объёмная плотность энергии. Рассм эл-ю схему: (Рис) После переброски ключа k в положение 2 ч/з сопротивление R некоторое время течет ток, поддерживаемый ЭДС самоиндукции. Очевидно, что соленоид L до переключения обладал энергией. Тогда работа тока за время dt: dA = iεdt = - Li
 dt
= - Lidi
A=
dt
= - Lidi
A=
 ,
Можно утверждать,что именно этой
энергией обладал соленоид: Wm
=
,
Можно утверждать,что именно этой
энергией обладал соленоид: Wm
=  ,
Сравним это выражение с ф-лой WK
=
,
Сравним это выражение с ф-лой WK
=  Инертные св-ва контура хар-ет
индуктивность L,
а роль скорости играет ток. Как
показывает опыт – эн-я контура
локализована в его магнитном поле
Wm=
Инертные св-ва контура хар-ет
индуктивность L,
а роль скорости играет ток. Как
показывает опыт – эн-я контура
локализована в его магнитном поле
Wm= ,
L
= (μ0N2S)/
l
, B
=μ0N∙i
/ l
Wm=
(μN2S∙B2l2)
/ (2∙l∙μ02∙N2
= B2S∙l2/
2∙μ0
= B2V
/ 2∙μ0
. Wm
=
,
L
= (μ0N2S)/
l
, B
=μ0N∙i
/ l
Wm=
(μN2S∙B2l2)
/ (2∙l∙μ02∙N2
= B2S∙l2/
2∙μ0
= B2V
/ 2∙μ0
. Wm
=  - энергия.
Объемная пл-ть эн-и магн поля: ωm
=
- энергия.
Объемная пл-ть эн-и магн поля: ωm
=
 ,
Если поле неоднородное, то
Wm
=
,
Если поле неоднородное, то
Wm
= 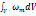 .
.
Магнитное поле в веществе. Микро- и макротоки. Вектор намагниченности. Мы полагали,что провода по к-м текут токи, находятся в вакууме. Если такие провода окружены средой, то магн поле в них будет другим. Каждое в-во явл-ся магнетиком , т.е. само намагничивается под действием магн поля, поэтому результирующее магн поле не равно 0, как поле в вакууме. Макротоками назовем электр токи проводимости, текущие по проводам, созданное ими магн поле – внешнее. Микротоки – токи, текущие в атомах и молекулах. Магн поле микротоков – внутреннее. Источником магн поля в вещ-ве сначала явл-ся макротоки. Очевидно, что в-р магн инд-и в вещ-ве будет зависеть от св-в вещ-ва. Каждый микроток создает магнитный момент, равный: pm= i∙S
 (S
(S =
= ).
При отсутствии внешн магн поля эти
микротоки ориентированы хаотически,
поэтому собственное магн поле не
создают. Во внешн магн поле их
расположение упорядочивается, возникает
внутреннее магн поле. Магн сост в-ва
характеризуют магн моментом единицы
его объема – вектором
намагниченности
).
При отсутствии внешн магн поля эти
микротоки ориентированы хаотически,
поэтому собственное магн поле не
создают. Во внешн магн поле их
расположение упорядочивается, возникает
внутреннее магн поле. Магн сост в-ва
характеризуют магн моментом единицы
его объема – вектором
намагниченности
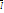
 Это осн величина, хар-ся магн сост
в-ва. Если в-р I
постоянен (
Это осн величина, хар-ся магн сост
в-ва. Если в-р I
постоянен ( =const),
то магн поле наз-ют – однородным:
[
]=A/м.
Аналогия
между эл и магн полями:
Силовой хар-кой электр поля явл-ся
напряженность E,
силовой хар-кой магн поля явл-ся индукция
В.
=const),
то магн поле наз-ют – однородным:
[
]=A/м.
Аналогия
между эл и магн полями:
Силовой хар-кой электр поля явл-ся
напряженность E,
силовой хар-кой магн поля явл-ся индукция
В.
Закон полного тока для магнитного поля в веществе. Для обобщения з-на полн тока в магнетике необходимо учесть как макротоки, так и микротоки.
 =μ0(i+iмикро)
Во второе слагаемое войдут только те
микротоки, к-е будут нанизаны на контур
L.
(Рис) Подсчитаем ∑ микротоков,
нанизанных на элемент dl.
n’
– число микротоков в единице объема.
i’n’dV
= i∙n’S
dl
cos
α
={i∙n’S=I}
=I∙dl
cos
α
={скал произв}=
∙dl
I
– намагниченность в-ва,
- в-р намагниченности. З-н
полн тока:
=μ0(i+iмикро)
Во второе слагаемое войдут только те
микротоки, к-е будут нанизаны на контур
L.
(Рис) Подсчитаем ∑ микротоков,
нанизанных на элемент dl.
n’
– число микротоков в единице объема.
i’n’dV
= i∙n’S
dl
cos
α
={i∙n’S=I}
=I∙dl
cos
α
={скал произв}=
∙dl
I
– намагниченность в-ва,
- в-р намагниченности. З-н
полн тока:
 =
μ0(i+
=
μ0(i+ )
)
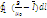 =i
, В-р
=i
, В-р  - напряженность
магн поля.
Тогда окончательно можно записать
- напряженность
магн поля.
Тогда окончательно можно записать
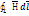 =
=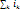 ; З-н
полного тока для диэлектриков в среде:
Циркуляция в-ра напряженности магн
поля вдоль произвольн замкн контура
= алгебраической сумме макротоков,
охватываемых этим конутром.
; З-н
полного тока для диэлектриков в среде:
Циркуляция в-ра напряженности магн
поля вдоль произвольн замкн контура
= алгебраической сумме макротоков,
охватываемых этим конутром.
Напряжённость магнитного поля. Изотропные магнетики. Относительная магнитная проницаемость. Величина Н (напряженность) является аналогом электрического смещения. Т.е. это вспомогательная физическая величина, к-ю нельзя измерить, но можно рассчитать. Она определяет внешнее магн поле, создаваемое макротоками. I=0 в вакууме. H=B/μ0. [H]=А/м Из ф-лы:
 можно получить: B=
μ0(H+I).
Пусть рассматриваемые магнетики
явл-ся
изотропными,
т.е. их магн св-ва не зависят от
направления. Опыты показывают,
что I=ǽmH,
ǽm
– магнитная восприимчивость в-ва(каппа),
B
= μ0(H+ǽmH)=
μ0∙
(1+ǽm)H
= μ0∙μ∙H
= B,
μ
= 1+ǽm
– относительная магнитная проницаемость
среды. Все формулы, полученные ранее
для магн поля в вакууме годятся для
изотропных магнетиков, если в них
вместо μ0
подставить μ0μ.
можно получить: B=
μ0(H+I).
Пусть рассматриваемые магнетики
явл-ся
изотропными,
т.е. их магн св-ва не зависят от
направления. Опыты показывают,
что I=ǽmH,
ǽm
– магнитная восприимчивость в-ва(каппа),
B
= μ0(H+ǽmH)=
μ0∙
(1+ǽm)H
= μ0∙μ∙H
= B,
μ
= 1+ǽm
– относительная магнитная проницаемость
среды. Все формулы, полученные ранее
для магн поля в вакууме годятся для
изотропных магнетиков, если в них
вместо μ0
подставить μ0μ.
Условия на границе раздела двух магнетиков. (Рис) Вычислим магн поле ч/з пов-ть такого замкнутого цилиндра. Он будет= 0, т.к. внутри нет токов. B2n∙S –B1n∙S=0, Нормальные составляющие в-в индукции на границе раздела непрерывны. B2n=B1n. Зная связь в-в Н и В получим μ0μ2∙Н2n = μ0μ1∙H1n . H2n / H1n = μ1 / μ2. Нормальные составляющие в-в напряженности терпят разрыв. По аналогии с эл-м полем получим для тангенсальных составляющих: H2t = H1t, B2t / μ0μ2 = B1t / μ0μ1 B2t / B1t = μ2 / μ1. Можно показать,что на границе раздела магнетиков линии магн инд-и преломляются. (Рис) tg α2 / tg α1 = μ2 / μ1. Из ф-лы следует, что при переходе в среду с большим значением μ линии магн индукции сильно отклоняются от нормали, т.е. – сгущаются. (Рис) Магн поле в замкнутом объеме много меньше, чем снаружи, но не равно нулю.
Типы магнетиков. Элементарная теория диа- и парамагнетизма. Условно все магнетики можно разделить на диамагнетики (μ<1), парамагнетики (μ>1) и ферромагнетики (μ>>1). ǽm<0, I ↑↓H - диамагнетики, ǽm>0 , i↑↑H – парамагнетики, Примеры диамагнетиков: - инертные газы, H2, N2, Zn, Cu, Au, Ag, Si, H20, германий, висмут, органич и неорганич соед; парамагнетиков: многие щелочные и щелочноземельные Ьу и сплавы, О2, NO, MgO, FeCl2 и др. Их общее качество (диа и пара): они намагничиваются очень слабо μ≈1. Магнитные св-ва тел обусловлены движением эл зарядов в их атомах и молекулах. Вычислим механич мом-т импульса эл-на: (Рис) Lm = m∙V∙r Такой эл-н можно рассматривать, как круговой ток и расситать магн момент его орбитального движения. pm= i∙S = e∙π∙r2/τ = e∙V∙π∙r2 / 2∙π∙r = ½ eVr pm= ½ eVr составим гиромагнитное отношение (магн мом-т к мех-му) pm / Lm = e∙V∙r / 2∙m∙V∙r = e/2∙m. Для разных орбит электронов в атоме это отношение остается постоянным. Как показывает теория строения атома стационарным орбитам соответствует момент импульса: LM,n = n * h/2π , где h – постоянная Планка ( h=6,62*10^(-34) Дж*с ), n – число из нат ряда(1,2,3…) Из 2х посл ф-л следует pm =n∙e∙h / 4∙π∙m μБ = e∙h / 4∙π∙m , μБ – магнетрон Бора – единица измерения магнитного момента электронных орбит. Рассмотрим изменение вращения эл-на по орбите и магн момента во внешнем магн поле. Пусть магн поле однородно, а пл-ть вращ эл-на ┴ к нему. (Рис) Кулоновская сила играет в отсутствие внешнего поля роль центростремительной силы. В случае, как было показано: pm(0) = ½ e∙V0r (H=0) Во внешнем поле Н действует кроме того сила Лоренца: FЛ = e∙V∙B = e∙V∙μ0∙H = μ0∙e∙V∙H В данном случае она направлена к оси вращения, тогда по 2 з-ну Ньют:
 =
=
 + μ0e∙V∙H
(*)
H=0,
+ μ0e∙V∙H
(*)
H=0,
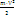 =
(**)
Вычтем
из (**)выражение
(*)
V2
- V02
=
=
(**)
Вычтем
из (**)выражение
(*)
V2
- V02
= 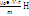 V2
– V02
= (V
+V0)(V-V0)≈2V(V
–V0)
(***)
Подставим (***) в предыдущее V-V0
=
V2
– V02
= (V
+V0)(V-V0)≈2V(V
–V0)
(***)
Подставим (***) в предыдущее V-V0
=  Подсчитаем изменение орбитального
момента: ∆pm=pm-pm(0)
= e∙r
/ 2 * (
)
=
Подсчитаем изменение орбитального
момента: ∆pm=pm-pm(0)
= e∙r
/ 2 * (
)
= 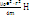 Аналогичный рез-тат получится,если
электрон будет вращаться в противоположном
направлении. При любом направлении
вращения эл-на вектор ∆pm
направлен против в-ра H.
(Рис) Проэкция pm
на H
есть pmcosθ.
У разных атомов эта проэкция различна,
поэтому
Аналогичный рез-тат получится,если
электрон будет вращаться в противоположном
направлении. При любом направлении
вращения эл-на вектор ∆pm
направлен против в-ра H.
(Рис) Проэкция pm
на H
есть pmcosθ.
У разных атомов эта проэкция различна,
поэтому  ≠0. Как показал Ланжевен в неслишком
сильных полях:
≠0. Как показал Ланжевен в неслишком
сильных полях:  =
=  Тогда намагниченность
парамагнетика:
I
= n∙pm∙
=
Тогда намагниченность
парамагнетика:
I
= n∙pm∙
=
 ǽm=
ǽm= Оценим ǽm
для газов-парамагнетиков: pm
μБ
=9,3*10^(-24) А*м2
;
n=2,7*10^25
м^(-3), T≈300
k,
ǽm=2?3*10^(-7)
ǽm
у диамагнетиков от температуры не
зависит, а у парамагнетиков уменьшается
при повышении Т ~1/T.
Оценим ǽm
для газов-парамагнетиков: pm
μБ
=9,3*10^(-24) А*м2
;
n=2,7*10^25
м^(-3), T≈300
k,
ǽm=2?3*10^(-7)
ǽm
у диамагнетиков от температуры не
зависит, а у парамагнетиков уменьшается
при повышении Т ~1/T.
Ферромагнетизм. Опыты Столетова. Кривая намагниченности. Магнитный гистерезис. У ферромагнетиков μ порядка 100 и 1000, поэтому это сильно намагничивающиеся в-ва. К ферромагн относятся все сплавы на осн железа, co,Ni и др. Для ферромагнетиков существ сложн нелинейная зав-ть между в-м В и в-м Н(Установлено Столетовым). В ее основе лежит зав-ть в-ра I от Н. (3 Рис). При Н→0 и μ→1, ǽm→0, т.к. μ=1+ǽm. Поместим внутрь катушки первоначально ненамагниченный ферромагнетик и станем увеличивать напряженность внешнего магнитного поля. (Рис) В0 –остаточная индукция(в этом сост он явл-ся пост магнитом) НК – коэрцитивная сила, характеризующая спос-ть материала сохранять намагниченное состояние. Замкнутая кривая АВ0СА – петля гистерезиса. ОА – кривая первоначального намагничивания. Магнитный гистерезис есть своеобразное отставание изменения индукции В от изменения напряженности Н. Индукция в кажд т определяется не только соотв полем Н, но и зависимостью от состояния предыдущего намагничивания. Магнитный гистерезис – в сильнейшей степени зависит от состава магнетика и его обработки. Так у мягкого железа петля гистерезиса узкая, у закаленной стали – широкая. Ширина петли гистерезиса определяет потери на перемагничивание, приводящие к нагреву ферромагнетика.
Домены. Точка Кюри. Спиновая природа ферромагнетизма. Согласно современной теории ферромагнетизма – магн св-ва определяются не орбитальными моментами эл-нов, а их спинами. Спин – собственный момент импульса частицы и соответствующий ему собственный магнитный момент pms. Гиромагнитное отношение спиновых магнитного и мех-го моментов для эл-на pms / Lms = e/m, т.к. Ls = ½ h /2π , то pms = e∙h/ 4π∙m = μБ. При опред условиях в кристаллах возникают т наз. обменные силы, к.е. заставляют спины эл-нов выстраиваться одинаково (самопроизвольное намагничивание). Образуются домены (небольшие области, которые поляризованы до насыщения, самопроизвольно намагничены). (Рис) Размеры доменов – 1-10 мк м. Рассмотрим кусок ферромагнетика. В слабых полях происходит смящения границ доменов. Ув-ся домены типа 1 и 5, ум-ся домены типа 2,3,4. В средних полях магн моменты доменов поворачиваются в направлении поля. В сильных полях после полной ориентации всех доменов происходит т.наз. паропроцесс – окончательная ориентация нек-х спинов. При ув-и напряж-ти поля имеющиеся в образце инородные включения и дефекты мешают плавному изменению границ доменов. Это приводит к скачкообразному изменению намагниченности и индукции при плавном изменении напряженности – эффект Баркгаузена. (Рис) Для каждого ферромагнетика существует температура, наз температура Кюри, при превышении к-й он превращается в парамагнетик. ТК = 768 С – железо, ТК = 365 С – никель. Ферромагнетизм – св-во коллектива атомов, в газообразном сост атом железа диамагнетен (μ<1). Магнитные материалы делятся на магнитомягкие и магнитотвердые(магнитожесткие). Широко применяются ферриты – сплавы из неферромагнитных мат-в, обладающие сильным ферромагнетизмом. У них наряду с высоким значением μ большое удельное сопротивление и их можно применять на высоких частотах. Для каждого ферромагнитного материала при расчете индукции пользуются известной зависимостью В(Н): Рассчитывают сначала напряженность Н. (Рис)
