8346
.docxВариант 1
КОНТРОЛЬНАЯ РАБОТА 1
106. Точка
движется по прямой согласно уравнению
х =
Аt +
Вt3,
где А =
6 м/с; В =
–0,125 м/с3.
Определите среднюю путевую скорость 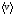 точки в интервале времени от t1 =
2 с до t2 =
6 с.
точки в интервале времени от t1 =
2 с до t2 =
6 с.
Решение. Скорость материальной точки

Приравняем скорость к нулю:
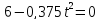
Отсюда находим момент времени, при котором скорость равна нулю, т.е. момент, когда точка меняет своё направление движения:
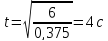
Как
видно t1 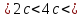 t2 =
6 с
t2 =
6 с
Путь,
пройденный точкой в интервале времени
t1 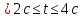 , равен
, равен
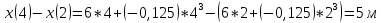
Путь,
пройденный точкой в интервале времени
4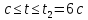 , равен
, равен
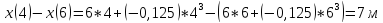
Тогда искомая средняя путевая скорость
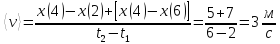
Ответ:
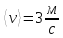
109. С высоты h = 2 м на стальную плиту свободно падает шарик массой m = 200 г и подпрыгивает на высоту h1 = 0,5 м. Определите импульс p, полученный шариком при ударе.
Решение.
Закон сохранения энергии (потенциальная
энергия, которой обладает шарик на
высоте
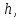 при падении переходит в кинетическую
энергию):
при падении переходит в кинетическую
энергию):
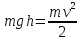
Где
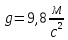 – ускорение
свободного падения
– ускорение
свободного падения
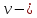 скорость
шарика в момент удара при падении
скорость
шарика в момент удара при падении

Далее
шарик отскакивает со скоростью
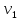 и
подпрыгивает на высоту h1 .
В этом случае закон сохранения энергии
и
подпрыгивает на высоту h1 .
В этом случае закон сохранения энергии
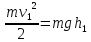
Отсюда
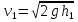
Соответственно импульс шарика уменьшается на величину
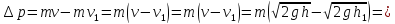
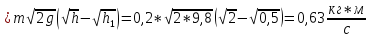
Ответ:

119. Шар массой m1 = 1 кг движется со скоростью v1 = 4 м/с и сталкивается с шаром массой m2 = 2 кг, движущимся навстречу со скоростью v2 = 3 м/с. Каковы скорости U1 и U2 шаров после удара? Удар считайте абсолютно упругим, прямым, центральным.
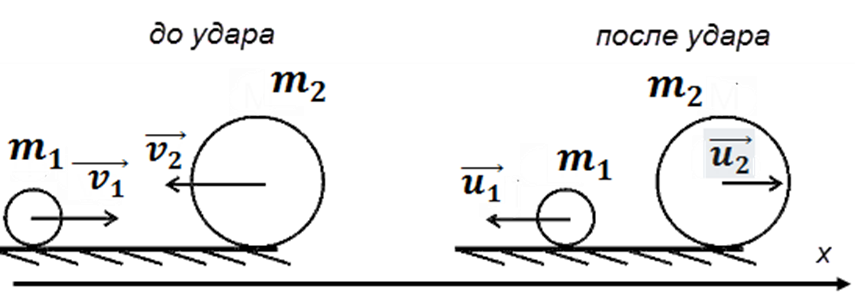
Решение.
Закон сохранения импульса в векторной форме
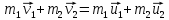
Закон сохранения импульса в проекциях на ось x
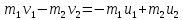

Закон сохранения энергии (справедлив при упругом ударе)
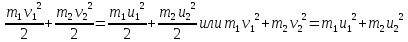
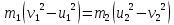
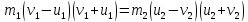
Делим
это уравнение на
 :
:
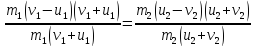

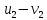

Подставим
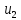 в закон сохранения импульса
в закон сохранения импульса

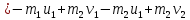
Отсюда находим скорость первого шара после удара

Скорость второго шара после удара
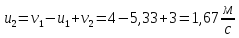
Ответ:
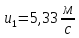
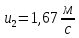
138. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмётся на ΔL = 3 мм. На сколько сожмёт пружину тот же груз, упавший на конец пружины с высоты h = 8 см?
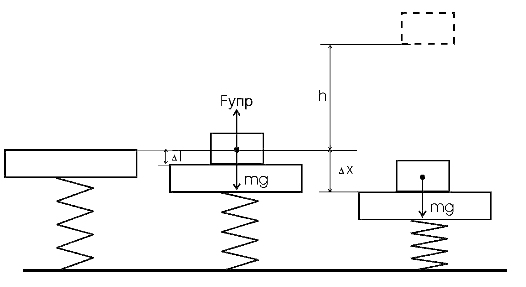
Решение. Сила упругости

Где
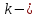 коэффициент
жёсткости пружины
коэффициент
жёсткости пружины
По третьему закону Ньютона в данном случае сила упругости равна силе тяжести
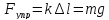
Где
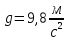 – ускорение свободного падения
– ускорение свободного падения
Отсюда
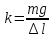
На
высоте
 груз обладает потенциальной энергией,
равной
груз обладает потенциальной энергией,
равной
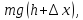 которая
при падении груза по закону сохранения
энергии равна энергии сжатой пружины,
т.е.
которая
при падении груза по закону сохранения
энергии равна энергии сжатой пружины,
т.е.
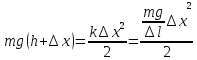
После преобразований получаем квадратное уравнение

Решение этого уравнения

По
здравому смыслу
 значит
значит
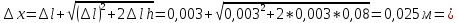
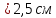
Ответ:
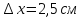
144. Нить с привязанными к её концам грузами массами m1 = 50 г и m2 = 60 г перекинута через блок диаметром D = 4 см. Определите момент инерции I блока, если под действием силы тяжести грузов он получил угловое ускорение β = 1,5 рад/с2.
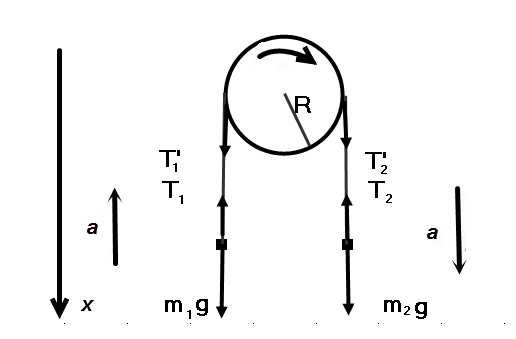
Решение. Второй закон Ньютона для грузов в векторной форме:
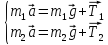
Второй закон Ньютона для грузов в проекциях на ось Х:
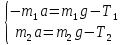
Согласно основному закону динамики вращательного движения момент сил, действующих на блок, равен
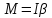
Где
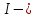 момент инерции блока
момент инерции блока
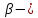 угловое
ускорение диска, которое связано с
линейным ускорением грузов
угловое
ускорение диска, которое связано с
линейным ускорением грузов
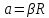
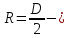 радиус
блока
радиус
блока
Силы
натяжения нитей действуют не только на
грузы, но и на диск и по третьему закону
Ньютона
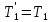 и
и

Вращающий момент сил натяжения

Таким образом,
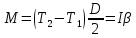
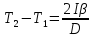
Имеем систему трёх уравнений с тремя неизвестными
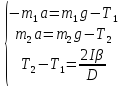
Выразим силы натяжения из первых двух уравнений и подставим в третье
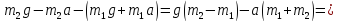
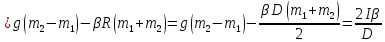
Отсюда момент инерции блока
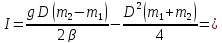
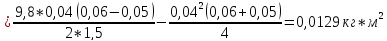
Ответ:
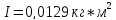
150. На краю неподвижной скамьи Жуковского диаметром D = 0,8 м и массой m1 = 6 кг стоит человек массой m2 = 60 кг. С какой угловой скоростью ω начнёт вращаться скамья, если человек поймает летящий на него мяч массой m = 0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии r = 0,4 м от оси скамьи. Скорость мяча v = 5 м/с.
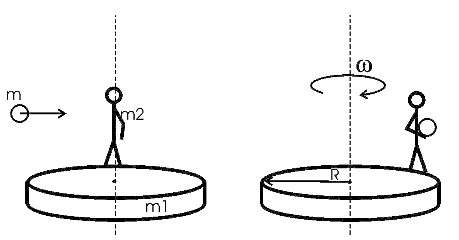
Решение. По закону сохранения момента импульса относительно оси вращения
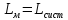
Где
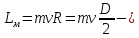 момент импульса мяча относительно
оси вращения
момент импульса мяча относительно
оси вращения
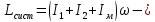 момент импульса
системы “скамья-человек-мяч ” относительно
оси вращения
момент импульса
системы “скамья-человек-мяч ” относительно
оси вращения
Где
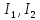 и
и
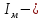 моменты
инерции соответственно скамьи Жуковского,
человека и мяча относительно оси вращения
моменты
инерции соответственно скамьи Жуковского,
человека и мяча относительно оси вращения
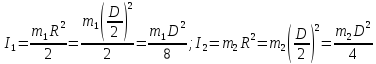
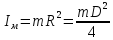
Итак,
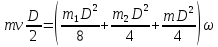
После преобразований
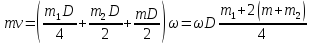
Отсюда искомая угловая скорость

Ответ:
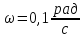
157. Определите напряжённость G гравитационного поля на высоте h = 1000 км над поверхностью Земли. Считайте известным ускорение g свободного падения у поверхности Земли и её радиус R.
Решение. Напряжённость гравитационного поля равна
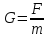
Где
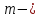 масса
притягиваемого тела
масса
притягиваемого тела
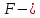 сила
притяжения тела к Земле, равная по закону
всемирного тяготения (закону Ньютона)
сила
притяжения тела к Земле, равная по закону
всемирного тяготения (закону Ньютона)
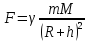
Где
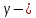 гравитационная
постоянная
гравитационная
постоянная
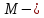 масса
Земли
масса
Земли
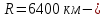 радиус
Земли
радиус
Земли
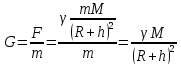
Нам известна напряжённость гравитационного поля у поверхности Земли
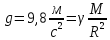
Отсюда

Поэтому

Ответ:
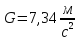
166. Определите период Т колебаний стержня длиной L = 30 см около горизонтальной оси, перпендикулярной стержню и проходящей через его конец.
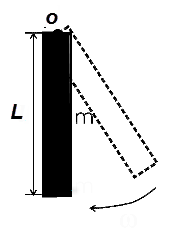
Решение. Колеблющийся стержень представляет собой физический маятник. Период малых колебаний физического маятника
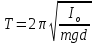
Где
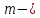 масса
маятника
масса
маятника
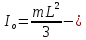 момент
инерции стержня относительно горизонтальной
оси, проходящей через точку подвеса О
момент
инерции стержня относительно горизонтальной
оси, проходящей через точку подвеса О
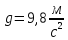 – ускорение
свободного падения
– ускорение
свободного падения
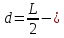 расстояние
от центра масс стержня до точки подвеса
О
расстояние
от центра масс стержня до точки подвеса
О
Итак,

Ответ:
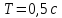
174. Складываются два колебания одинакового направления и одинакового периода: x1 = А1 sinω1t и x2 = А2sinω2(t + τ), где А1 = А2 = 3 см; ω1 = ω2 = π с–1; τ = 0,5 с. Определите амплитуду А и начальную фазу φ результирующего колебания. Напишите его уравнение. Постройте векторную диаграмму для момента времени t = 0.
Решение. Уравнение результирующего колебания при сложении двух колебаний одинакового направления и периода
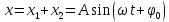
Где амплитуда результирующего колебания

В
данном случае
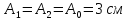 , начальные фазы колебаний по условию
задачи
, начальные фазы колебаний по условию
задачи
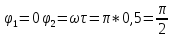 , так что
, так что
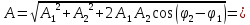

Начальная фаза результирующего колебания
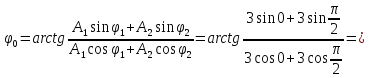

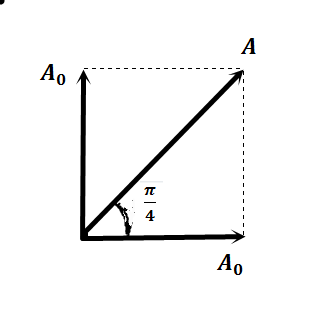
Таким образом
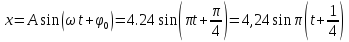
Векторная диаграмма сложения амплитуд на рисунке
КОНТРОЛЬНАЯ РАБОТА 2
202. Сколько атомов содержится в ртути: 1) количеством вещества ν = 0,2 моль; 2) массой m = 1 г?
Решение. 1)Искомое количество атомов
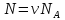
Где
 число
Авогадро
число
Авогадро
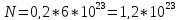
2) Искомое количество атомов

Где
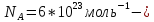 число
Авогадро
число
Авогадро
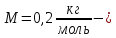 молярная
масса ртути
молярная
масса ртути
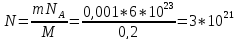
Ответ:
1)
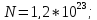 2)
2)
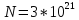
212. Вычислите плотность ρ азота, находящегося в баллоне под давлением p = 2 МПа и имеющего температуру Т = 400 К.
Решение. Уравнение Менделеева-Клапейрона
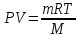
Где
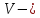 объём баллона
объём баллона
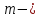 масса
азота
масса
азота
R универсальная
газовая постоянная
универсальная
газовая постоянная
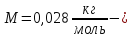 молярная
масса азота
молярная
масса азота
Отсюда плотность азота
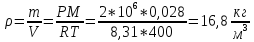
Ответ:
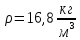
226. Количество вещества гелия ν = 1,5 моль, температура Т = 120 К. Определите суммарную кинетическую энергию Ек поступательного движения всех молекул этого газа.
Решение. Средняя кинетическая энергия поступательного движения одной молекулы газа
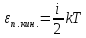
Где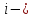 число
степеней свободы,
число
степеней свободы,
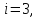 т.к.
гелий – одноатомный газ
т.к.
гелий – одноатомный газ
 – постоянная
Больцмана
– постоянная
Больцмана
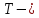 температура
газа
температура
газа
Общее количество молекул
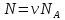
Где
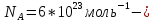 число
Авогадро
число
Авогадро
Соответственно суммарная кинетическая энергия поступательного движения всех молекул этого газа
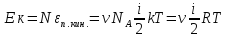
Где
R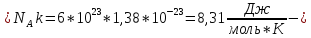 универсальная
газовая постоянная
универсальная
газовая постоянная
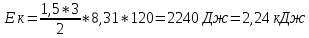
Ответ:
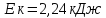
234. Определите относительную молекулярную массу Мr и молярную массу μ газа, если разность его удельных теплоёмкостей cp – cV = 2,08 кДж/(кг К).
Решение. Связь между удельной и молярной теплоемкостями при постоянном давлении:
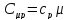
Аналогично связь между удельной и молярной теплоемкостями при постоянном объёме:
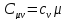
Уравнение Майера:
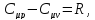
где
R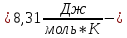 универсальная
газовая постоянная
универсальная
газовая постоянная
Или
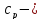

По
условию задачи
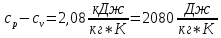
Тогда молярная масса газа
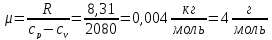
Этот
газ – гелий. По определению
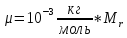
Поэтому
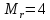
Ответ:

250. Найдите
среднюю длину свободного пробега
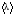 молекулы азота в сосуде объёмом V =
5 л. Масса газа m =
0,5 г.
молекулы азота в сосуде объёмом V =
5 л. Масса газа m =
0,5 г.
Решение. Средняя длина свободного пробега молекулы азота
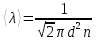
Где
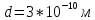 - эффективный диаметр молекулы азота
- эффективный диаметр молекулы азота
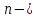 число
молекул в единице объёма, которое можно
найти из основного уравнения
молекулярно-кинетической теории:
число
молекул в единице объёма, которое можно
найти из основного уравнения
молекулярно-кинетической теории:
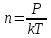
Где
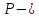 давление
газа
давление
газа
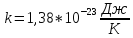 – постоянная
Больцмана
– постоянная
Больцмана
 температура
газа
температура
газа
Уравнение Менделеева-Клапейрона
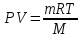
Где
R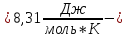 универсальная
газовая постоянная
универсальная
газовая постоянная
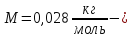 молярная
масса азота
молярная
масса азота
Отсюда
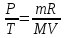
Тогда искомая средняя длина свободного пробега молекулы азота
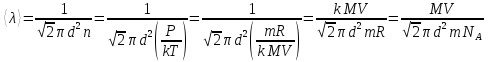
Здесь
R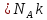
Где
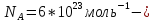 число
Авогадро
число
Авогадро
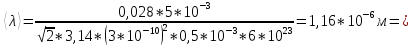

Ответ:
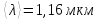
257. При адиабатном сжатии давление воздуха было увеличено от p1 = 50 кПа до p2 = 0,5 МПа. Затем при неизменном объёме температура воздуха была понижена до первоначальной. Определите давление p3 газа в конце процесса.
Решение.
Адиабатическое сжатие
Уравнение Пуассона для адиабатического процесса:
P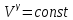 ,
,
Где
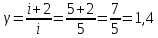 – показатель адиабаты
– показатель адиабаты
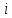 -
число степеней свободы, так как в воздухе
преобладают азот и кислород - двухатомные
газы, то
-
число степеней свободы, так как в воздухе
преобладают азот и кислород - двухатомные
газы, то
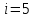
Таким образом,
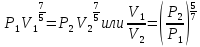
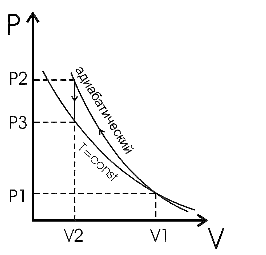
Так
как начальная и конечная точки лежат
на изотерме
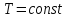 (так как в условии сказано, что начальная
и конечная температура равны), то из
уравнения изотермы
(так как в условии сказано, что начальная
и конечная температура равны), то из
уравнения изотермы
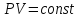 получаем:
получаем:
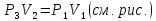
Тогда искомое давление
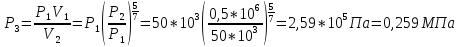
Ответ:
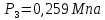
270. Идеальная тепловая машина работает по циклу Карно. Пусть температура Т1 нагревателя равна 500 К, температура холодильника Т2 = 250 К. Определите термический коэффициент полезного действия η цикла, а также работу W1 рабочего вещества при изотермическом расширении, если при изотермическом сжатии совершена работа W2 = 70 Дж.
Решение.
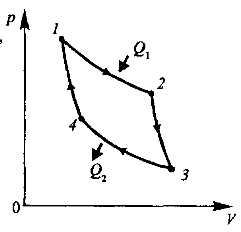
КПД
тепловой машины равен отношению
производимой работы А к количеству
теплоты
 полученному
рабочим телом от нагревателя:
полученному
рабочим телом от нагревателя:

Совершённая работа равна
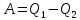
Где
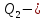 количество
теплоты, переданное холодильнику
количество
теплоты, переданное холодильнику
Поэтому
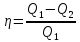
Полная работа равна сумме работ при изотермическом сжатии (процесс 1 – 2) и расширении (процесс 3 – 4):
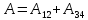
С
другой стороны

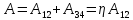
Поэтому
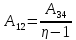
КПД цикла Карно
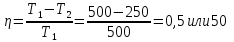
Тогда искомая работа
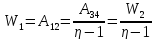
Работа
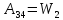 должна
быть отрицательной, т.к. тут происходит
изотермическое сжатие, а работа
должна
быть отрицательной, т.к. тут происходит
изотермическое сжатие, а работа
 положительной, т.к. тут происходит
изотермическое расширение.
положительной, т.к. тут происходит
изотермическое расширение.
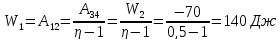
Ответ:
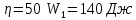
275. Какая энергия Е выделится при слиянии двух капель ртути диаметром d1 = 0,8 мм и d2 = 1,2 мм в одну каплю?
Решение. Коэффициент поверхностного натяжения жидкости равен
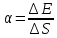
Где
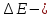 изменение
энергии при увеличении площади на
изменение
энергии при увеличении площади на

Для
ртути
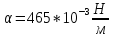
Искомая
энергия как раз и равна
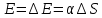
Объём
шара диаметром
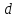 равен
равен
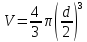
А его площадь
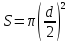
Начальная площадь ртути:

Полный объём ртути до и после слияния не изменился. Начальный объём равен объёму двух капель:

Конечный объём капли равен

А площадь
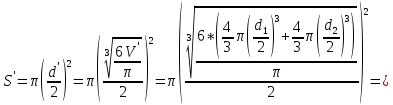
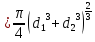
Тогда изменение площади равно
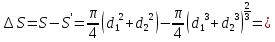
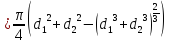
Тогда энергия слияния капель равна
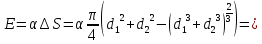
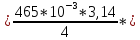
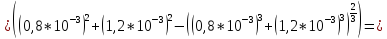
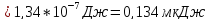
Ответ: