Амплитудный спектр, спектр мощности. Определение и алгоритмы получения.
Основу
спектрального анализа, как известно,
составляет преобразование Фурье. При
этом, для детерминированных периодических
сигналов
в большинстве случаев ограничиваются
амплитудным спектром:
(1.192)
где
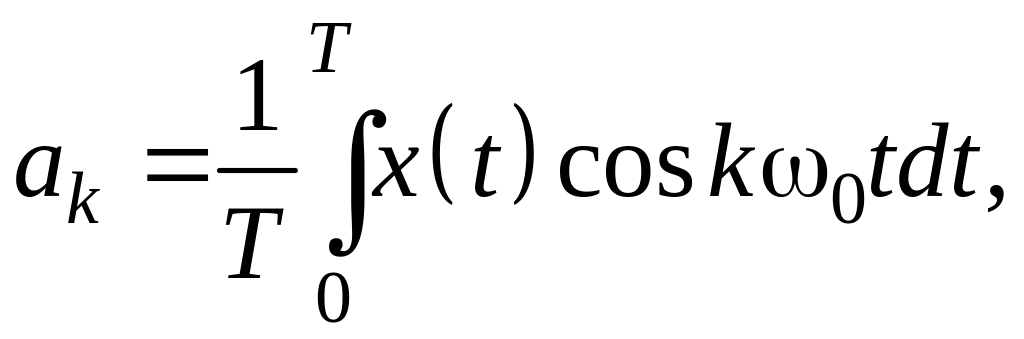
(1.193)
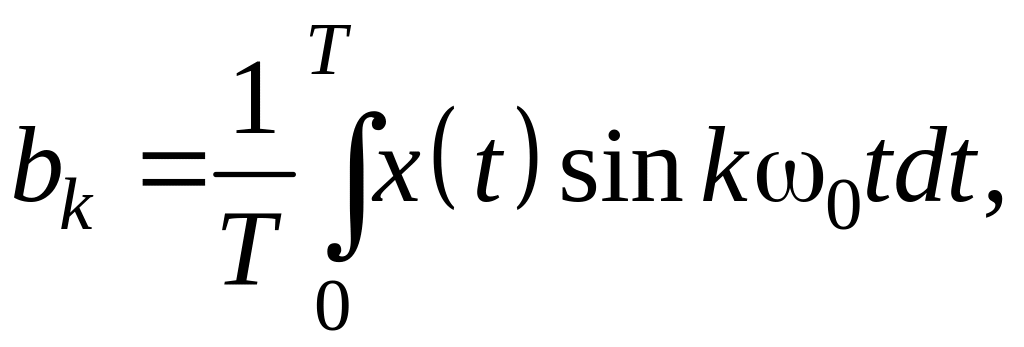
(1.194)
– коэффициенты соответствующего ряда Фурье.
Рассмотрим следующее определение спектральной плотности мощности, которое широко использовалось на практике до появления алгоритмов быстрого преобразования Фурье:
(1.199)
где x(t,,Δ) – процесс (сигнал) на выходе полосового фильтра с центральной частотой и полосой пропускания Δ.
Запишем данное выражение в более привычном виде:
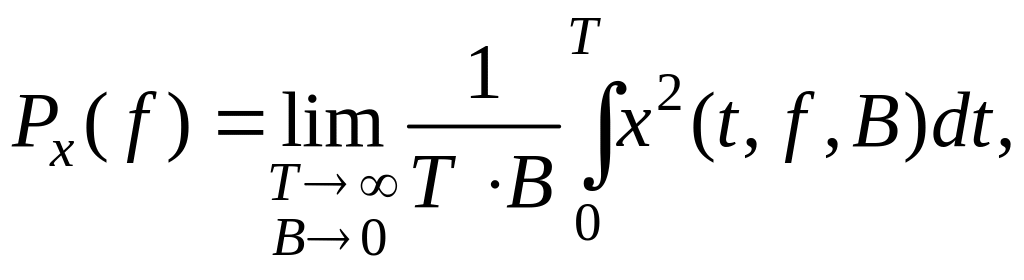(1.200)
где В – ширина полосы пропускания узкополосного фильтра с центральной частотой f.
Выясним
физический смысл выражения для
Как известно, если имеется временная
реализация некоторого сигнала х(t),
то
– это мгновенная мощность, а
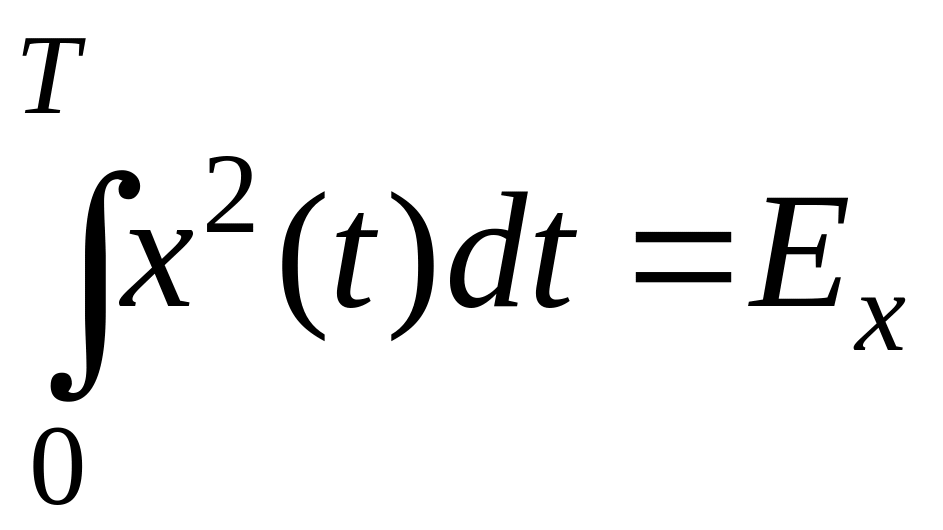(1.201)
– энергия, а величина
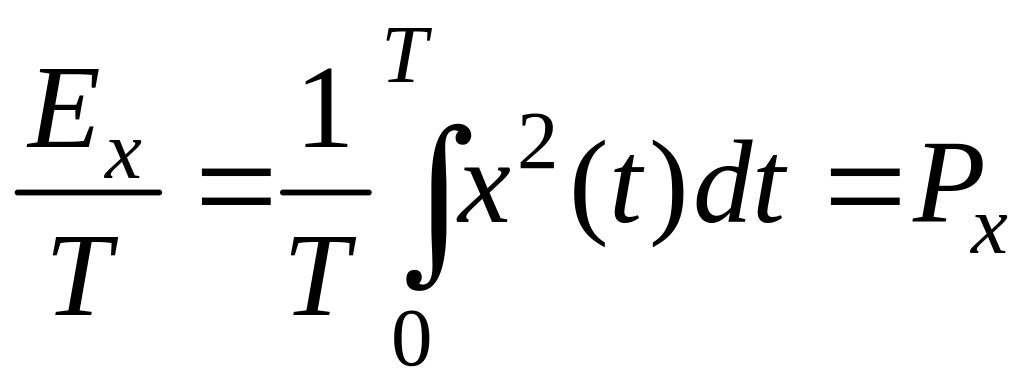(1.202)
является средней мощностью сигнала.
Тогда выражение
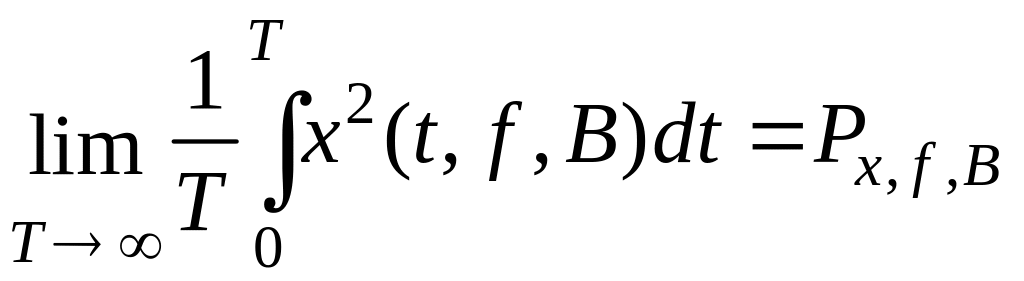(1.203)
определяет среднюю мощность сигнала на выходе полосового фильтра с центральной частотой f и полосой пропускания В.
Следовательно,
спектральная плотность мощности
– это мощность, приходящаяся на 1 Гц в
окрестности частоты f ,
т. е.
при В→ 0. (1.204)
Для получения оценки спектра мощности в некотором частотном диапазоне достаточно иметь или параллельный набор полосовых фильтров или же один полосовой фильтр с изменяемой центральной частотой. В первом случае получают спектр с постоянным относительным разрешением, во втором – с постоянным абсолютным разрешением.
Параллельный метод построения анализаторов спектра широко применяется и в настоящее время в спектральном анализе, звуковых измерениях и анализе шума.
Однако, в последнее время наиболее часто используется определение спектральной плотности мощности, основанное на непосредственном преобразовании Фурье исследуемой реализации:
(1.205)
где
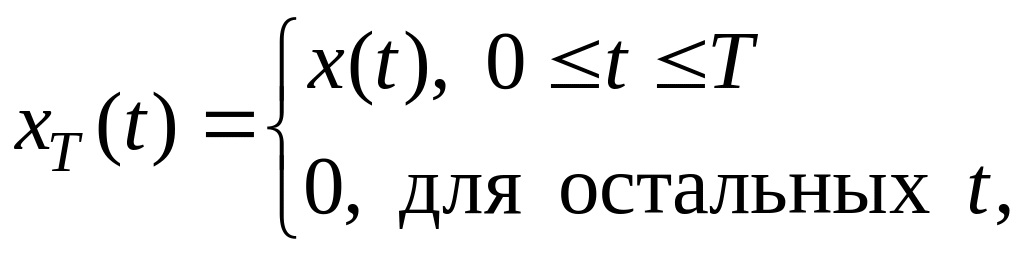
М – оператор статистического усреднения.
Оценка спектра мощности на основе периодограммы. Свойства периодограммы. Методы получения состоятельных периодограммных оценок.
В последнее время наиболее часто используется определение спектральной плотности мощности, основанное на непосредственном преобразовании Фурье исследуемой реализации:
(1.205)
где
М – оператор статистического усреднения.
Из данного определения оценка спектральной плотности мощности может быть получена в следующем виде
(1.206)
где
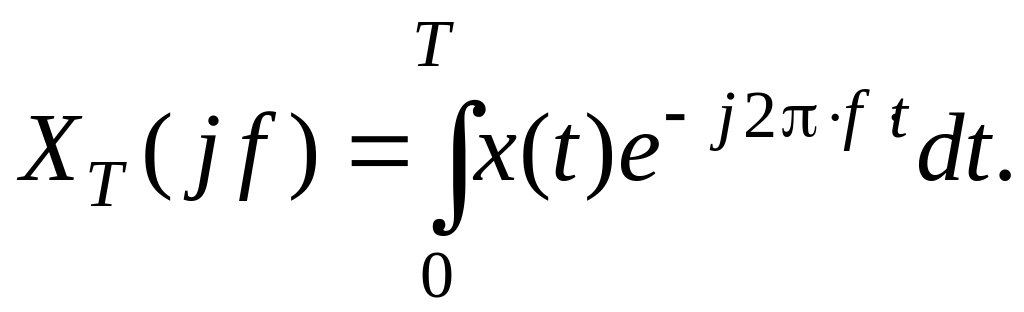
Здесь
– это односторонняя спектральная
плотность, поэтому в приведенном
выражении стоит цифра 2.
Основные свойства этой оценки:
(1.207)
т. е. данная оценка является асимптотически несмещенной.
Дисперсия данной величины
(1.208)
Это
значит, что асимптотически несмещенная
оценка
не является состоятельной. Другими
словами, средняя квадратическая
погрешность данной оценки равна 1 или
100 %.
Для
получения эффективных оценок применяются
методы сглаживания. В этом случае для
получения правильных результатов при
измерении
необходимо перейти от вычисления
точечной оценки к усреднению по множеству
таких оценок. На практике в связи с этим
возникают существенные трудности,
обусловленные тем, что усреднять по
множеству можно далеко не всегда. Как
правило, экспериментатор располагает
всего лишь одной или, в лучшем случае,
двумя-тремя реализациями исследуемого
процесса. Преодолеть возникшие трудности
можно воспользовавшись некоторыми
свойствами самой функции
часто называемой периодограммой.
Во-первых, она является случайной
функцией частоты. При этом интервал
корреляции по частоте составляет
величину, примерно равную
При
случайные величины
и
с увеличением интервала Т становятся
все менее коррелированными, т. е.
(1.209)
Это обстоятельство и лежит в основе получения состоятельных оценок спектральной плотности мощности, т. е. путем сглаживания (усреднения) оценки по сравнительно небольшому интервалу частот может быть получена оценка с убывающей дисперсией, хотя и с некоторым смещением (рис. 1.36).
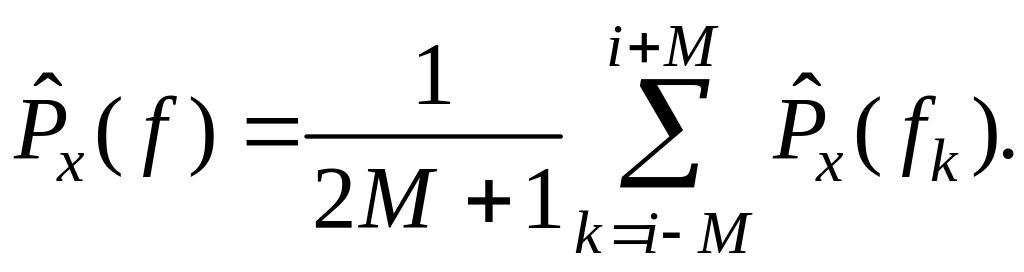(1.210)
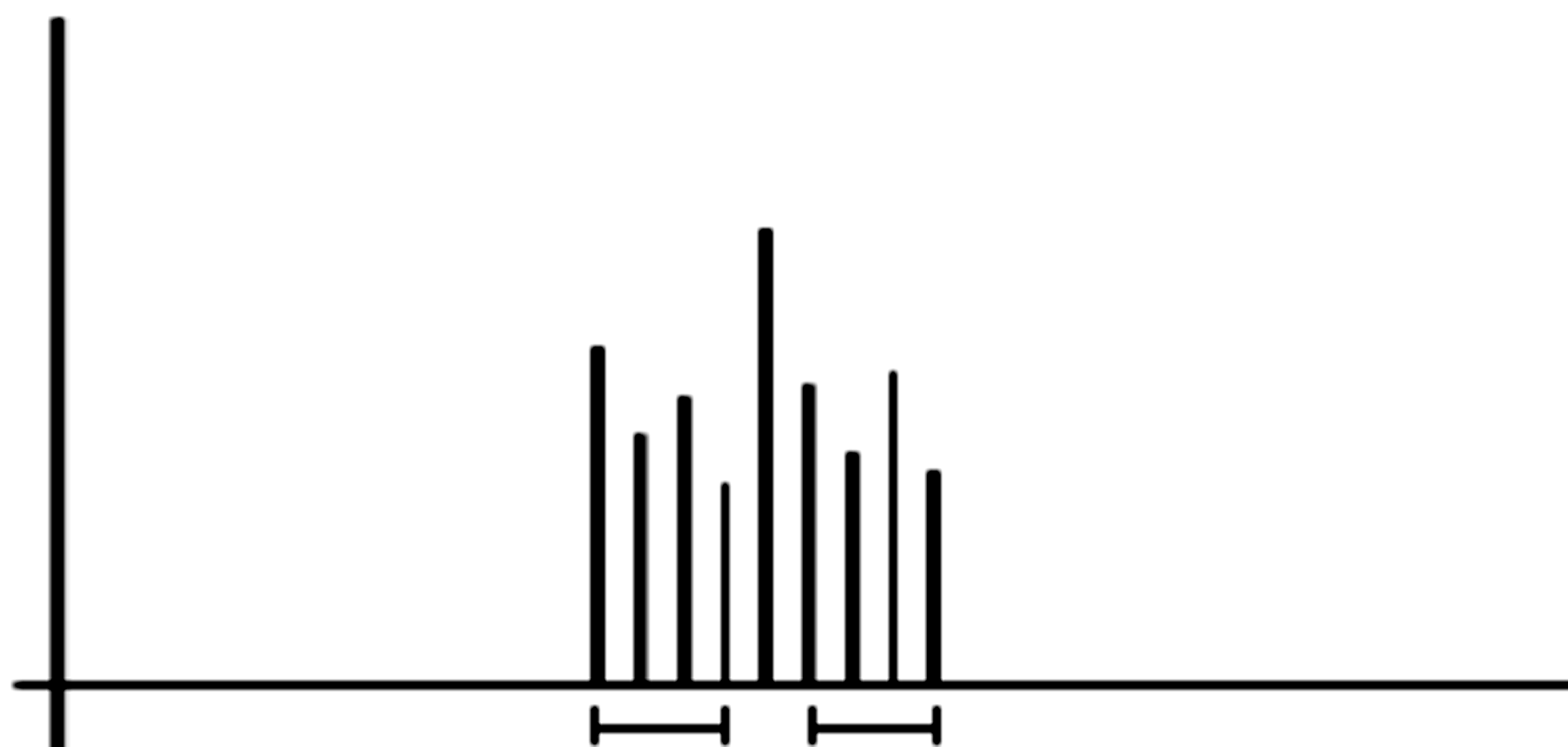
0 M f i M f
Рис. 1.36. Иллюстрация сглаживания по частоте
Для
этой же цели, кроме того, применяется и
усреднение по коротким периодограммам.
В этом случае исходная реализация
исследуемого сигнала x(t)
длительностью T делится
на более короткие реализации xi(t)
длительностью
По каждой реализации xi(t)
находится оценка
спектральной плотности, а затем
вычисляется их среднее арифметическое,
что позволяет уменьшить дисперсию
результирующей оценки в М раз (рис.
1.37).
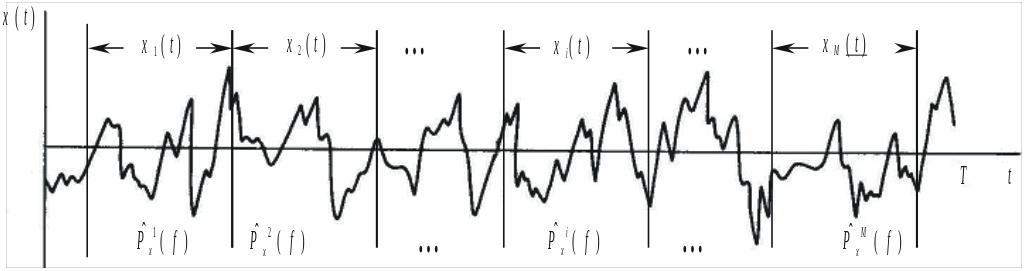
Рис. 1.37. Иллюстрация сглаживания по коротким реализациям
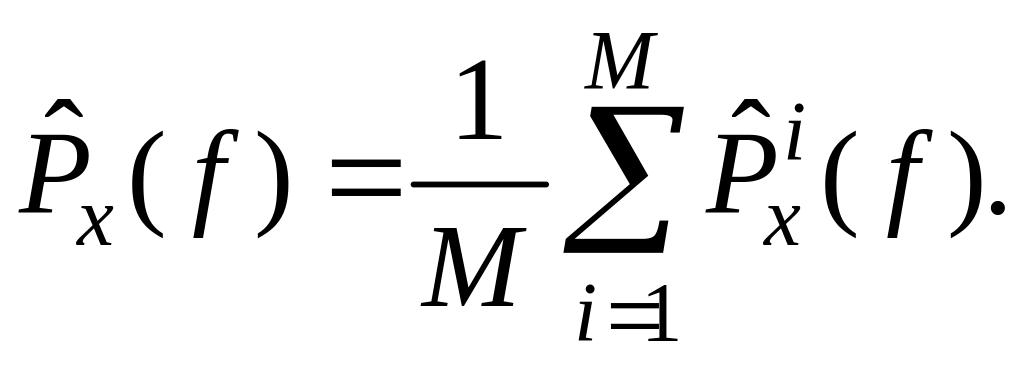(1.211)
Измерение (оценка) спектра мощности (часто называемого энергетическим спектром) дает возможность, например, получать информацию о динамических характеристиках линейных физических систем с постоянными параметрами, позволяет исследовать соотношения между процессами на входе и выходе таких систем, обнаруживать скрытые периодичности и т. д.
В теоретических исследованиях принято чаще всего говорить об оценке спектра или спектральном оценивании.
в настоящее время в спектральном анализе используются оценки спектральной плотности мощности, основанные на прямом преобразовании исходных данных и последующем их усреднении. Этот метод, как уже отмечалось, чаще называют методом периодограммной оценки спектра мощности.
Для того, чтобы по отсчетам обрабатываемого сигнала можно было бы получить спектральные оценки в соответствующих единицах энергии или мощности, необходимо выражение для прямого ДПФ умножить, а для обратного ДПФ разделить на интервал дискретизации t:
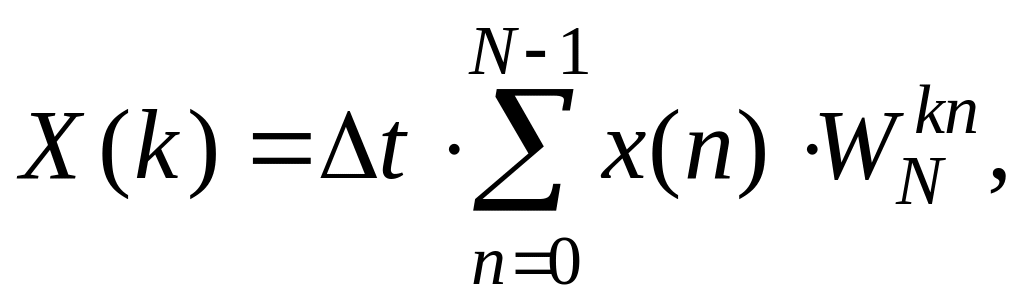
(1.212)
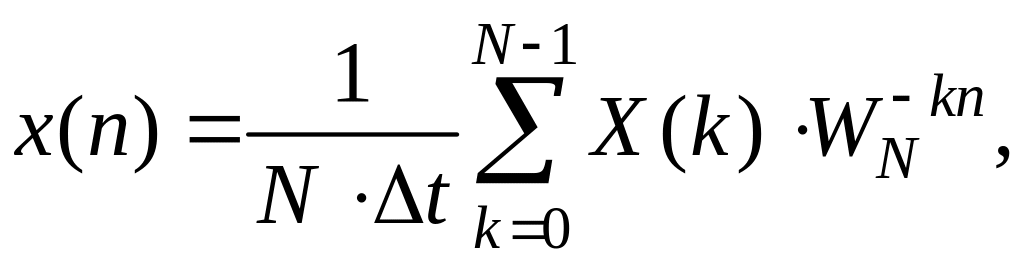
(1.213)
где
– интервал наблюдения (длительность
обрабатываемой реализации).
В этом случае оценка спектральной плотности мощности будет определяться следующим образом:
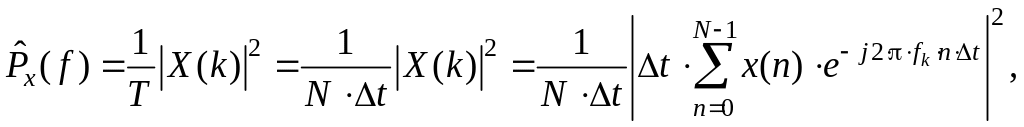(1.214)
где
Эта оценка называется выборочным спектром, периодограммой Шустера или просто периодограммой.
Данная оценка также не является состоятельной оценкой истинной спектральной плотности мощности (СПМ), так как дисперсия этой величины не стремится к нулю ни при каком сколь угодно большом значении N. Вследствие этого для получения состоятельных оценок требуется выполнение операции статистического усреднения. В этом случае будем иметь
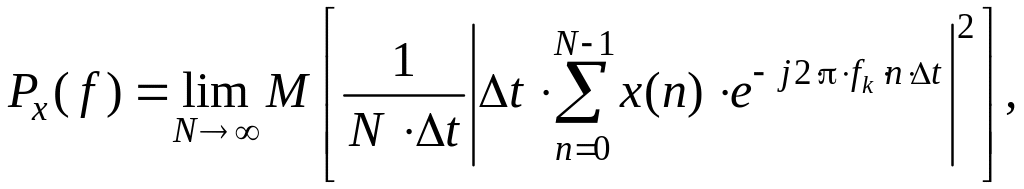(1.215)
Для расчетов используется выражение
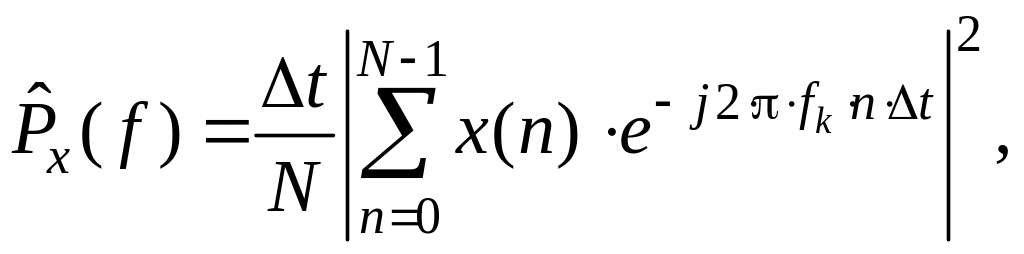(1.216)
которое называют исходной немодифицированной формой периодограммной оценки СПМ.
Для сглаживания периодограммной оценки используются три основных метода: метод Даньелла (Даниелла), Бартлетта и Уэлча. В методе Даньелла осуществляется усреднение оценок, полученных по соседним частотам (усреднение по смежным частотам), Бартлетта – по ансамблю (по коротким временным последовательностям), а в методе Уэлча подход Бартлетта применяется к перекрывающимся реализациям для уменьшения смещения оценок из-за эффекта просачивания.
Практическое использование этих трех процедур подтверждает их статистическую устойчивость для многих классов сигналов.
Периодограмма
Даньелла. Для сглаживания быстрых
флуктуаций выборочного спектра в этом
случае используется усреднение по
соседним спектральным частотам. Если
для вычисления выборочного спектра
на сетке частот
используется алгоритм БПФ, то сглаженная
оценка периодограммы на частоте
может быть получена посредством
усреднения М значений
с каждой стороны этой частоты:
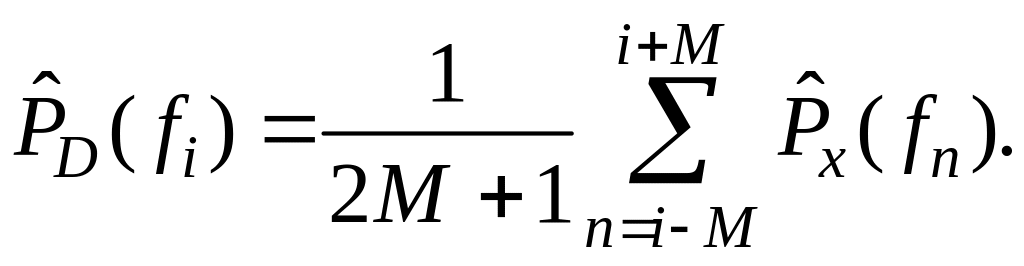(1.217)
Вычисление оценки по Даньеллу рекомендуется для случаев, когда анализируемое множество данных состоит из малого (100–500) или среднего (500–4000) числа выборок.
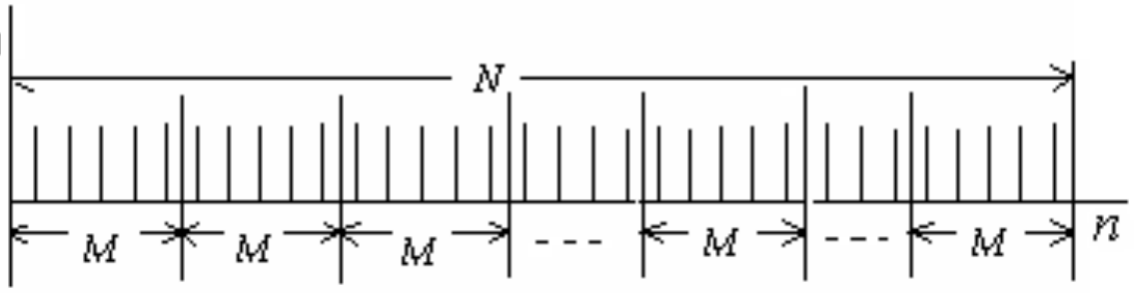
Периодограмма
Бартлетта. При этом подходе
последовательность входных данных х(п)
из N отсчетов делится на K
неперекрывающихся сегментов по М
отсчетов в каждом, так что
(рис. 1.38).
Тогда i-ый сегмент будет определяться таким образом:
(2.218)
Затем на каждом из этих сегментов независимо вычисляется выборочный спектр:
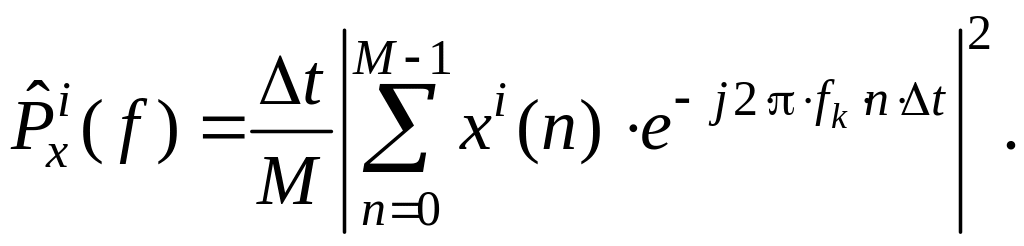(2.219)
Далее на каждой частоте, представляющей интерес, K отдельных немодифицированных периодограмм усредняются с тем, чтобы получить усредненную периодограмму Бартлетта.
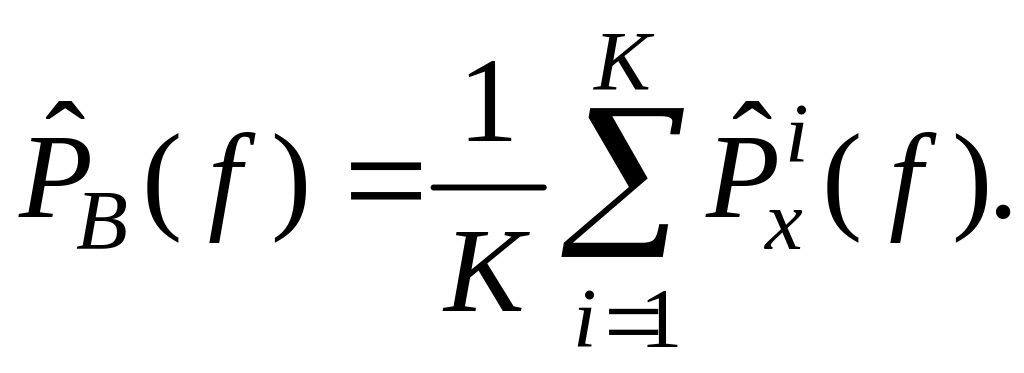(2.220)
x(n)
...
...
Рис. 1.38. К иллюстрации периодограммы Бартлетта
Дисперсия рассмотренной оценки уменьшается с увеличением числа K, а величина смещения – увеличивается, так как при фиксированной выборке N с увеличением числа сегментов число выборок М в каждом из них уменьшается. Это приводит к ухудшению разрешающей способности спектрального анализа, так что приходиться находить компромиссное решение между значениями N и М.
Данная оценка применяется при N > 2000.
Периодограмма Уэлча. Уэлч модифицировал основную схему Бартлетта за счет использования перекрывающихся сегментов (рис. 1.39). Цель перекрытия– увеличить число усредняемых оценок спектральной плотности мощности при заданной длительности исходной реализации и тем самым уменьшить дисперсию результирующей оценки.
На основе БПФ Уэлч разработал также эффективную вычислительную процедуру для реализации данного метода, что и сделало метод Уэлча самым популярным периодограммным методом спектрального оценивания.
Если
выборка из N отсчетов разбита на К
сегментов по М отсчетов в каждом со
сдвигом S отсчетов между соседними
сегментами
то максимальное число сегментов К
будет определяться целой частью числа
(N – M)/(S + 1).
Например, 50 %-е перекрытие сегментов во многих случаях обеспечивает весьма эффективную реализацию данного метода на основе алгоритмов БПФ. Кроме того, в этом случае все данные используются дважды, за исключением М/2 отсчетов на каждом конце исходной N-точечной последовательности данных. Следует отметить, что на практике часто используется перекрытие до 70 %.
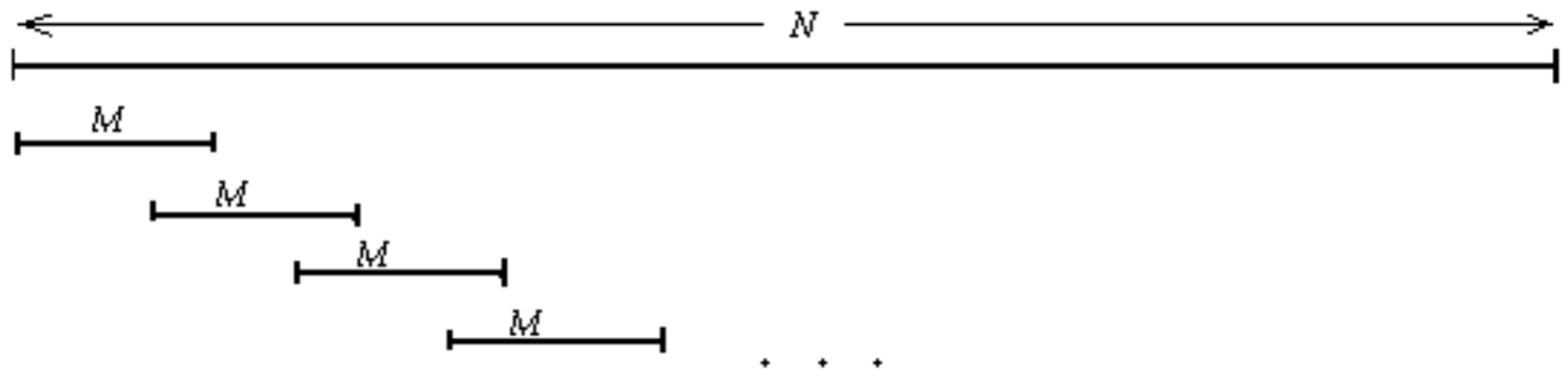
Рис. 1.39. Формирование периодограммы Уэлча
Также как и дисперсия периодограммы Бартлетта, дисперсия периодограммы Уэлча примерно обратно пропорциональна числу сегментов в предположении независимости сегментов (хотя перекрытие сегментов приводит к некоторой их взаимозависимости). Благодаря перекрытию по заданной выборке исходных данных можно сформировать большее число сегментов, чем в методе Бартлетта, что уменьшает величину дисперсии периодограммы Уэлча по сравнению с дисперсией периодограммы Бартлетта.