Вопрос 29. Эллипс.

Эллипсом называется множество всех точек плоскости, сумма расстояний которых до 2х данных точек называемыми фокусами, есть величина постоянная, большая чем расстояние между фокусами.

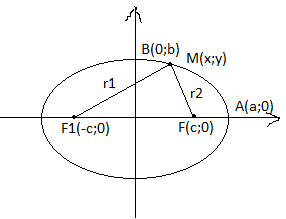
Обозначим F1 и F2-фокусы эллипса. Расстояние |F1F2|=C. Сумму расстояний от производной точки эллипса до фокусов обозначим через 2а .

По определению эллипса а>c, Для вывода уравнения эллипса введем параллельную систему координат к, чтобы фокусы эллипса лежали на оси абсцисс, а начало координат делило F1F2 пополам.

Пусть M(x;y)- произвольная точка плоскости. Обозначим расстояние r1=|F1M|, r2=|F2M|

Из определения эллипса следует, что точка M(x;y) будет лежать на эллипсе когда r1+r2=2a (1)

По формуле расстояние между 2мя точками мы можем переписать

=2a (3)

Урвнение (3)-есть ур-е эллипса. Но оно неудобно для использования.

Преобразуем :

Перенесем один радикал вправо и возведем обе части в квадрат.

Получим :

(x+c)² + y²=4a²-4a +(x-c)²+y²

Приводя подобные члены, получим:

a√((x-c)²+y²)=a²-cx (4)

Снова возведем обе части в квадрат

После упрощения получим:

(a²-c²)-x²+a²y²=a²(a²-c²) (5)

Обозначим ч/з b=√(a²-c²), тогда (5) ур-е примет вид: b²-x²+a²y²=a²b²

Разделив обе части на a²b², окончательно получим x²/a²+y²/b²=1 (6)

Любая точка координат которая удовлетворяет (6)-есть уравнение эллипса. Уравнение (6) называется каноническим уравнением эллипса.

Заметим, что (6) содержит только четные степени, поэтому эллипс симметричен относительно осей OX и OY и относительно начала координат. Т.о., чтобы знать формулу всего эллипса достаточно установить вид той части его, которая лежит в первом квадрате.

Для этой части y≥0 (6)=>

y= (7) Из (7) следует:

1.если x=0, то y=b, следовательно B(0;b) лежит на эллипсе

2. при возрастании числа x<a, b<y<0

3.если x=a => y=0 , следовательно точка A(a;0) лежит на эллипсе

4. когда x>a => a2-x2<0, следовательно x>a на эллипсе нет.

Итак, частью эллипса распол. В первой координатном угла является дуга BA. Проведя симметрию относительно начала координат и оси получим эллипс.

Если a=b, ур-е => x²+y²=a² (эллипс-окружность) . Оси симметрии наз-ся осями эллипса, а центр симметрии O –центром эллипса точки в которых эллипс пересек. оси-его вершина.

Величины a,b=большая и малая полуось эллипса. Эксцентриситетом эллипса называется отношение , где с-половина расстояний м/у фокусами, а-большая полуось эллипса. Т.к. с<а, то 0≤E≤1.

Принимая во внимание , что c²=a²-b²

E²= = = 1-( )² => =

И легко получится геометрическое истолкование эксцентриситета эллипса.

Т.о. эксцентриситет эллипса характеризует мру вытянутости эллипса. Как известно, планеты, нек. кометы движутся по эллипсическим траекториям. Оказывается, что эксцентриситеты планетарных орбит весьма малы, а кометы велики, то есть близки к 1.

Т.о., планеты движутся почти по окружности, а кометы приближаются к солнцу. Солнце находится в одном из фокусов, но значительно отдалено от него.

Вопрос 30. Гипербола.

Гиперболой называется множество всех точек плоскости, для которого модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная меньшая чем расстояние между фокусами, обознач. через F1 и F2, а расстояние между фокусами.

|F1F2|=2c, модуль разности расстояния от произвольной точки гиперболы до фокуса через 2а.

По определению 2a<2c или a<c .

Введем прямоугольную систему координат так, чтобы фокусы гиперболы лежали на оси абсцисс, а начало координат делило отрезок F1F2 пополам. Тогда фокусы гиперболы имеют координаты F1(-c;0), F2(c;0).

Выведем уравнение гиперболы. Пусть M(x;y) произвольная точка плоскости.

Числа |F1M|, |F2M| фокальными радиусами точки М и обозначается через r1,r2.

По определению |r1-r2|=2a (1) r1-r2= 2a

По формуле расстояния между двумя точками

(2)- уравнение гиперболы.

Преобразуем его. Перепишем один радикал вправо и возведем обе части в квадрат.

(c²-a²)x²-a²y²=a²(c²-a²) (3)

b²=c²-a² b²x²-a²y²=a²b²

(4)

Уравнение (4) называется каноническим уравнением гиперболы. Исследуем гиперболу по ее каноническому уравнению. Т.к. уравнение (4) содержит члены только с четными степенями ху, то гипербола симметрична относительно ху и относительно начала координат. Поэтому достаточно рассмотреть часть гиперболы, лежащей в первом координатном угле. На этой части y ≥0. Поэтому разрешая (4) уравнение относительно (у), получим

(5)

Из (5) следует:

1.Если 0≤x≤a , то x²-a²<0, следовательно, точки гиперболы с такими координатами нет.

2.Если x=a, то y=0, следовательно точка A(a;0) лежит на гиперболе.

3.Если x>a, то y>0, причем y возрастает с возрастанием x и y стремится к ∞ , при x стремящегося к ∞.

Переменная точка M(x;y) на гиперболе движется с ростом x вправо и вверх, а ее начальное положение A(a;0), причем точка M(x;y), уходя по гиперболе в ∞, неограниченно приближается к прямой

(6) называемой асимптотой гиперболы.

Вид гиперболы легко установить, используя симметрию относительно координатных осей. Гипербола имеет вид ветви и две асимптоты.

Оси симметрии называются осями гиперболы, а центр симметрии О-центром гиперболы . Точки А и А^{l –}вершины гиперболы. Прямоугольник BB^lC^lC со сторонами 2a и 2b называется основным прямоугольником гиперболы.

Величина a,b наз-ся действительной и мнимой полуосями гиперболы:

также определяет гиперболу.

Она изображена пунктиром. Вершина ее лежит на оси ОУ. Эта гипербола называется сопряженной по отношению к гиперболе (4)

Гипербола с одинаковыми полуосями называется равносторонней, и ее каноническое уравнение имеет вид x²-y²=a².

Асимптоты равносторонней гиперболы взаимно перпендикулярны.

Эксцентриситетом гиперболы называется решение . Чем меньше эксцентриситет, тем больше прямоугольник вытянут в направлении действительной оси.