-
Подбор аппроксимирующей функции
После того как установлен графических вид искомой функциональной зависимости, задача состоит в выборе ее аналитического описания, т.е. в подборе аппроксимирующей функции.
Известно, что любую функцию для
однофакторных совместных измерений
можно описать многочленом
,
она же линейная регрессия. В простейшем
случае может использоваться модель
вида
.
В случае линейной регрессии для
определения параметров модели используется
метод наименьших квадратов.
Также очень удобными при аппроксимации оказываются дробно-рациональные функции. Их практическая особенность в том, что чаще всего исследователь не подозревает, что интересующая его зависимость аппроксимируется именно этими функциями. Целесообразно взять себе за правило, прежде чем использовать аппроксимацию многочленом или экспонентами, обязательно проверить, не является ли искомая кривая простейшей, сдвинутой от начала координат гиперболой.
Рисунок 3
Рисунок 4
Проверка того, является ли данная кривая
гиперболой, состоит в построении графика
(рис 4). Если является, то экспериментальные
точки примерно (из-за наличия погрешностей)
ложатся на прямую.
При этом замена координаты y
на
допустима лишь в том случае, если сдвиг
по этой координате отсутствует, т.е.
другая ось является асимптотой такой
гиперболы. Это вызвано тем, что при
сдвиге, например, вдоль оси x
аналитическое описание гиперболы имеет
вид
.
Обращение оси y приводит
к зависимости вида
,
т.е. прямой в координатах
.
При сдвиге же вдоль оси y
уравнение гиперболы имеет вид
,
а следовательно,
не есть прямая линия.
Для того чтобы использовать МНК для
дробно-рациональной модели необходимо
произвести замену
,
если это возможно, и оценивать параметры
упрощенной модели.
-
Расчет по экспериментальным данным параметров выбранной аппроксимирующей функции
Подставив полученные из опыта числовые
значения
и
,
в выбранную для аппроксимации функцию,
получим ряд уравнений.
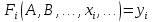(1)
Как уже отмечалось, обычно число уравнений системы (1) превышает число неизвестных и из-за погрешностей измерений нельзя найти такие значения измеряемых величин, чтобы одновременно удовлетворились все уравнения, даже если они сами по себе точно известны. Поэтому уравнения (1) в отличие от обычных математических уравнений принято называть условными. При подстановке в условные уравнения (1) найденных каким-то путем значений неизвестных по отмеченным причинам получим
Величины
принято называть невязками. Всеобщее
признание получило такое решение
условных уравнений, которое приводит
к минимуму сумму квадратов невязок, что
осуществляется методом наименьших
квадратов. Теоретически показано, что
при нормальном распределении погрешностей
метод наименьших квадратов приводит к
оценкам неизвестных, удовлетворяющих
принципу максимума правдоподобия, т.е.
наиболее вероятным оценкам.
Пусть система условных уравнений имеет вид
,
(2)
причем A
и B - искомые неизвестные,
и
- результаты i-го наблюдения
величин x и y.
Если в (2) подставить какие-то оценки
величин
и
,
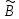то получим невязки:
.
Найдем оценки величин
и
исходя из следующий условий МНК:
SSE - сумма квадратов невязок.
Для выполнения этого условия необходимо, чтобы
Найдем эти частные производные и приравняем их нулю:
Отсюда получаем систему так называемых нормальных уравнений:
При написании нормальных уравнений часто пользуются обозначениями Гаусса:
и т.д.
В обозначениях Гаусса нормальные уравнения принимают более простой вид:
(3)
Нужно обратить внимание на две важные особенности матрицы коэффициентов при неизвестных в системе уравнений (3):
1. Матрица этих коэффициентов симметрична относительно главной диагонали.
2. Все элементы главной диагонали положительны.
Эти свойства являются общими, они не зависят от числа неизвестных, но в данном примере показаны применительно к случаю с двумя неизвестными.
Число нормальных уравнений равно числу неизвестных, и их решение известными методами дает интересующие нас оценки измеряемых величин. Наиболее кратко решение записывается с помощью определителей:
,
(4)
где
.
Определители
и
получают из главного определителя
системы D путем замены
столбца с коэффициентами при неизвестных
и
на столбец со свободными членами:
,
.
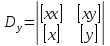Теперь нужно оценить погрешности полученных результатов. В упрощенном виде оценки дисперсий найденных значений неизвестных можно вычислить, пользуясь формулами:
где
и
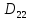- алгебраические дополнения элементов
и
определителя
D соответственно (они
получаются путем удаления из матрицы
определителя D столбца и
строчки, на пересечении которых находится
данный элемент).
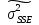- оценка дисперсии условных уравнений.
Оценка дисперсии условных уравнений вычисляется по формуле:
Метод наименьших квадратов дает возможность найти оценки измеряемых величин и оценить их среднеквадратические отклонения.
Доверительные интервалы для истинных
значений измеряемых величин строят на
основе распределения Стьюдента. Число
степеней свободы в общем случае равно
.
В нашем случае m = 2 - число
оцениваемых параметров.