
- •Тема: Физико-математические модели климатических изменений Лекция 12. Классификация моделей. Энергобалансовые модели.
- •Структура
- •Иерархия климатических моделей
- •Иерархия современных климатических моделей (Катцов, Мелешко, 2004)
- •Тепловой баланс системы Земля - атмосфера
- •1. Энергобалансовые модели (ЭБМ)
- •Осредненный по широтным зонам термический режим
- •Определение параметров модели
- •2). Длинноволновое излучение I*
- •Модель для сезонов (Будыко, Васищева, 1971)
- •Средние широтные температуры (северное полушарие)
- •Средние планетарные температуры
- •Чувствительность модели
- •Приложение модели
- •1.2. Одномерная модель Селлерса (1969)
- •Схема переменных, параметров и взаимодействий в термодинамической модели континентальных областей
- •Схема переменных, параметров и взаимодействий в термодинамической модели океанических областей
- •1.3. Нульмерная модель ледниковых периодов В.Я.Сергин и С.Я.Сергин
- •1.4. Нестационарная модель энергетического баланса Земли
- •Модель
- •1.5. Двумерные модели энергетического баланса
- •1.5. Двумерные модели энергетического баланса
Тема: Физико-математические модели климатических изменений Лекция 12. Классификация моделей. Энергобалансовые модели.
1.Физическое моделирование климата в лабораторных условиях невозможно: горизонтальный масштаб - это окружность Земли =
107 м, вертикальный - 104 м , соотношение масштабов 10-2-10-3.
2.Активный эксперимент с климатической системой невозможен.
3.Эмпирико-статистические модели могут дать описание динамики и установить закономерности, но не могут: -оценить какой вклад вносит каждый фактор в изменение
климата; -восстановить климаты прошлого;
- дать прогноз изменений климата.
4. Физико-математические модели
Однако проблемы:
-отсутствие данных о состоянии системы (всего 40 лет, 700 станций, на океанах очень мало);
-климатическая система – тонкая пленка, третье измерение очень мало и распределение энергии по спектру двухмерной жидкости принципиально отличается от распределения в 3х-мерной (теория турбулентности Колмогорова: передача и рассеивание энергии от крупного масштаба к мелкому), надо уметь считать энергию, генерируемую в мелких масштабах.
Создание моделей, всё более и более подробно и точно описывающих физические процессы, участвующие в формировании климата, в явном виде, в перспективе - все, от подвижки геологических плит до каждого облака и даже до червей, меняющих пористость почвы.
Структура |
Химический макроблок |
Биологический макроблок |
|
(циклы: углерода, кислорода, хлора, брома, |
(климатообразующие процессы, |
|
фтора, водорода в атмосфере и океане, |
сформированные деятельность живых |
|
озона – в стратосфере) |
организмов на суше и в океане) |
|
Термодинамический макроблок |
Классификация моделей климата |
(законы сохранения импульса, энергии, |
массы, воды в атмосфере, океане, на суше) |
1. Энергобалансовые модели (ЭБМ):
- одномерные (зависимость от широты),
- двумерные (широта и долгота), - нестационарные (изменение температуры во времени в зависимости от изменения факторов),
- резервуарные (боксовые) с выделением подсистем или географических и функциональных
признаков (атмосфера, глубокий океан, криосфера, атмосфера тропиков, суша полушария).
2. Радиационно-конвективные модели (РКМ):
- основное назначение – моделирование вертикальной термической структуры атмосферы за счет радиационного теплообмена, конвекции и теплового взаимодействия с поверхностью.
3. Динамико-стохастические модели:
- двумерные (широта и высота) модели атмосферы.
4. Модели промежуточной сложности (МПС):
- для решения задач, которые не могут быть решены на полных моделях (моделирование палеоклимата климата, изучение особенностей подстилающей поверхности).
5. Модели общей циркуляции атмосферы (МОЦА):
- глобальные трехмерные модели, основанные на полных уравнениях термогидродинамики.
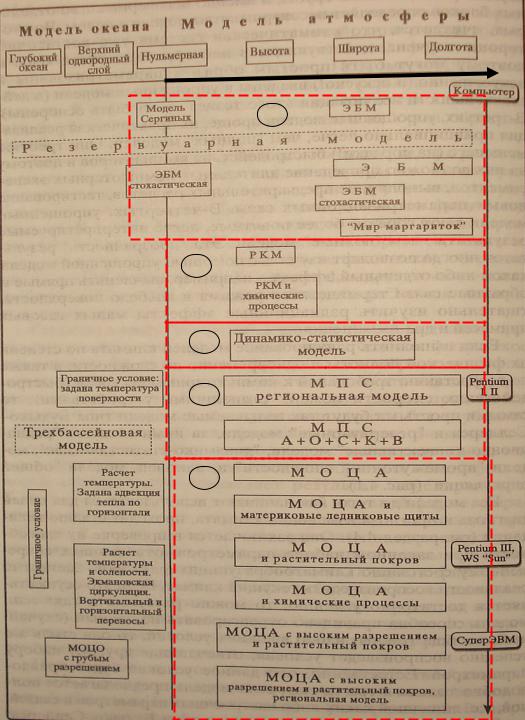
Иерархия климатических моделей
ЭБМ – энергобалансовая модель.
РКМ - радиационно-конвективная модель. МПС – модель промежуточной сложности. А+О+С+К+В – атмосфера, океан, суша, криосфера.
МОЦА – модели общей циркуляции атмосферы. МОЦО – модели общей циркуляции океана.
МОЦА:
-грубое разрешение (500Х500 или 500Х700 км, до 10 уровней по вертикали);
-среднее разрешение (200Х200 км, 20 уровней по вертикали);
-высокое разрешение (30Х30 км).
Направления развития:
-кардинальный переход к более совершенным моделям; -совершенствование других блоков
климатической системы (океан, суша, перенос химических соединений);
-вложение региональных моделей (РМ) в МОЦА: МОЦА/МОЦО, МОЦА/РМ для оценки чувствительности, исследования автоколебаний системы при неизменных внешних параметрах, прогноз при нестационарных численных экспериментах.
1
2
3
4
5
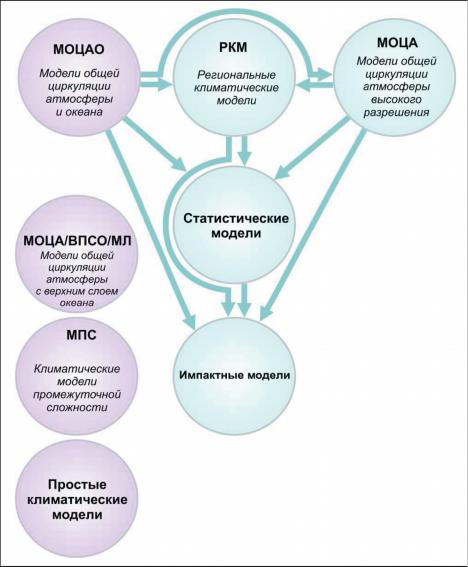
Иерархия современных климатических моделей (Катцов, Мелешко, 2004)
1) простые климатические модели (двумерные, одномерные или даже нульмерные);
2) модели промежуточной сложности (МПС - Integrated Assessment Models);
3) модели общей циркуляции атмосферы (МОЦА) с упрощенными описаниями верхнего перемешанного слоя океана и морского льда (ВПСО/МЛ); 4) сложные трехмерные модели совместной циркуляции
атмосферы и океана (МОЦАО), занимающие высшую ступень в иерархии климатических моделей.
Простые модели используются для оценки влияния на климат сокращения выбросов ПГ в атмосферу либо как компоненты так называемых моделей совокупной оценки (например, для анализа стоимости таких сокращений).
МПС не столько уступают МОЦАО в количестве описываемых процессов, сколько в детальности, сложности этих описаний.
МПС, так же как и МОЦА/ВПСО/МЛ, полезны в исследованиях отдельных физических процессов, их взаимодействий и обратных связей между ними, а также применяются в исследованиях палеоклимата.
Основным преимуществом моделей, находящихся на более низких ступенях иерархии, является их вычислительная эффективность, позволяющая проводить с простыми моделями и МПС массовые ансамблевые расчеты, а также интегрировать их на сравнительно долгие (тысячи лет) сроки. Продолжительность экспериментов с МОЦА/ВПСО/МЛ в исследованиях равновесных состояний климатической системы обычно не превышает нескольких десятилетий модельного времени.
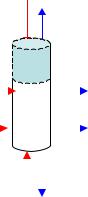
Тепловой баланс системы Земля - атмосфера
Притоки тепла
1). Поглощение солнечной энергии Qs(1-αs);
2). Конденсация водяного пара с выделением тепла LC (C- масса водяного пара сконденсировавшаяся в единицу времени над ед. площадью);
3).Перенос тепла горизонтальными атмосферными течениями Q1; 4). Перенос тепла горизонтальными океаническими течениями F1.
Стоки тепла
1). Испускание в космос теплового инфракрасного излучения I*s;
2). Испарение воды с расходом тепла LE;
3). Вынос тепла горизонтальными атмосферными течениями Q2; 4). Вынос тепла горизонтальными океаническими течениями F2.
Qs(1-αs) |
Изменение теплосодержания внутри колонны воздуха Ts: |
I*s |
Ts=Qs(1-αs)+LС+Q1+F1-I*s-LE-Q2-F2
Q1 |
|
|
|
|
|
|
Q2 |
|
|
|
|
|
|
Ts |
R =Q (1-α )-I* |
|
радиационный баланс Земля - атмосфера |
||||||
F |
1 |
|
|
|
|
|
|
F2 |
s s s |
s |
|
|
|
|
|
|
|
|
|
|
R =LΔC+ΔQ+ΔF |
тепловой баланс (баланс энергии) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
LC |
LE |
|
s |
|
системы Земля - атмосфера |
||
LΔC=L(E-C) – поток скрытого тепла, ΔQ=Q2-Q1, ΔF=F2-F1 - потоки явного тепла и Ts=0 за год.
1. Энергобалансовые модели (ЭБМ)
Любая климатическая модель в основе которой лежит уравнение сохранения энергии. Исторически – простые модели типа Будыко-Селлерса (Будыко, 1968; Sellers, 1969).
1.1. Одномерная модель М.И.Будыко
S/4 (1 - α)= I*, I*= ε σT4 I*= A+BTs A= a1-na2 B= b1-nb2 или I*= a1+b1Ts-(a2+b2Ts)n
S/4 = 340Вт/м2 - средний поток энергии Солнца, приходящий на единицу площади поверхности сферы при потоке S через площадь ее поперечного сечения;
S - αS = S (1 - α) – поглощенная земной поверхностью радиация, α –альбедо (0.30 для Земли);
I* - эффективное излучение;
Тs – температура земной поверхности в абс. шкале;
σ=5.670*10-8 Вт/(м2К4) постоянная Стефана-Больцмана; ε - относительный коэффициент излучения = 0.95;
A, B – эмпирические коэффициенты, А=203Вт/м2, В=2.09Вт/(м2 0С) при n=0.5; 0<n<1 –балл эффективной облачности.
Автор |
а1 |
а2 |
|
b1 |
b2 |
B |
|
|
Вт/м2 |
|
|
Вт/(м2 К) |
при n=0.5 |
|
|
|
|
|
||
Будыко (1968), Атлас теплового баланса |
222.5 |
47.4 |
2.23 |
1.60 |
1.43 |
|
Сесс (1976), спутниковые данные для I* |
257 |
91 |
1.63 |
0.11 |
1.57 |
|
Раманатан (1976), модельные расчеты |
227 |
45.1 |
2.16 |
1.75 |
1.28 |
|
Мохов и Петухов (1978), теоретическое обоснование |
231 |
59 |
2.40 |
0.65 |
2.07 |
|
При линеаризации ΔI*= 4ε σT3ΔT |
и T=288К=150С |
I*= 4ε σT3= B=5.15 Вт/(м2*К) |
||||
При подстановке А и В по Мохову в |
S/4 (1 - α)= А+ВТs |
Тs =150С Т =14.90С сев. пол. |
||||
Осредненный по широтным зонам термический режим
Эмпирический вывод: приток тепла, обусловленный переносом его по горизонтали, пропорционален разности между температурой на фиксированной широте (Тφ) и средней
планетарной температурой (Тs):
I0 (1 - α)- I*=β(Tφ-Ts) ,
I0 = 1.37 кВт/м2 – солнечная постоянная, β- коэффициент пропорциональности.
Учитывая, что: TS |
1 |
[I0 (1 ) a1 |
a2 n] и I*= a +b T |
|
-(a +b T )n |
|
φ |
||||
|
b1 b2 n |
|
1 1 |
2 2 φ |
|
|
|
|
|
|
T |
I0 (1 ) a1 a2 n TS |
|
I0 (1 ) A TS |
или |
|
|
|
||||
|
b1 |
b2 n |
|
B |
|
|
|
|
|||
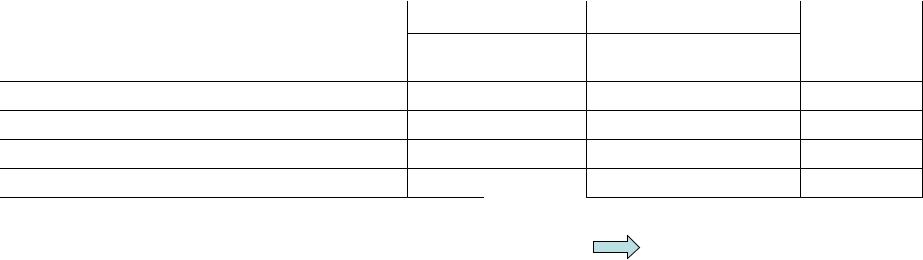
Меридиональные распределения радиационно- равновесной температуры:
(1)– при отсутствии межширотного переноса энергии (S=(1-α)/4=A+BTs при Ts=14.90С);
(2)– при фактическом переносе;
(3)– при бесконечно интенсивном переносе – мгновенное выравнивание межширотного
различия в количестве поглощенной радиации =14.90.
S(φ)[1 - α(φ)] - I*(φ) = Rs(φ)=div F
Rs(φ) – разность между поглощенным излучением Солнца и реальным уходящим
тепловым излучением в широтной зоне (радиационный баланс);  x=sinφ F(φ) –межширотный поток тепла, переносимый атмосферой и океаном.
x=sinφ F(φ) –межширотный поток тепла, переносимый атмосферой и океаном.
Определение параметров модели |
S(φ)[1 - α(φ)] - I*(φ) = Rs(φ)=div F |
1). Альбедо системы Земля-атмосфера зависит от угла падения солнечных лучей, уменьшаясь при возрастании этого угла.
α=αсс+αs(1-c) |
αs- альбедо Земли при безоблачной атмосфере, αc- альбедо облачного покрова, |
|
с- доля земной поверхности, покрытая облачностью. |
||
|
В модели 1968 г. α=0.32 и α=0.62 для суши и льдов.
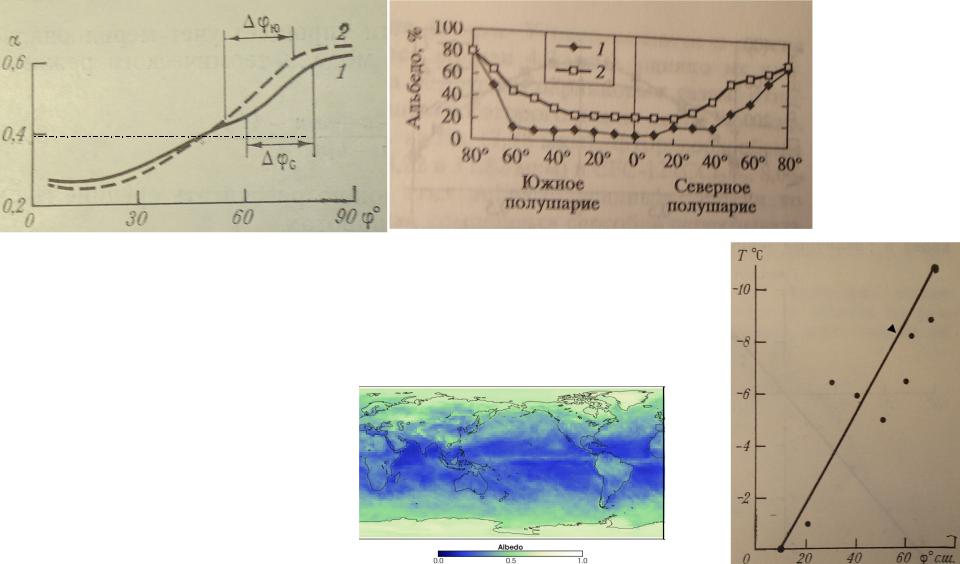
Зависимость α от широты по данным Эллиса и Вондер Хаарома (1976), где 1- северное, 2 – южное полушарие, Δφ – области перехода от безледной зоны к зоне со сплошным ледяным покровом.
При расчетах широтного распределения α необходимо учитывать положение средней границы постоянного ледяного покрова. Полагая, что снежный покров устанавливается при Тс можно
параметризовать α=f(T)
α = α при T(x)≤T |
с |
Альбедная |
|
|
I |
|
обратная |
|
|
= αL |
при T(x)>Tс |
связь |
|
|
αI - альбедо, когда облачность |
|
|
||
отсутствует, а поверхность покрыта |
|
|||
снегом (льдом); |
|
|
март 2005 г. |
|
αL - альбедо при бесснежных условиях. |
||||
Зависимость температуры на границе снежно- ледяного покрова от широты
Зонально- осредненные средние за год значения альбедо подстилающей поверхности (1) и планетарного альбедо (вместе с атмосферой) (2) как функция широты.
снеговая (снежная) линия 
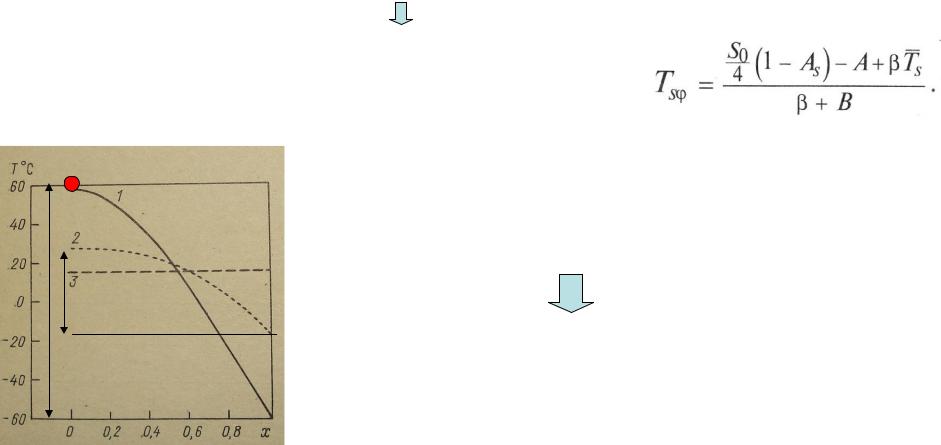
2). Длинноволновое излучение I*
I*= a1+b1Ts-(a2+b2Ts)n
Теоретическая формула Манабе и Везеролда (1967)
I*=14+0.14T -1.6n
1). Материалы спутниковых наблюдений (Cess, 1976)
2). Расчет по уточненным данным облачности (И.М.Беева.К.Я.Винников)
I*=16.2+0.106T -4.75n
Результат
ср=1.20С
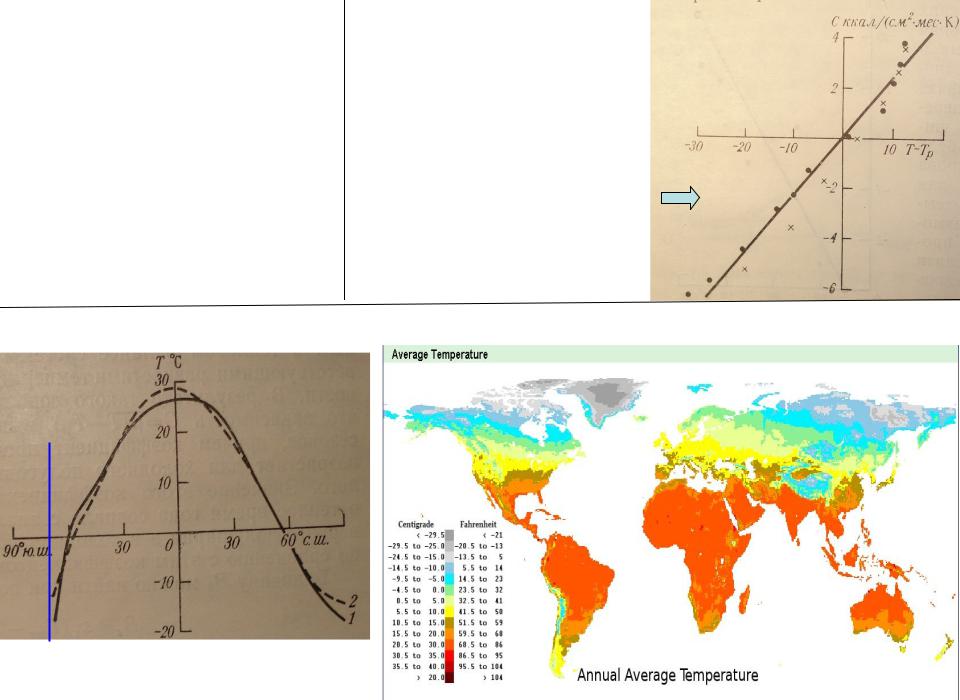
3). Коэффициент пропорциональности β
С – меридиональное перераспределение тепла (равно радиационному балансу системы Земля – атмосфера для средних годовых условий).
Зависимость меридионального распреде- ления тепла от разности среднеширотной и планетарной температур.
β=0.232 ккал(см2 *год *0С)
Распределение средней широтной температуры (без Антарктиды)
1 – расчет, 2 – эмпирические данные.
Модель для сезонов (Будыко, Васищева, 1971)
QST (1 - αST) - I*ST=CT+BS |
BS –приход или расход тепла из-за охлаждения или нагревания |
|
системы Земля – атмосфера (в основном процесс охлаждения или |
||
|
||
QSХ (1 - αSХ) - I*SХ=CХ+BS |
нагревания океана); |
|
С – сумма потоков тепла, обусловленная горизонтальными |
||
Расчет составляющих: |
движениями в атмосфере и гидросфере. |
|
I*= a1+b1Ts-(a2+b2Ts)n |
|
|
Q (1 - α)- I*=β(Tφ-Ts)=C , |
β – коэффициент пропорциональности несколько возрастает для |
|
холодного и уменьшается для теплого полугодий. |
||
BS=sγ(TWT-TWХ) |
|
s –отношение площади океанов в данной широтной зоне к общей площади широтной зоны; TWT, TWX –средняя широтная температура поверхности океана в теплый и холодный сезоны;
γ – коэффициент размерности.
Уравнение теплового баланса океанов (для определения TW):
RWT=LET+PT+BS/s,
RWХ=LEХ+PХ-BS/s+F0,
RW – радиационный баланс поверхности океанов;
LE – затрата тепла на испарение;
Р – турбулентный поток тепла между океаном и атмосферой; F - перенос тепла течениями (зимой).
Приближенные соотношения для определения LE, P, F0:
F0=β’(TХ-Ts) LE = fTW, P=c (TW – T ),
ТW – температура поверхности океана в 0С,
ТХ – температура воздуха холодного полугодия
γ=3.0, f=0.4, βТ =0.2, βХ=0.27, β’=0.14 для северного полушария, βХ=0.40, β’=0.20 – для южного полушария, с=0.84.
