- •Лекция 14. Модели общей циркуляции атмосферы и океана
- •МОЦАО – должна правильно описывать отклик на малые внешние возмущения, т.к. используется для
- •Основные уравнения составляющих (блоков) климатической системы
- •Уравнения переноса радиации
- •Уравнения переноса влаги и примесей
- •Б. Уравнения блока океана
- •Г. Снежный покров и морские льды
- •Д. Материковые льды
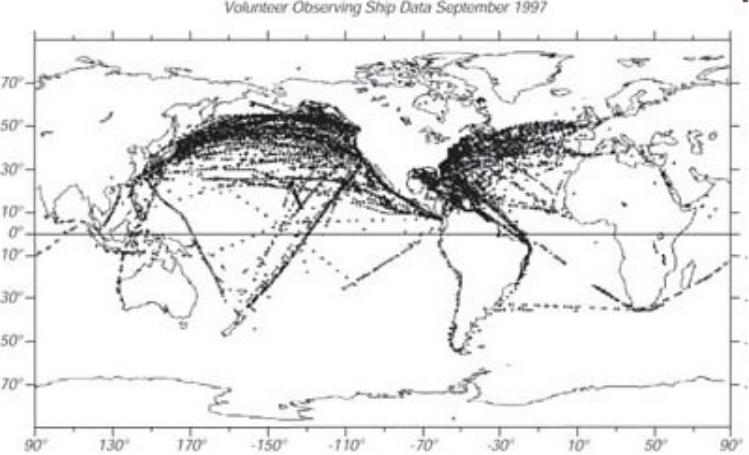
- •Трассы судов, ведущих гидрометеорологические наблюдения в океанах
- •Международная программа AMIP (Atmospheric Model Intercomparison Project).
- •Атмосферная модель (HadAM3)
- •Чувствительность климата к удвоению содержания СО2 для моделей МГЭИК-4
- •Coupled Model Intercomparison Project - CMIP3, CMIP5
- •Название и назначение численных экспериментов проекта CMIP5
- •В проекте CMIP5 вместо применяемых ранее сценариев SRES (В1, А1В, А2, соответствующих концентрации
- •Модели CMIP5
- •Основные свойства моделей общей циркуляции атмосферы и океана (МОЦАО или AOGCM) и моделей
- •5.1. Модель ИВМ РАН Дымников, Лыкосов, Алексеев, Володин (1998)
- •В качестве краевых условий для системы уравнений предполагается периодичность решения по долготе, а
- •Подсеточные процессы
- •Воспроизведение современного климата 1. Моделирование общей циркуляции атмосферы при заданных пространственно-временных распределениях
- •Давление в июне - августе
- •Температура воздуха у поверхности в декабре – феврале (1981-2000 гг. минус 1961-1980 гг.).
- •Воспроизведение отклика атмосферной циркуляции на явление Эль-Ниньо.
- •Оценка воздействия
- •Среднегодовая температура поверхности океана (0С) в новой версии КМ ИФА РАН.
- •Пространственная температура (0С) в новой версии КМ ИФА РАН (белые кружки) и эмпирические
- •Модель
- •Эль-Ниньо
- •Зонально-осредненное изменение приповерхностной температуры при удвоении содержания СО2 в
- •Отклик климатической системы на увеличение (1% в год) СО2.
- •Возможные изменения зимней температуры приземного воздуха в конце XXI века (осредненной за период
Лекция 14. Модели общей циркуляции атмосферы и океана
- основа теории климата, которая включает:
1. Математическую теорию климата:
-создание теории устойчивых аттракторов климатических моделей;
-исследование структуры аттракторов климатических моделей;
-развитие теории чувствительности климатических моделей (линейные приближения для различных моментов, численное исследование линейной теории отклика на малые возмущения, оптимальные возмущения, алгоритмы построения оператора отклика);
-теорию управления диссипативными системами (управление климатом).
2. Климатические модели:
-развитие параметризации физических процессов (стохастические параметризации);
-совершенствование современных моделей атмосферы и океана;
-разработку региональных моделей климата;
-разработку методов оценки последствий изменений климата для природной среды;
-создание моделей средней и верхней атмосферы для решения задач, связанных с «космической погодой».
3. Численные методы:
-разработка теории аппроксимации уравнений гидротермодинамики на аттракторах (аттрактор представляется как множество и на нем аппроксимируется мера);
-аппроксимация динамики климатической системы на аттракторах;
-разработка схем с заданной групповой симметрией;
-построение и использование пространственно-временных адаптивных сеток;
-разработка вычислительных технологий, ориентированных на массивно-параллельные вычислительные системы.
МОЦАО – должна правильно описывать отклик на малые внешние возмущения, т.к. используется для прогноза (экстраполяции).
Принципы построения моделей
-локально справедливы уравнения классической равновесной термодинамики;
-для описания динамики атмосферы и океана справедливы уравнения Навье-Стокса для сжимаемой жидкости;
-на практике используются замкнутые уравнения Рейнольдса, полученные при усреднении уравнений Навье-Стокса;
-эффекты процессов подсеточных масштабов (меньше масштаба осреднения) выражаются через характеристики процессов крупных масштабов;
-описание крупномасштабных процессов производится в приближении гидростатики: вертикальный градиент давления уравновешивается силой тяжести (постоянство радиуса Земли, пренебрежение вертикальными составляющими Кориолиса, выполняется закон сохранения энергии).
Основные процессы подсеточных масштабов:
-перенос излучения (коротковолновой и длинноволновой радиации);
-фазовые переходы влаги и процесс локального осадкообразования;
-конвекция;
-пограничные и внутренние турбулентные слои;
-мелкомасштабная орография;
-волновое сопротивление (взаимодействие мелкомасштабных гравитационных волн с основным потоком);
-мелкомасштабная диссипация и диффузия;
-мелкомасштабные процессы в деятельном слое суши.
Основные уравнения составляющих (блоков) климатической системы
А.Уравнения блока атмосферы Уравнения движения
1). Уравнение неразрывности в сферической системе координат для тонкого жидкого слоя на сферической Земле (закон сохранения переносящей субстанции: воздуха, воды, льда):
|
|
r |
|
1 |
( |
v |
|
v sin |
) 0 |
t |
r |
sin |
|
|
|||||
|
|
|
|
|
|||||
2). Уравнение сохранения массы переносимой субстанции (водяного пара, газовых примесей, солей и т.д.):
c |
|
c r |
|
1 |
( |
cv |
|
cv sin |
) Qc |
t |
r |
sin |
|
|
|||||
|
|
|
|
|
|||||
t – время, ρ – плотность, с- концентрация, r – радиус, θ=90-φ – дополнение до широты φ, λ – долгота, α – радиус Земли,
v – составляющие скорости, Qc – сумма интенсивностей источников и стоков примесей в единице объема.
3) Уравнения горизонтального движения жидкой среды в тонком сферическом слое на поверхности вращающейся Земли (отражают законы сохранения количества движения среды):
|
dv |
ctg v2 |
2 cos * v |
|
|
1 |
|
|
p |
F |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где: |
|
d |
|
|
vr |
|
|
|
v |
|
|
|
|
v |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
dt |
t |
r |
|
sin |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
pF |
|
r |
|
1 |
|
|
( |
sin |
|
|
) |
ctg |
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
r |
|
sin |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
dv |
|
ctg v |
v |
|
|
2 cos * v |
|
1 |
|
|
p |
F |
||||||||
|
|
|
|
|
||||||||||||||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
pF |
|
r |
|
|
|
|
1 |
|
( |
sin |
|
|
) |
ctg |
|
|||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
r |
|
sin |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||
F –горизонтальные составляющие силы трения, выраженные через тензор напряжений трения {τji}, Ω- скорость вращения
Земли, - p -давление
4) Уравнение статики: p / r g(1 |
2 v sin / g) ( …..) – для описания экваториальных течений в океане. |
Уравнения переноса радиации
1) Уравнение энергии:
dS |
|
T |
|
1 |
|
T |
|
T |
sin |
|
S – энтропия, FT-составляющая мелкомасштабного |
|
|
Fr |
|
( |
F |
|
F |
|
) |
переноса тепла (энтропии), ε – интенсивность |
|||
dt |
r |
sin |
|
|
|
|
||||||
|
|
|
|
|
|
притока всех видов энергии к единице массы среды. |
||||||
2) Уравнение баланса энергии: |
|
|
S (1 q)Sd qSv ; |
||||||||||||
где: Sd |
cp lnT Rd ln pd |
|
const |
|
Sd, Sv – энтропии сухого воздуха и водяного пара, p – их парциальные давления, |
||||||||||
|
|
Sv |
cpv |
lnT Rv ln pv |
|
const |
|
Т – температура, q – массовая доля водяного пара; αv=0.622 – отношение |
|||||||
|
|
|
|
молекулярных масс водяного пара и сухого воздуха; ср=1000 Дж/(кг*К) и |
|||||||||||
|
|
q v pv /[ p (1 v ) pv ] |
|
срv=1810 Дж/(кг*К) – удельные теплоемкости сухого воздуха и водяного пара |
|||||||||||
|
|
|
при постоянном давлении; Rd=287 Дж/(кг*К),Rv=461Дж(кг*К) – их газовые |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
постоянные. |
|
||
3) Уравнение баланса тепла (краевое условие на подстилающей поверхности): |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AS – коротковолновое альбедо поверхности; FS, IL –падающие |
|
H |
|
(1 A )F |
I B(T ) H LE H |
|
потоки коротко и длинноволновой радиации; B(TS)=εσT4 – |
||||||||||
S |
w |
длинноволновое излучение поверхности (σ – постоянная Стефана- |
|||||||||||||
|
|
|
s S |
L |
|
|
S |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Больцмана, ε – коэффициент серости поверхности); H, HS –потоки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тепла с поверхности в атмосферу и в почву, лед и воду; Е –скорость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
испарения с поверхности; Hw – теплота плавления или замерзания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
льда и снега на поверхности. |
|
4) Связь параметров пограничного слоя с краевым условием: |
|||||||||||||||
C |
U 2 |
и |
H C |
H |
c |
p |
U ( |
h |
T ) |
|
τ – напряжение трения; Сτ , СН –коэффициенты трения и |
||||
|
|
|
|
|
|
|
|
s |
|
теплообмена; h – уровень; U – скорость ветра. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Уравнения переноса влаги и примесей
1)Уравнение состояния влажного воздуха:
[Rd (Rv Rd )q] T Rd T
2)Уравнение переноса водяного пара:
p – парциальное давление, Т – температура, q – массовая доля водяного пара; Rd=287 Дж/(кг*К),Rv=461Дж(кг*К) –
газовые постоянные сухого воздуха и водяного пара..
dq |
|
F q |
|
1 |
( |
F q |
|
F q sin |
) m |
|
|
|
r |
|
|
|
|
|
|||
dt |
r |
sin |
|
|
||||||
|
|
|
|
|
3) Уравнение баланса воды или льда:
dq |
w |
|
F w |
|
1 |
|
F w |
|
F w sin |
|
|
|
r |
|
|
( |
|
|
|
) m n |
|
|
|
r |
sin |
|
|
|||||
dt |
|
|
|
|
||||||
Fiq – составляющие мелкомасштабного потока водяного пара; m – удельная скорость конденсации (испарения при m<0).
qw – удельная водность; Fiw – составляющие мелкомасштабного потока водности; n=әQw/ρәr – скорость выпадения осадков; Qw =-ρqwWср – плотность вертикального
потока воды (снега или льда) со средней скоростью выпадения Wср, взвешенной по спектру массы капель, снежинок или
кристаллов льда.
4) Уравнение баланса влаги (краевое условие на подстилающей поверхности):
Es |
P E Ew |
ES – скорость удаления влаги с поверхности стоками или просачиванием воды в |
|
почву; Р – скорость выпадения осадков; |
|||
|
|
Е– скорость испарения с поверхности; Еw – масса льда и снега на поверхности.
5)Связь параметров пограничного слоя с краевым условием:
E CE U (qh qs ) |
СЕ –коэффициент испарения; h – уровень, U – скорость ветра. |
Б. Уравнения блока океана
1). Дополнительно к уравнениям движения атмосферы (1),(3),(4) добавляется уравнение состояния
морской воды:
w w (T , p, s)
w w0 |
w0 [ 0 (T T0 ) 0 (s s0 )] |
ρw – плотность морской воды; s – соленость. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
Уравнение энергии: |
|
|
|
|
|
|
|
|
|
|
|
|
ηw(T,p,s) - энтропия морской воды; |
|||||||
|
d w |
cp dT /T dp / ds / T |
|||||||||||||||||||
|
α – коэффициент термического расширения; |
||||||||||||||||||||
3) |
Уравнение неразрывности: |
|
div(v) |
0 |
|
μ(Т) – химический потенциал морской воды. |
|||||||||||||||
|
|
|
|||||||||||||||||||
4) |
Условие «непротекания» воды через поверхность r=ξ(t,θ,λ): |
||||||||||||||||||||
|
vr |
|
|
v |
|
v |
|
|
|
|
1 |
|
(P E |
Ew ) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
t |
|
sin |
w |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
5) |
Уравнение баланса соли: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
[F s |
s(P E E |
w |
)] |
r 0 |
0 |
|
|
|
Fr – вертикальный поток соли в глубину |
||||||||||
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6) |
Система уравнений для верхнего слоя океана (при подобии профилей Т(r) и s(r)): |
||||||||||||||||||||
T(r)= |
|
{ |
Ts |
ξ≥r≥-h0 – глубина слоя перемешивания |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h1 – глубина нижней границы сезонного термоклина, |
|||
|
|
|
Ts |
- (Ts-T1)FТ[(h0+r)(h0-h1)]-h0 ≥r≥-h1 |
Т1 – температура на нижней границе термоклина. |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||
В. Поверхность суши и гидрология
-Уравнение баланса энергии поверхности (водяной пар, теплопроводность почвы).
-Системы уравнений для количественного описания движения поверхностных и подземных вод.

Г. Снежный покров и морские льды |
|
|
|
|
|
|
||||||||||||||||||||
Модель снежного покрова |
|
|
|
|
|
|
|
|
|
|
ħ=ρshs - «водоэквивалентная» толщина снежного покрова; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) Уравнение баланса снежного покрова: |
|
|
|
|
|
|
ρs – плотность снега; hs – фактическая высота снега; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рs –.интенсивность твердых осадков; E, Ews – скорости испарения и |
||||
|
|
|
|
hs / t Ps |
E Ews |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
таяния снега; Ews=Hw/L при L=335КДж/кг – удельная теплота |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плавления льда; Hw – затрата тепла на таяние снега. |
||||
Модель горизонтально-однородной вертикальной структуры льда |
AS – коротковолновое альбедо поверхности; FS, |
|||||||||||||||||||||||||
1).Уравнение баланса тепла для слоя снега на поверхности льда: |
||||||||||||||||||||||||||
IL – потоки коротко и длинноволновой |
||||||||||||||||||||||||||
H |
|
(1 A )F |
I |
B(T ) H LE H |
|
|
|
|
|
радиации; B(T )=εσT4 – длинноволновое |
||||||||||||||||
S |
w |
|
|
|
S |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
s S |
|
|
L |
|
S |
|
|
|
|
|
|
|
излучение поверхности; H, HS –потоки тепла с |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поверхности; Е –скорость испарения с |
|
2).Уравнение теплопроводности для вертикального профиля Т: |
поверхности; Hw – теплота плавления. |
|||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
c |
T / t П |
|
/ |
z |
|
|
|
hs |
|
z |
|
|
Fs |
Пi – вертикальный поток тепла; ρ=0.917 и с=2090 |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
где: |
i |
|
i |
|
|
|
|
|
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
Дж/(кг*К) – плотность и теплоемкость льда; k – |
||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
снег |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
П |
(z) |
c |
k |
T / z F |
exp |
( )d |
0 |
|
|
|
|
|
|
|
|
коэффициент теплопроводности льда; |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
i |
|
|
|
|
i |
i |
i |
|
|
|
|
s |
|
|
|
Пi |
|
|
|
лед |
χ – коэффициент поглощения солнечной радиации |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
hi |
|
|
|
|
|
|
|
|
в слое льда не покрытого снегом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пw |
|
|
|
океан |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Краевые условия:
-на границе с атмосферой должно выполняться уравнение баланса;
-на границе между снегом и льдом непрерывны Т и потоки тепла;
-на неизвестной и подвижной нижней границе льда (z=-hi) выполняются два условия:
T / |
z h |
T |
wi |
271.8K |
[Пi ( hi ) |
Пw ( hi )]/ L Ewi |
Пw(-hi) –поток тепла из океана к границе льда |
|
(задается из динамики океана). |
||||||||
|
|
|
|
|
Модель горизонтального распределения с учетом полыней и разводий
Д. Материковые льды
1) |
Уравнение горизонтального движения (без адвективных и кориолисовых ускорений): |
|||||||||||
|
dv |
|
1 p |
|
dv |
|
1 p |
|
||||
|
dt |
|
|
|
|
F |
dt |
|
|
|
|
F |
|
|
|
||||||||||
|
|
|
|
|
||||||||
2) |
Уравнение статики: |
p / r g |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Т.к. лед не сжимаем, то его движение квазистатично и в основном сдвиговое.
Поэтому в F (силы трения) составляющие скорости движения льда ui (i=1,2,3) входят «сдвиговые» элементы тензора скоростей деформаций:
ij ( ui / x j u j / xi ) / 2
Связь между элементами тензора скоростей деформации (εij) и тензора напряжений (τij) задается соотношением как псевдопластичной жидкости:
ij |
f (T , )( ij |
ij ) |
ρ – гидростатическое давление; |
δ=1 при i=j и δ=0 при i≠j. |
Краевые условия:
-для уравнений динамики на поверхности ложа ледника должны выполняться условия прилипания;
-для ледников со слоем талой воды на дне должна обращаться в нуль нормальная к поверхности составляющая скорости;
-на поверхности ледника выполняется кинематическое условие «непротекания льда» через поверхность.
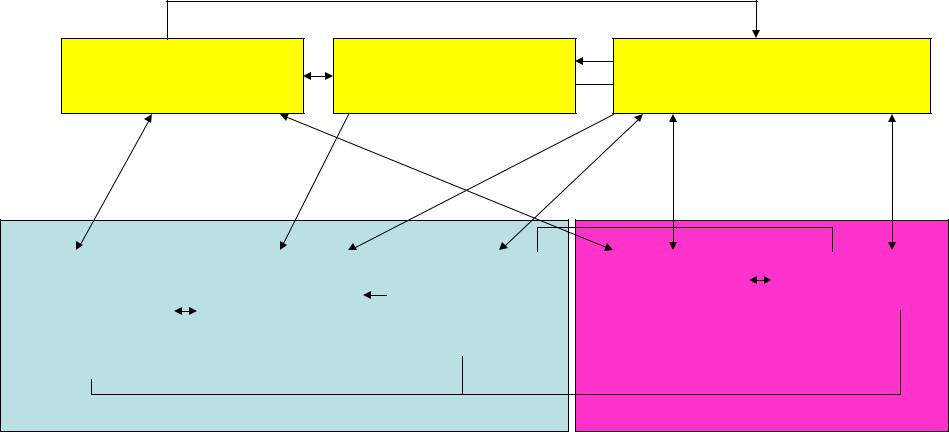
|
А Т М О С Ф Е Р А |
|
Уравнение движения |
Перенос радиации |
Перенос влаги и примесей |
1,2,3.4 |
1,2,3,4 |
1,2,3 |
Поверхностное трение |
Перенос радиации и |
Испарение и осадки |
|
явного тепла |
|
О К Е А Н |
|
С У Ш А |
Схема связи основных уравнений и краевых условий в |
||
модели общей циркуляции атмосферы и океана. |
||