БГУИР Дискретная математика КР 1 Вар 13

1. Составить таблицу истинности для формулы: ((A˄B)→C)↔(A→(B˅C))

Решение:

A	B
0	0
0	0
0	1
0	1
1	0
1	0
1	1
1	1

2. Установить эквивалентность формулы с помощью таблиц истинности

(A˅B)˄(A˅B) и (A˅B)˄ (A˄B)

Решение:

Составим таблицы истинности для заданных формул:

3. Упростить формулу: s˅(t˄s˄m)

4. Записать в ДНФ и СДНФ формулу: (A→B)→(B→A)

Используя законы логики, приведем  формулу к виду, содержащему только  дизъюнкции элементарных конъюнкций (ДНФ).

(

A

→

B

)

→

(

B

→

A

)

A	B	∨	A	B	∨	A	B

5. Записать формулу в приведенном виде (содержащем только операции ¬, ˄, ˅ над простыми переменными).

(A˄B)˅ 6. Построить полином Жегалкина для функции: (x˅y)→(x˅z)

Построим таблицу истинности данной функции:

X
0
0
0
0
1
1
1
1

7. Проверить самодвойственность функции: x↓y˅x→y.

Составим для данной функции таблицу истинности:

X
0

8. Проверить монотонность функции: .

Составим для данной функции таблицу истинности:

9. Проверить полноту системы: {x₁→x₂,x₂→x₁x₃}

Для доказательства полноты системы  необходимо проверить, что система содержит 

Таблица истинности для { x₁→x₂}:

1	1	0	1

Функция сохраняет 0 и 1.

Проверяем на самодвойственность. Результат второй строки при инвертировании не совпадает с результатом 3-ей строки. Функция не самодвойственная. Одного условия достаточно для доказательства что функция полная.

Таблица истинности для { x₂→x₁x₃}:

10. Упростить схему:

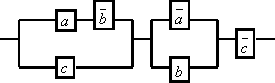
Составим функцию проводимости для схемы:

f(\

За полным содержанием данной работы обращайтесь по следующим адресам:

https://vk.com/orororr

schmuglevski@mail.ru