Кафедра301 Рациональное управление объектами теория и приложения

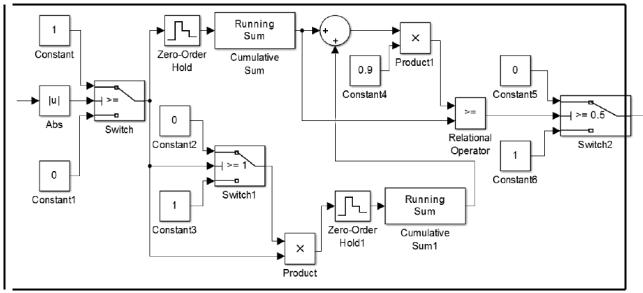
Типовая схема модуля обнаружения показана на рисунке 2.29.

Модуль

диагностирования

допустимое отклонение, то блоком Switch формируется уровень “лог 1”, если нет – то “лог 0”. Сумматорами Running Sum1 и Running Sum2 с заданным периодом квантования в интервале диагностирования суммируются числа “лог 1” и “лог 0”. Если сумма “лог 1” превышает сумму чисел “лог 1” и “лог 0”, умноженную на коэффициент доверия, то на выходе модуля диагностирования устанавливается сигнал уровня “лог 1”, свидетельствующий о наличии дестабилизации в соединении «УМ + ДМ + ТГ».

Алгоритмы работы остальных модулей диагностирования аналогичны, за исключением незначительных отличий в части допусков пороговых отклонений контролируемых параметров и использовании дополнительных параметров для формирования достоверных результатов диагноза.

Для моделирования нештатных режимов функционирования вводили следующие виды дестабилизирующих воздействий: обрыв напряжения питания усилителя мощности; изменение коэффициентов преобразования усилителя мощности, двигателя-маховика и тахогенератора.

На рисунке 2.30 изображены графики состояния параметров в интервалах времени номинального режима функционирования при обрыве напряжения питания и после автоматического восстановления работоспособности по результатам диагностирования.

80

г

в

д е

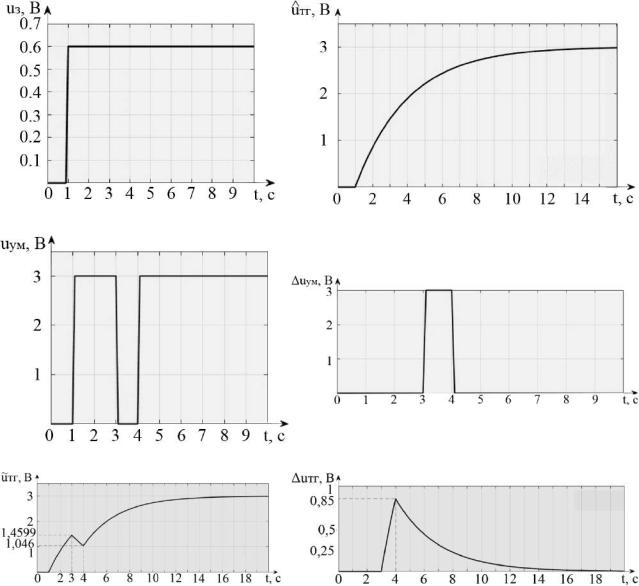
Рисунок 2.30 – Графическое изображение процессов диагностирования

ивосстановления работоспособности при обрыве напряжения питания УМ:

а– задающее воздействие; б – переходная характеристика эталонной модели;

в– напряжение питания УМ; г – диагностирование напряжения питания УМ;

д– переходная характеристика привода; е – диагностирование выходного

параметра привода uтг (t)

Графики отражают следующие параметры и события:

1) на вход электромаховичного привода и эталонную модель одновременно на первой секунде поступает задающий сигнал uз(t) (см. рисунок 2.30, а);

2) напряжение uум (t) на выходе усилителя мощности (см. рисунок 2.30, в) соответствует эталонному;

81

3) в интервале с первой по третью секунду электромаховичный привод функционирует в номинальном режиме uтг (t) = uˆ тг (t) - uтг (t) = 0 (см. рисунок 2.30, б, д, е);

4) на третьей секунде моделируется событие обрыва напряжения питания усилителя мощности (см. рисунок 2.30, в), в результате которого изменяется поведение контролируемых параметров uтг (t) и uум (t) (см. рисунок 2.30, г, е);

на “коммутатор” (см. рисунок 2.27) формируется сигнал с уровнем «1» для отключения УМОСН и включения в работу УМР. Работоспособность

На рисунке 2.31 показаны результаты моделирования по диагностированию нештатной ситуации и восстановлению работоспособности электромаховичного привода при дестабилизации коэффициента преобразования усилителя мощности.

Управляющий сигнал uз(t) = 0,6 В на вход усилителя мощности поступает на первой секунде (см. рисунок 2.31, а). В интервале с первой по третью секунду электромаховичный привод экспоненциально набирает обороты и увеличивает величину кинетического момента.

Переходный процесс электромеханического привода соответствует эталонному поведению и поэтому сигнал отклонения uтг (t) ≡ 0 (см. рисунок 2.31, а). На третьей секунде моделируется событие уменьшения коэффициента преобразования кум с 5 до 4 (см. рисунок 2.31, б), что приводит к

82

uЗ, В

б

а

uУМ, В

uУМ, В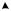

t, с

t, с

в

г

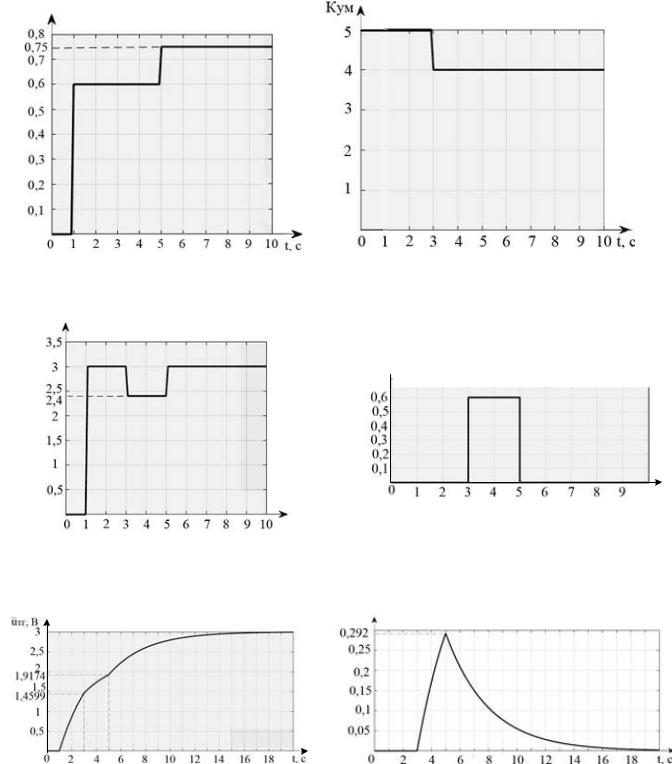
Рисунок 2.31 – Графическое изображение процессов диагностирования

ивосстановления работоспособности при изменении кум:

а– задающее воздействие; б – изменение коэффициента передачи;

в– изменение напряжения УМ; г – диагностика изменения напряжения УМ;

д– восстановление работоспособности; е – погрешность напряжения ТГ

83

Блок диагностирования по отклонениям uтг (t) и uум (t) обнаруживает

наличие и место отказа. Идентифицируется вид отказа коэффициента преобразования кум.

Признак дестабилизации кум с уровнем “1” поступает в блок параметрической подстройки, в котором формируется необходимое приращение

Момент приращения uз(t) показан на рисунке 2.31, а, восстановление параметров усилителя мощности и тахогенератора до эталонных величин – на рисунке 2.31, в, д.

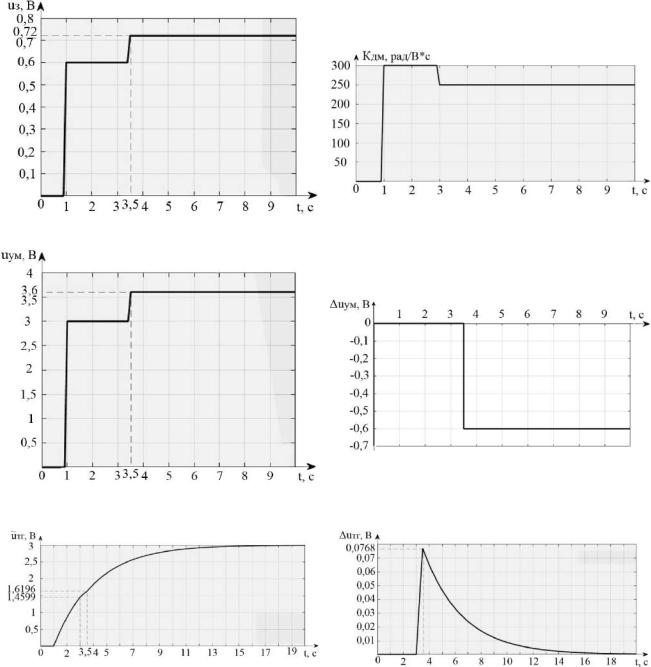
На рисунке 2.32 изображено графическое состояние параметров электромаховичного привода при дестабилизации коэффициента преобразования двигателя-маховика.

Управляющий сигнал uз(t) поступает на вход УМ на первой секунде. В интервале с первой по третью секунды параметры привода соответствуют эталонным величинам. На третьей секунде моделируется событие уменьшения коэффициента преобразования двигателя-маховика кдм (см. рисунок 2.32, б), что приводит к изменению напряжений uтг (t) и uтг (t)(см. рисунок 2.32, д, е).

Так как выходное напряжение uум (t) соответствует эталонному, то блок

диагностирования определяет наличие дестабилизации в соединении «ДМ+ТГ». Дестабилизация коэффициента кдм компенсируется путем подстройки

параметра uз (см. рисунок 2.32, а) из следующих условий:

Δuум = ˆuˆкум(t)Δ- ккдм ;

дм дм

84

в

г

Рисунок 2.32 – Графическое изображение процессов диагностирования

ивосстановления работоспособности при изменении кдм :

а– задающее воздействие; б – изменение коэффициента передачи ДМ;

в – изменение напряжения УМ; г – изменение отклонения uум (k); д – восстановление работоспособности; е – изменение отклонения uтг (k)

На рисунке 2.33 показаны графики состояния параметров электромаховичного привода в интервалах времени: номинального режима

85

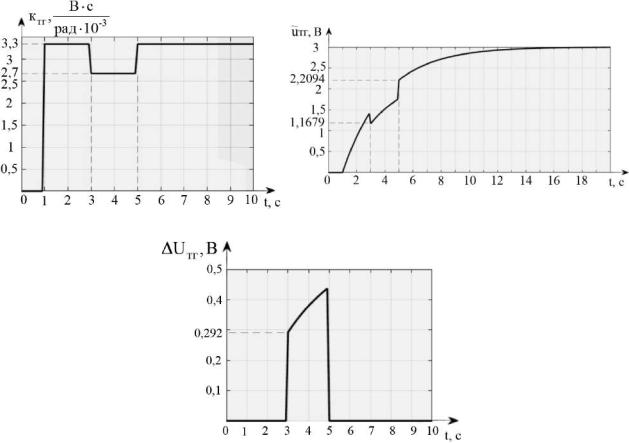
функционирования, при дестабилизации коэффициента преобразования тахогенератора и после восстановления работоспособности.

в

Рисунок 2.33 – Графическое изображение процессов диагностирования и восстановления работоспособности при изменении коэффициента передачи

тахогенератора:

а – изменение коэффициента передачи ТГ; б – восстановление работоспособности; в – погрешность напряжения ТГ

Процессы, показанные на рисунке 2.33, отражают:

1) номинальную величину коэффициента передачи ктг в интервале с первой по третью секунду;

2)дестабилизацию ктг в интервале 3 – 5 с;

3)изменение ктг путем параметрической подстройки:

ктг = ктг + ктг .

На рисунке 2.33, б изображен процесс восстановления выходного сигнала uтг (t) блока маховичного механизма при дестабилизации ктг.

86

Выводы

1.В результате проведенных исследований получены номинальные и функциональные диагностические модели электромаховичного привода как объекта автоматической стабилизации.

2.Разработаны алгоритмы обнаружения дестабилизации, поиска места дестабилизации и определения вида дестабилизации.

3.Исследованы алгоритмы восстановления работоспособности электромаховичного привода по результатам диагноза.

4.С помощью численных методов проведено моделирование электромаховичного привода в номинальных и нештатных режимах функционирования с восстановлением работоспособности.

5.В результате вычислительного эксперимента установлено, что время процедуры диагностирования и восстановления работоспособности намного меньше времени переходного процесса объекта автоматической стабилизации. Это свидетельствует об эффективности используемых методов и о принципиальной возможности рационального управления блоком электромаховичных приводов при различных дестабилизирующих воздействиях.

87

космыслению открытых явлений и снова

кпрактике, киспользованию добытых знаний.

Н. Н. Моисеев (1917 − 2000) − известный советский и российский академик, основоположник машинного моделирования динамики биосферы

Ударостойкие беспилотные летательные аппараты − это новый класс малогабаритных летательных аппаратов вертикального взлёта. Исследование динамики движения таких аппаратов как объектов рационального управления невозможно без различного рода моделей. В главе представлены модели, отражающие штатные и нештатные режимы функционирования.

3.1 Устройство и принцип действия ударостойкого летательного аппарата

Ударостойкий летательный аппарат (ЛА) представляет собой аппарат вертолетного типа с двумя соосными воздушными винтами фиксированного шага и противоположного вращения, приводимыми в движение каждый своим валом электрического двигателя постоянного тока, имеющего два соосных и раздельно управляемых ротора противоположного вращения (рисунок 3.1). Питание электродвигателя – от аккумулятора. ЛА имеет две отклоняемые управляющие поверхности для продольного и бокового управления. Отклонение каждой управляющей поверхности осуществляется своей электрической рулевой машинкой. Управляют ЛА с помощью системы автоматизированного управления, работающей в режимах автоматического управления и ручного радиоуправления.

Защитная оболочка − это силовая пространственная стержневая конструкция. В защитной оболочке шарнирно закреплены наружное и внутреннее кольца карданового подвеса. Все шарниры свободные, в результате чего ЛА может свободно вращаться относительно защитной оболочки.

88

В терминах механики летательный аппарат − это механически изменяемая материальная система нескольких твердых тел, которые в рамках рассматриваемой задачи абсолютно твердые, т. е. деформации этих тел не учитываются. Такая материальная система может быть представлена двумя группами материальных тел. Первая группа − собственно ЛА, вторая − защитная оболочка в виде усеченного икосаэдра с кардановым подвесом, где шарнирно закреплён ЛА.

Рисунок 3.1 – Внешний вид ударостойкого летательного аппарата

Таким образом, изучаемый объект при его движении в воздухе − это свободная материальная система с изменяющимися частями и параметрами:

1)угловые скорости вращения роторов двигателя и их кинетические моменты;

2)угловое положение рулевых поверхностей и связанное с этим изменение положения центра масс ЛА и его моментов инерции. В первом приближении изменением положения центра масс ЛА и его моментов инерции можно пренебречь ввиду малой массы рулевых поверхностей;

3)угловое положение ЛА в кардановом подвесе и связанные с этим изменения положения центра масс ЛА в кардановом подвесе, а также положения центра масс системы и моментов инерции системы;

4)угловое положение колец карданова подвеса и защитной оболочки и связанное с этим изменение моментов инерции.

Неизменны следующие параметры:

1)масса системы, ЛА, колец карданова подвеса и защитной оболочки;

89