Фотоэффект

1. Частота (длина волны) красной границы 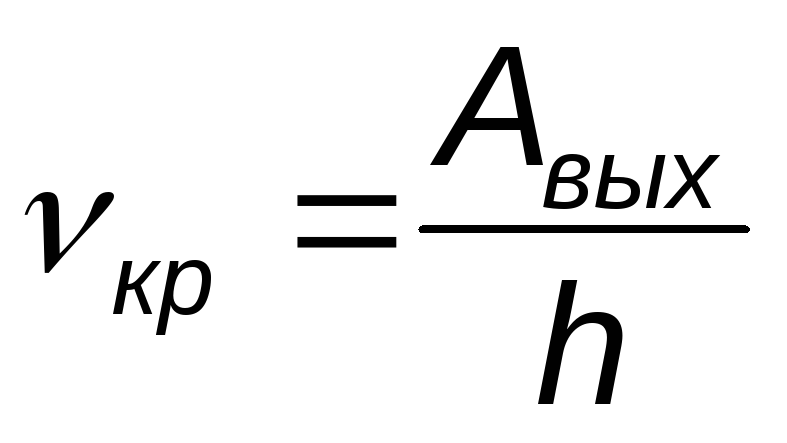Пример 1: На фотокатоде с работой выхода А= 1,3 эВ получили вольтамперные характеристики №№ 1, 2 и 3. Найти частоту падающего света для вольтамперной характеристики № 2. Пример 2: Найти длину волны красной границы фотоэффекта (в нм) для свинца.

2. Формула Эйнштейна для внешнего фотоэффекта Пример: На фотокатоде в опытах №№ 1, 2 и 3 получили вольтамперные характеристики (см.рис.). Определить максимальную кинетическую энергию фотоэлектронов в опыте № 1 (в 10^-19 Дж):

3. Зависимость тока насыщения от освещенности катода Пример: На фотокатоде в опытах №№ 1, 2 и 3 получили вольтамперные характеристики (см.рис.). Найти отношение освещенностей фотокатода в опытах № 1 к № 3

Пример : На фотокатоде в опытах №№ 1, 2 и 3 получили вольтамперные характеристики (см.рис.). Найти отношение максимального числа фотоэлектронов в опытах № 1 и № 3

Волновые свойства частиц.Квантовая физика.

1. Длина волны де-Бройля Примеры: а. Найти импульс частицы с длиной волны де-Бройля λ_Б= 0,21 нм импульс (в 10^-25 кг•м/с). в. Найти длина волны де-Бройля для протона, движущегося со скоростью V= 1.0 Мм/с, (в нм ) с. Какая из частиц (α, нейтрон,протон, электрон) обладает наибольшей длиной волны де Бройля. Скорости частиц одинаковы.

2. Стационарное уравнение Шредингера (узнавание) , где Е – полная энергия, U – потенциальная энергия Стационарным уравнением Шредингера для электрона в водородоподобном ионе является уравнение:

3. Энергия квантового гармонического осциллятора 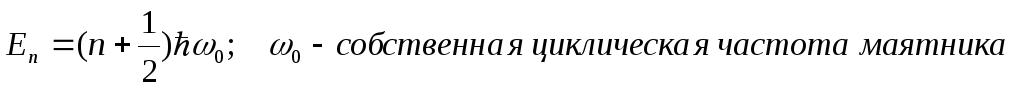Пример: какую энергию имеет квантовый гармонический осциллятор с частотой ω = 1.5х10¹⁵ рад/с на основном квантовом уровне.

4. Максимальное число электронов в атомном слое N=2n², где n – главное квантовое число Пример: Найти максимальное число электронов в шестом слое атома (72)

5. Фермионы и бозоны Фермио́н — частица (или квазичастица) с полуцелым значением спина. К фермионам относят кварки, электрон, мюон, тау-лептон, нейтрино. Бозо́н  — частица с целым значением спина. Пример: №1: 0 , №2: 0,5 , №3: 0,6 , №4: 0,7 , №5: 0,8 – Под каким номером стоит бозон, а под каким – фермион.

6. Спин электрона

Ядро Атома

1. Нуклоны

2. Зарядовые и массовые числа. Правила записи ядра химического элемента 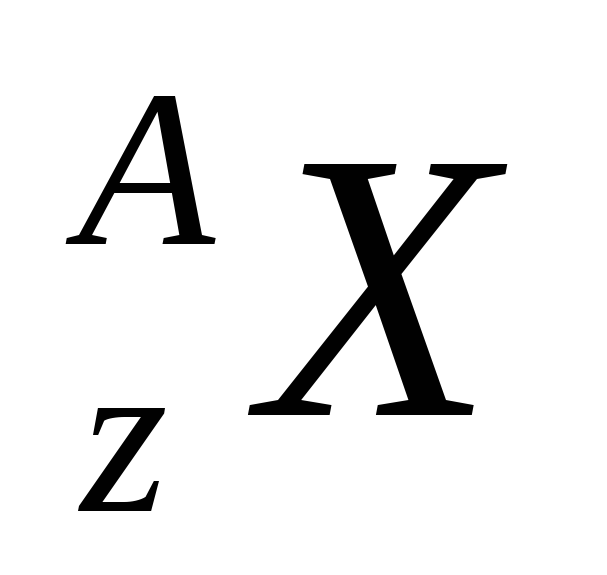; А – число нуклонов, Z – зарядовое число (число нейтронов)

3. Радиус ядра Пример: Найти отношение радиуса ядра атома вольфрама (₇₄W¹⁸⁴ ) к радиусу ядра атома железа (₂₆Fe⁵⁶ ) (1.487)

4. Магические ядра

   Магические ядра - атомные ядра, содержащие так называемые магические числа протонов или нейтронов. Z 2 8 20 28 50 82   N 2 8 20 28 50 82 126 Эти ядра имеют энергию связи больше, чем соседние ядра. Они имеют повышенную устойчивость. Ядра, содержащие магические числа протонов и нейтронов, называются дважды магическими.

5. Энергия связи. Удельная энергия связи.

Дефе́кт ма́ссы. В связи с различием в советской и зарубежной номенклатуре понятие дефекта масс не является однозначно определенным. Советская номенклатура: Дефе́кт ма́ссы — разность между массой покоя атомного ядра данного изотопа, выраженной в атомных единицах массы, и массовым числом данного изотопа. В современной науке для обозначения этой разницы пользуются термином избыток массы (англ. mass excess). Как правило, избыток массы выражается в кэВ. Зарубежная номенклатура: Дефе́кт ма́ссы (англ. mass defect) — разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, и массой покоя атомного ядра этого нуклида, выраженная в атомных единицах массы. Обозначается обычно . Согласно соотношению Эйнштейна дефект массы и энергия связи нуклонов в ядре эквивалентны: где Δm — дефект массы и с — скорость света в вакууме. Отношение энергии связи ядра Eсв к числу нуклонов A в ядре называется удельной энергией связи нуклонов в ядре  (Eсв)уд = ΔEсв / A (МэВ/нуклон)

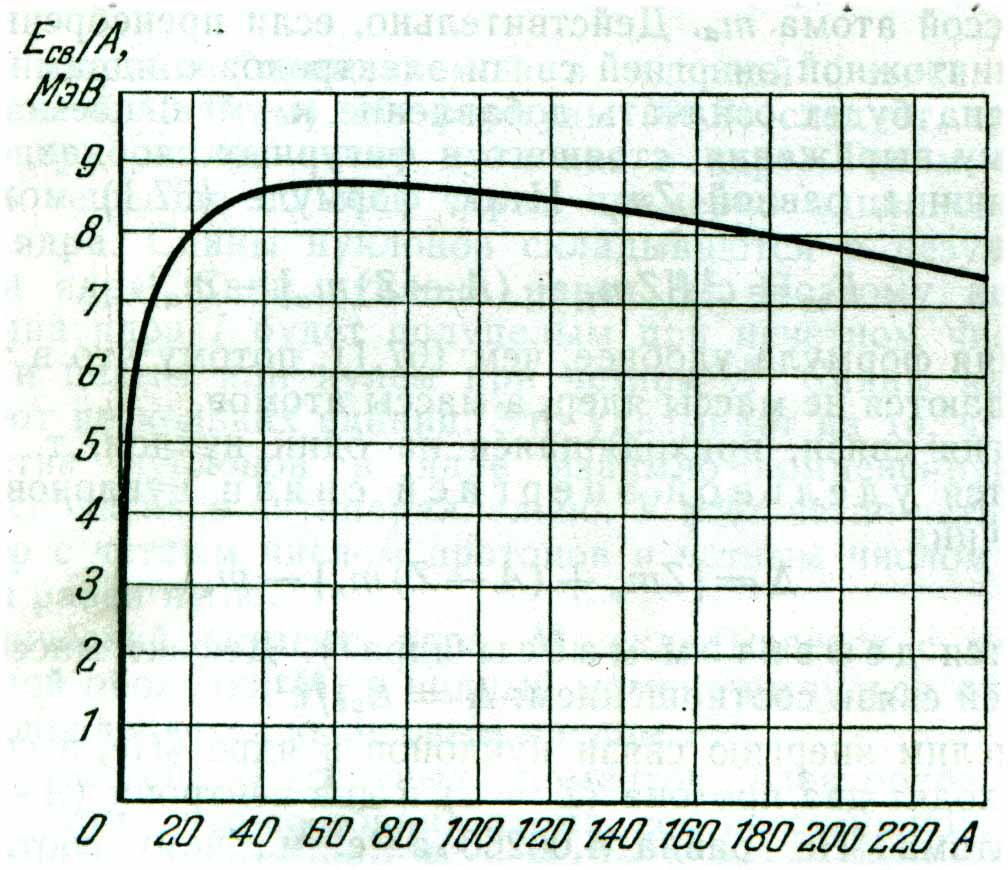
Пример:

На рисунке показана зависимость удельной энергии связи ядра от массового числа. Найти энергию связи (в Мэв) ядра с массовым числом A = 20 (160)