Лабораторная работа №1 Вариационный ряд. Его основные показатели

Задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

Статистические данные (т. е. полученные из наблюдений или опытов числа, отражающие значения изучаемого признака) записываются в форме вариационного ряда.

Примеры вариационных рядов:

1. Опыт – измерение роста 10 человек (изучаемый признак - рост)

   152

   160

   156

   156

   167

   170

   155

   152

   167

   165

2. Опыт – подсчет максимально возможного количества станков, которое может обслужить один ткач (изучаемый признак – число станков)

   Количество станков	2	4	6
   Число ткачей	2	64	154

3. Опыт – взвешивание телят (изучаемый признак - вес)

Вес	100-119	120-139	140-159	160-179
Число телят	2	20	60	18

Значение изучаемого признака в вариационном ряде называют вариантой и обозначают x_i. В примере №1 вариационный ряд состоит только из вариант, в примере №2 вариантами является количество станков, в примере №3 – вес (варианты могут задаваться в виде интервалов, при этом для расчетов берут среднее значение интервала).

Число единиц наблюдения, обладающих одинаковым значением изучаемого признака, в вариационном ряде называют частотой (весом) и обозначают f_i. В примере №1 все веса равны 1 () и поэтому они не указываются, в примере №2 весами являются число ткачей, в примере №3 – число телят.

Общее число единиц наблюдения называют объемом изучаемой совокупности и обозначают n. Для примера №1 n=10, для примера №2 n=220, для примера №3 n=100.

Для обработки данных часто используют среднее значение признака, т. е. среднее арифметическое чисел x_i. Если в вариационном ряде не указаны веса (), то находят простое среднее (). Если веса указаны, находят взвешенное среднее (_вз.).

()

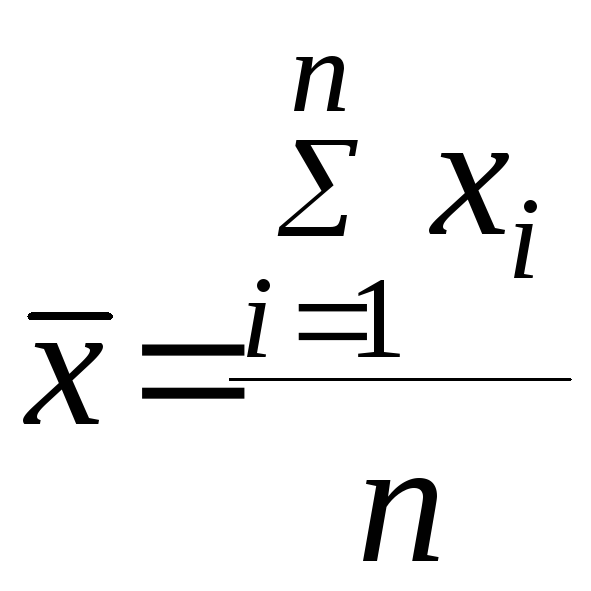
(n – число изучаемых в совокупности единиц, k – число интервалов или отдельных различных значений изучаемого признака в вариационном ряду, образовавшихся после группировки статистических данных)

Вариация – колеблемость, многообразие, изменяемость величины признака у отдельных единиц совокупности.

Основные показатели вариационного ряда (вариации)

- обобщенные характеристики степени колеблемости (вариации) признака в совокупности.

абсолютные	относительные
Размах вариации	Коэффициент осцилляции
Среднее линейное отклонение	Коэффициент вариации
Дисперсия	Линейный коэффициент вариации
Среднее квадратическое отклонение

Размах вариации (R) – разность между наибольшим и наименьшим значениями изучаемого признака.

Среднее линейное отклонение () – среднее арифметическое абсолютных значений отклонений вариант признака от средней величины признака. Как и среднее может быть простым и взвешенным.

()

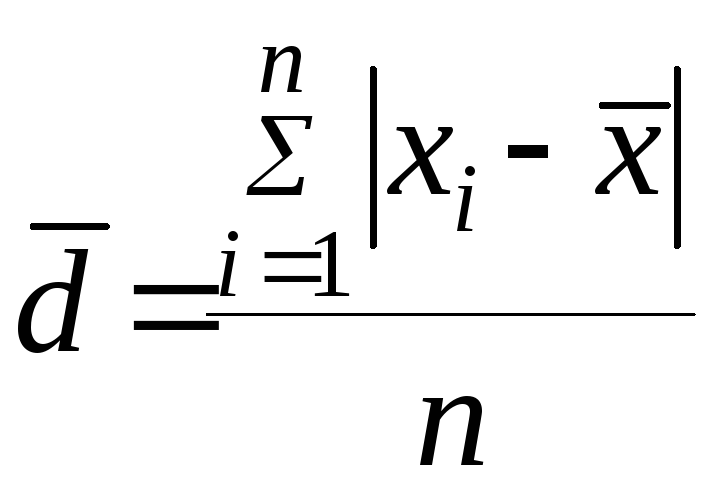
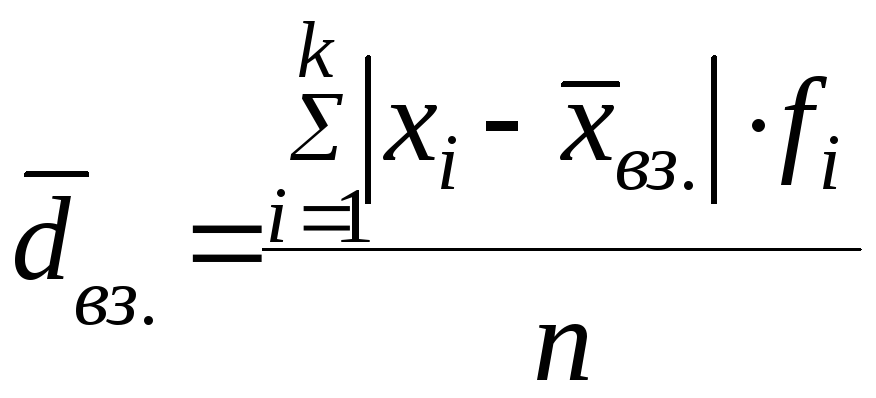Дисперсия () - средняя величина квадратов отклонений индивидуальных значений признака от средней величины признака.

()

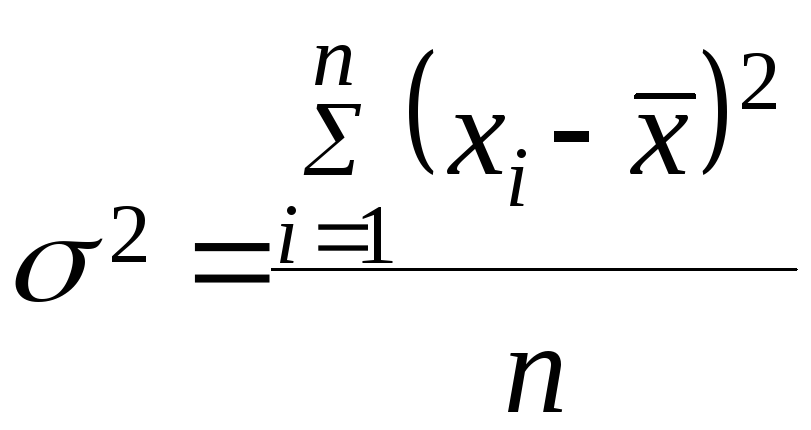
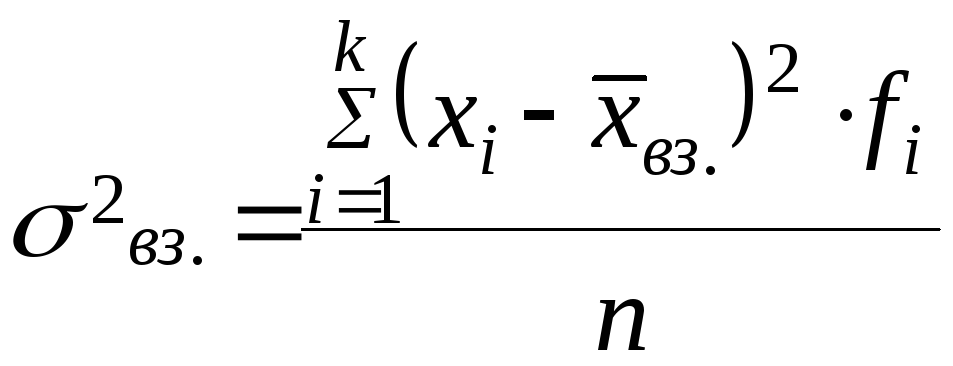Если все единицы наблюдения в изучаемой совокупности разбиты на группы, то появляются понятия групповой, межгрупповой и внутригрупповой дисперсий.

Групповой дисперсией называют дисперсию значений признака, принадлежащих данной группе, относительно среднего значения признака внутри этой группы.

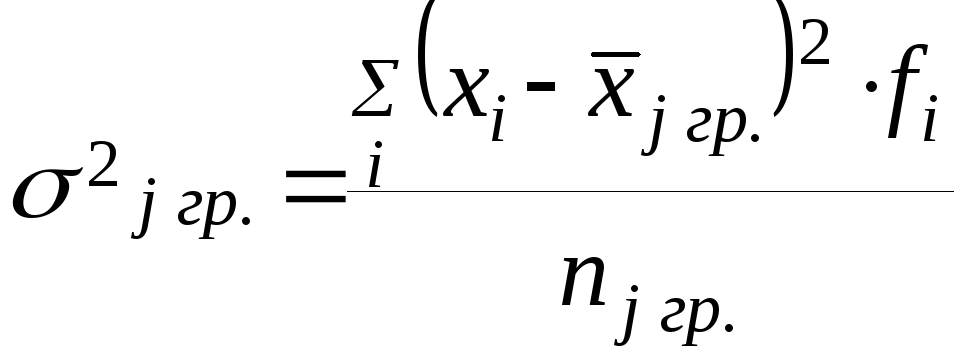- групповая дисперсия j-ой группы.

(где i – номера лишь тех единиц совокупности, которые содержатся в j-ой группе; n_{j гр.} – объем j-ой группы, - среднее значение признака внутри j-ой группы)

Внутригрупповой дисперсией называют среднее арифметическое всех групповых дисперсий данной совокупности.

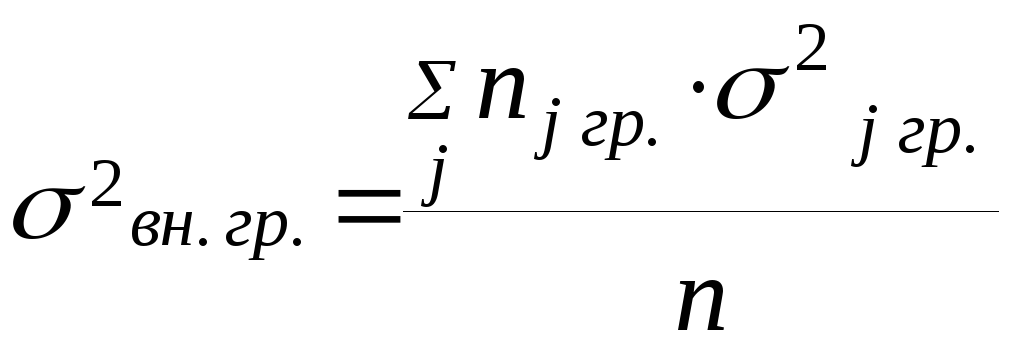(где n – объем всей совокупности, - групповая дисперсия j-ой группы, j – номера групп)

Межгрупповой дисперсией называют дисперсию средних значений признака в каждой группе относительно среднего значения признака во всей совокупности.

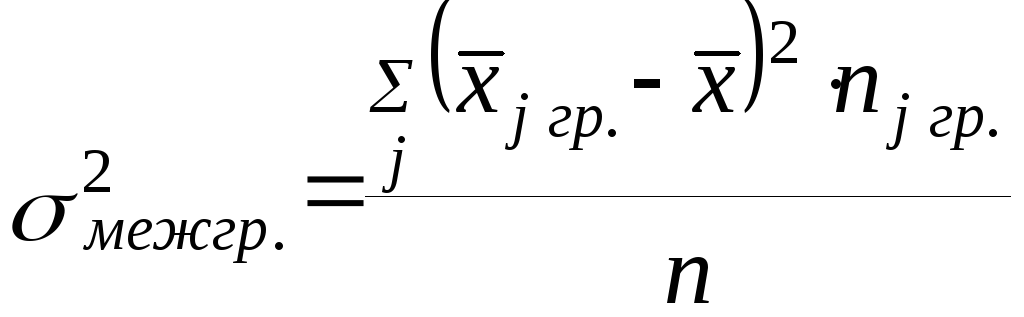
(где n – объем всей совокупности, j – номера групп, - среднее значение признака внутри j-ой группы, n_{j гр.} – объем j-ой группы)

Общей дисперсией называют дисперсию значений признака всей совокупности относительно среднего значения признака во всей совокупности.

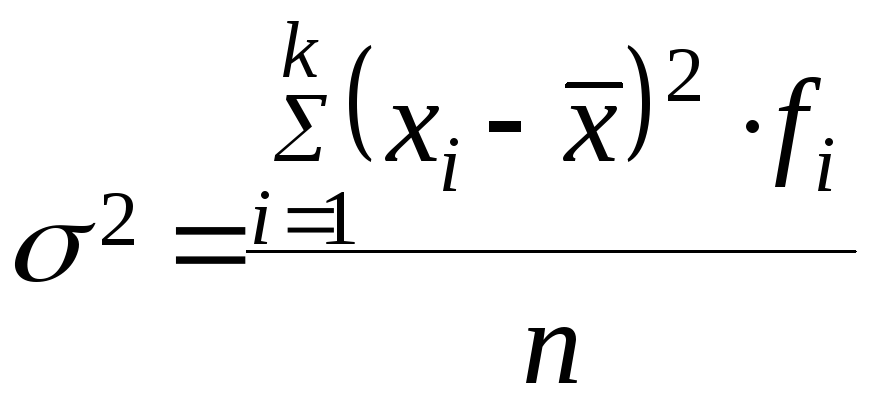
Теорема

Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:

= _вн.гр.+ _межгр.

Среднее квадратическое отклонение () – квадратный корень из дисперсии. Оно выражается в тех же единицах измерения, что и сам признак (дисперсия же выражается в квадратных единицах измерения признака). Найдя , все единицы наблюдения можно разбить на три группы:

• Со средним значением признака

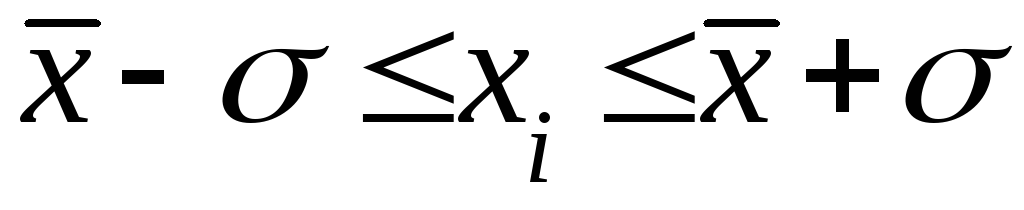
• Со значением признака выше среднего

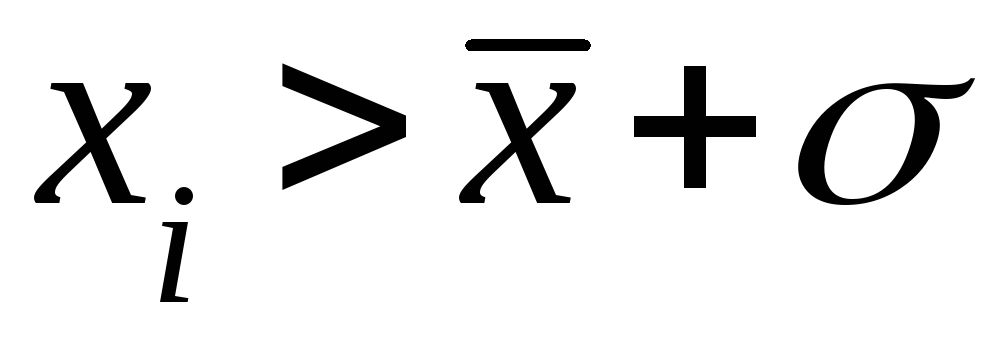
• Со значением признака ниже среднего

Относительные признаки вариации используются при сравнении колеблемости различных признаков в одной совокупности или одного признака в нескольких совокупностях.

Коэффициент осцилляции (V_R) – процентное отношение размаха вариации к средней величине признака.

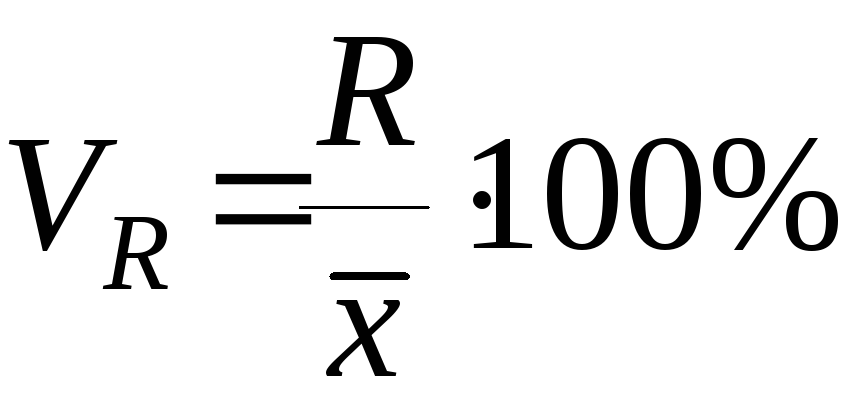
Коэффициент вариации (V_) - процентное отношение среднего квадратического отклонения к средней величине признака. Если коэффициент вариации не превышает 33%, то совокупность считается однородной.

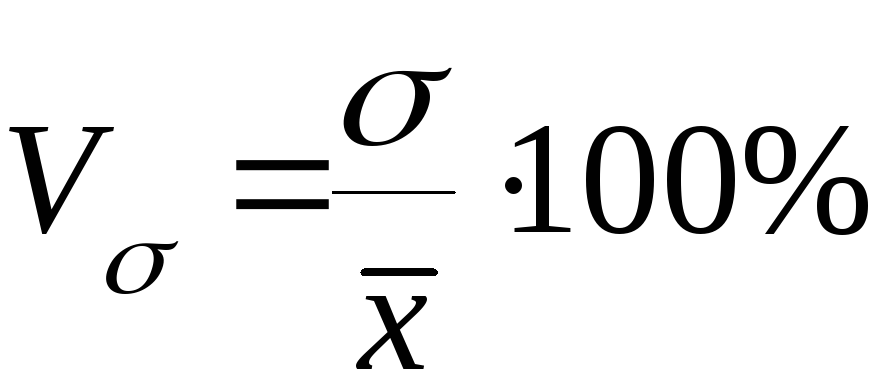
Линейный коэффициент вариации () - процентное отношение среднего линейного отклонения к средней величине признака.

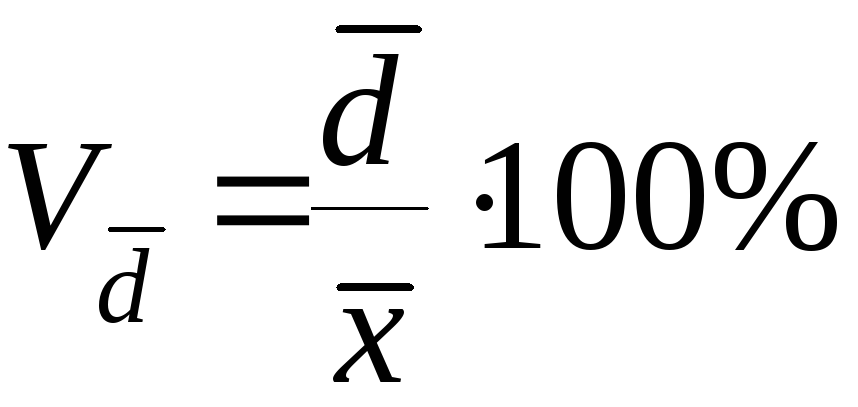
Анализ рядов распределения наглядно можно проводить на основе их графического изображения. Для этой цели строят графики - полигон, гистограмма, огива, кумулята.

Полигон – ломаная линия, отрезки которой соединяют точки (x₁,f₁), (x₂,f₂), . . .,(x_n,f_n), где x_i – варианты, f_i – частоты. Используется для изображения дискретных вариационных рядов (варианты принимают только целые значения).

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x₁,w₁), (x₂,w₂), . . .,(x_n,w_n), где x_i – варианты, w_i – относительные частоты ().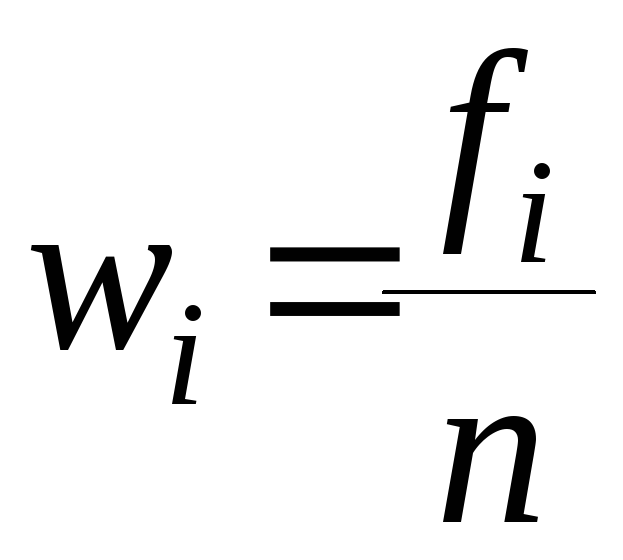

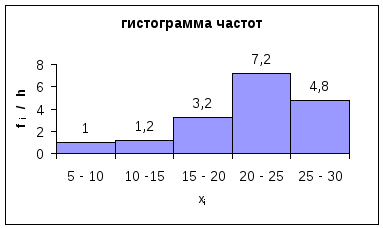
Гистограммой называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат интервалы значений признака длиною h, а высоты пропорциональны частотам соответствующих интервалов значений. Используется для изображения интервальных вариационных рядов (варианты заданы интервалами). При построении гистограммы вариационного ряда с равными интервалами по оси ординат наносят частоты, с неравными интервалами - плотность распределения (частота интервала, деленная на длину интервала).

Если середины верхних сторон прямоугольников соединить ломаной, то получим полигон.

Пример:

	xi	fi/h
	5-10	1
	10-15	1,2
	15-20	3,2
	20-25	7,2
	25-30	4,8
	h=	5

При помощи кумуляты изображается ряд накопленных частот (). Это ломаная линия, отрезки которой соединяют точки (x₁,m₁), (x₂,m₂), . . .,(x_n,m_n), где x_i – варианты, m_i – накопленные частоты.

Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, получим огиву.