§3. Отражение и преломление света на сферической поверхности раздела

Рассмотрим прохождение света через сферическую границу раздела двух сред с показателем преломления и .

Будем рассматривать только те лучи, направление которых с нормалью к поверхности, проведенной из , составляют малые углы, так называемые параксиальные лучи.

Введем прямоугольную систему координат с началом в точке . Все расстояния, отсчитываемые от поверхности влево: «-», вправо: «+».

Вертикальные отрезки, отсчитываемые вверх: «-», вниз: «+».

Углы, отсчитываемые от «-», если их и «-», и «+»,если их и «+».

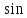Если углы отсчитываются от нормали к поверхности, не совпадают с выбранной осью системы координат, то углы между лучом и нормалью «+», если поворот луча к нормали происходит против часовой стрелки, и «-», если по часовой стрелке.

Радиус кривизны сферической поверхности «+», если центр кривизны лежит справа от начала координат, и «-», если слева.

Таким образом, выпуклая (по ходу луча) поверхность имеет , вогнутая: .

Пользуясь этими правилами знаков, рассмотрим преломление на поверхности двух лучей: 1 и 2.

1-й луч, как идущий по нормали к поверхности , не изменит направление распространения при переходе из одной среды в другую.

2-й луч, падая на под , преломляется под причем для параксиальных лучей:

Значение преломления будет иметь вид :.

Из рисунка: , .

Тогда закон преломления для луча на сферической поверхности можно записать: .

Имея ввиду, что , , .

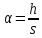Получим:

(;h)

(*)

Т.е. при преломлении параксиальных лучей на сферической поверхности остается постоянной некоторая величина , зависящая только от расстояния до истока, радиуса кривизны сферической поверхности и показателя преломления среды, где находится источник света.

Эта величина называется инвариантом Аббе.

Преобразуя (*), получим формулу для преломления лучей на сферической поверхности в виде:

=> – оптическая сила сферической поверхности.

.

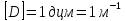Если заменить , то для случая отражения получим формулу сферического зеркала:

Величина называется фокусным расстоянием до зеркала.

Если , то , т.е. изображение, даваемое выпуклым сферическим зеркалом, всегда мнимое.

Если , то и в зависимости от значения 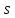изображение может быть как мнимым, так и действительным, т.е. изображение, даваемое вогнутым сферическим зеркалом, может быть либо мнимым, либо действительным.

Если , то и, следовательно, изображение, даваемое плоским зеркалом, всегда мнимое, что мы уже показали ранее.

Ход луча в выпуклом/вогнутом зеркале.

§4. Тонкие линзы. Формула линзы

Рассмотрим прохождение луча света через две сферические поверхности, расположенные так, что их центры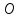 и 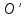лежат на одной прямой .

В соответствии с правилами знаков, радиус поверхности обозначим через , поверхности - .

Ось , проходящая через центры поверхностей, называется главной оптической осью.

Опишем ход параксиального луча для поверхности :

Инвариант Аббе: . Умножим обе части выражения на : , , , =>

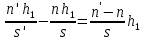(1)

Аналогично для луча, преломленного на второй поверхности:

(2)

Сложив (1) и (2), получим:

(

,

Где ,

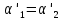
Если и , так называемая тонкая линза, то можно принять .

Тогда , где – оптическая сила линзы.

(*)

Т.к. , , то

.

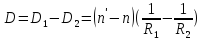Деля (*) на , получим:

,

;

Получаем, что – формула тонкой линзы.

Отсюда следует, что .

– фокусное расстояние тонкой линзы.

Если , то линза называется положительной или собирающей.

Если , то линзы называется отрицательной или рассеивающей.

Из формулы тонкой линзы следует, что при и , т.е лучи, падающие на положительную линзу параллельно главной оси, собираются в точке, называемой задним фокусом линзы. При падении на линзу справа лучей, параллельных главной оси, лучи собираются в переднем фокусе линзы на расстоянии .

Таким образом, переднее и заднее фокусные расстояния тонкой линзы равны друг другу.

Для построения изображения точечного источника в тонких линзах достаточно определить ход двух лучей.

Линейное (или поперечное) увеличение – это отношение линейных размеров изображения предмета:

ГРАФИК

, , .

При малых размерах и имеем:

;

.

В случае тонкой линзы .

Угловое увеличение:.