КУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Курсовая работа по физике

Геометрическая оптика. Поляризация.

Выполнил:

Студент 3 курса, 32 группы

Физико-математического факультета

Захарчук Б.Л.

Проверила:

Доцент кафедры физики,

Кандидат математических наук

Вервейко М.В.

Курск, 2011

Содержание

Введение

Глава 1. Геометрическая (лучевая) оптика

§1. Основные положения геометрической оптики

Явления интерференции и дифракции света показывают, что распространение света представляет собой волновой процесс.

С помощью волновой теории мы можем решать задачи о распространении света в однородной среде; через любую оптическую систему, т.е. через совокупность различных сред, ограниченных различными поверхностями и диафрагмами.

Однако в областях светотехники и оптотехники решение большого круга задач можно получить гораздо более простым путем, с помощью представлений геометрической оптики, которая оперирует понятиями определенных световых лучей.

Понятие светового луча можно получить из рассмотрения реального светового пучка в однородной среде, из которого при помощи диафрагм с отверстиями выделяется узкий параллельный пучок.

Чем меньше диаметр отверстий, тем уже выделяемый пучок, и в пределе, переходя к отверстиям сколь угодно малым, можно, казалось бы, получить световой луч как прямую линию. Однако подобный процесс невозможен вследствие явлений дифракции.

Неизбежное угловое расширение реального светового пучка, пропущенного через диафрагму диаметра , определяется углом дифракции (направление на первый ). .

Только в предельном случае, когда 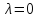, подобное расширение не имело бы места, и можно было бы говорить о луче (если , ) как о геометрической линии, направление которой определяет направление распространения световой энергии.

Таким образом, световой луч есть абстрактное математическое понятие, а не физический образ, и геометрическая оптика есть лишь предельный случай реальной волновой оптики, соответствующий исчезающе малой длине световой волны.

Соотношением 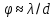показываем, что угловое отклонение, нарушающее прямолинейность распространения света в однородной среде, может быть весьма мало, если размеры отверстия велики по сравнению с .

Поэтому в реальной оптике, где-конечная величина, отступления от законов геометрической оптики должны быть тем меньше, чем больше размеры .

В основу геометрической оптики положен принцип, установленный французским математиком Пьером Ферма в 1662г. Из этого принципа вытекают законы прямолинейного распределения, отражения и преломления света.

В формулировке самого Ферма принцип гласит, что свет распространяется по такому пути, для прохождения которого ему требуется минимальное время.

Для прохождения участка пути свету требуется время , где - скорость света в данной среде. Заменив 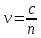, получим: .

Следовательно, время, затрачиваемое светом на прохождение пути :

.

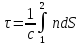Имеющая размерность длины величина называется оптической длиной пути.

В однородной среде оптическая длина пути равна произведению геометрической длины пути на показатель преломления среды . Тогда () – эта пропорциональность дает возможность сформулировать принцип Ферма следующим образом: свет распространяется по такому пути, оптическая длина которого минимальна.

Точнее, оптическая длина волны должна быть экстремальное, т.е. либо минимальной, либо максимальной, либо стационарной – одинаковой для всех возможных путей. В последнем случае все пути света между двумя точками оказываются таутохронными (требующими для своего прохождения одинакового количества времени).

Основными законами геометрической оптики являются законы о распространении световых лучей:

1. Закон прямолинейного распространения света: В однородной изотропной среде свет распространяется по прямой.

2. Закон независимости световых лучей: Световые лучи распространяются в пространстве независимо друг от друга. Пересечение лучей не влияет на характер их направления.

3. Закон отражения: Луч падающий, луч отраженный и перпендикулярный к поверхности раздела двух сред, восстановленный из точки падения луча, лежат в одной плоскости, называемой плоскостью падения. Угол падения равен углу отражения.

4. Закон преломления: Луч падающий, луч отраженный и перпендикулярный к поверхности раздела двух сред, восстановленный из точки падения луча, лежат в одной плоскости, называемой плоскостью падения. Отношение sin угла падения к sin угла преломления равно отношению скоростей света в обоих средах.

Величина называется относительным показателем преломления света относительно среды 1.

Приняв некоторую среду за стационарную (в оптике это вакуум, характеризующийся наибольшей скоростью распространения света) и введя абсолютные показатели преломления света , мы можем записать закон:

.

5. Закон обратимости световых лучей: Если свет от к идет по некоторому пути ACB, то при рассмотрении света от к во встречном направлении траектория света останется прежней.

Из принципа Ферма вытекает обратимость световых лучей. Действительно, оптический путь, который минимален в случае распространения света из точки 1 в точку 2, окажется и в случае распространения в обратном направлении. Следовательно, луч, пущенный навстречу лучу, преодолевающему путь от 1 к 2 , пойдет по тому же пути, но в обратном направлении.

Получим с помощью принципа Ферма законы отражения и преломления света.

Пусть свет падает из точки в точку , отразившись от поверхности (прямой путь прегражден экраном).

Среда, в которой проходит луч, однородна.

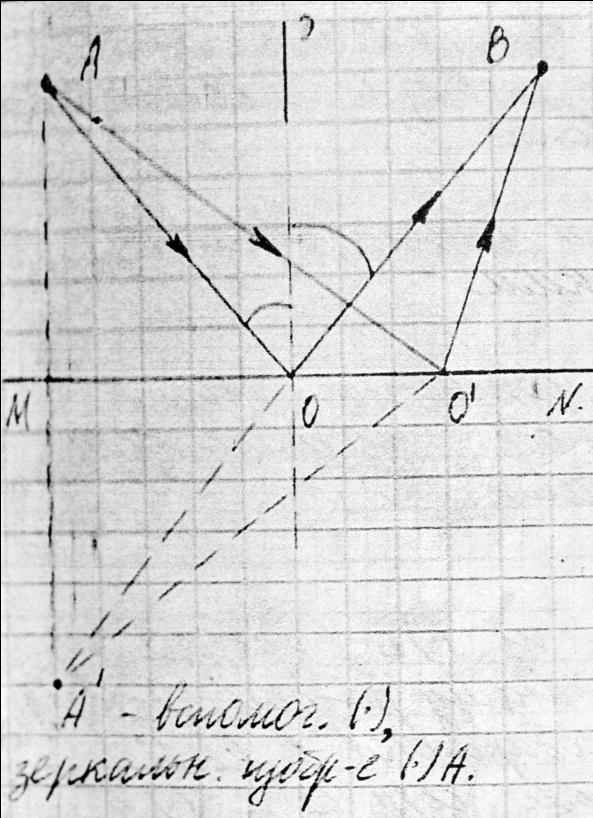
Поэтому минимальность оптической длины пути сводится к минимальности его геометрической длины.

Геометрическая длина произвольно взятого пути равна . Из рисунка видно, что наименьшей длиной обладает путь луча, отразившегося в точке O для которой угол отражения равен углу падения.

Теперь найдем точку, в которой должен преломиться луч, распространяясь от к 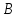, чтобы оптическая длина волны была экстремальна.

■ Для произвольного луча оптическая длина равна . Чтобы найти экстремальное значение, продифференцируем :

.

.

■.

При дальнейшем изучении геометрической оптики нам понадобится несколько понятий, связанных с особенностями описания распространения лучей света.

Если пучок лучей имеет одну общую вершину, то его называют гомоцентрическим.

Точечный источник света создает, таким образом, гомоцентрический пучок лучей.

Если лучи гомоцентрического пучка из точки , пройдя через некоторое оптическое устройство (границу раздела двух сред, неоднородную оптическую среду), вновь вобираются в точке , то гомоцентричность при этом сохраняется и в точке , называемой точкой, сопряженной с , или изображением .

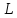Систему, сохраняющую гомоцентричность пучка, называют стигматической.

В противном случае ее называют асигматической.