1) Чебышева метод

- метод получения класса итерационных алгоритмов нахождения однократного действительного корня уравнения f(x)=0, (1), где f(х) - достаточно гладкая функция. В основе метода лежит формальное представление обратной к f(х)функции x=F(y)пo формуле Тейлора. Если - достаточно точное приближение для корня хуравнения (1), то где коэффициенты d_n рекуррентно определяются из соотношения через коэффициенты Тейлора с _n функции Полагая в (2) y=0, получают соотношение

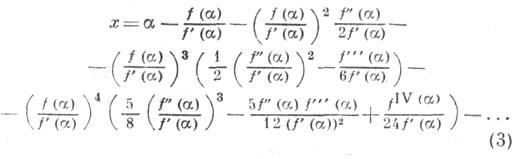
Несколько членов справа в (3) дают формулы итерационного алгоритма; так при двух членах получается Ньютона метод, а при трех членах получается итерационный метод вида

С ростом числа учитываемых в (3) членов возрастает скорость сходимости х _п к х(см. [2]). Метод может быть распространен на функциональные уравнения (см. [3]).

2) Метод простой итерации

В основе метода заложено понятие сжимающего отображения. Определим терминологию:

Говорят, что функция осуществляет сжимающее отображение на , если

1. 

2. 

Тогда основная теорема будет выглядеть так:

Теорема Банаха (принцип сжимающих отображений). Если — сжимающее отображение на , то: — корень; итерационная последовательность сходится к этому корню; для очередного члена справедливо .

Поясним смысл параметра . Согласно теореме Лагранжа имеем:

Отсюда следует, что . Таким образом, для сходимости метода достаточно, чтобы

1. 

.........

и так далее, пока

Применительно к слау

Рассмотрим систему:

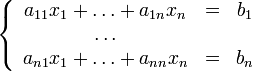
Для неё итерационное вычисление будет выглядеть так:

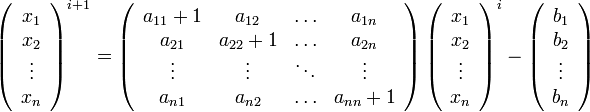
Сходимость метода будет осуществлять

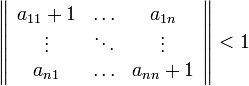
Следует отметить, что для оценки сходимости вычисляется не определитель матрицы, а норма матрицы. Поэтому в данном случае поставлены двойные вертикальные черты, а не одинарные.

Алгоритм

1. Условие 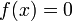преобразуется к виду 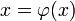, где — сжимающая

2. Задаётся начальное приближение и точность

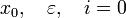
3. Вычисляется очередная итерация

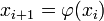
• Если 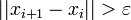, то 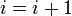и возврат к шагу 3.

• Иначе 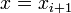и остановка.

3) Метод Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.

Описание метода Обоснование

Чтобы численно решить уравнение методом простой итерации, его необходимо привести к следующей форме: , где  — сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Решение данного уравнения ищут в виде , тогда:

В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:

С учётом этого функция определяется выражением:

Эта функция в окрестности корня осуществляет сжимающее отображение^[1], и алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:

По теореме Банаха последовательность приближений стремится к корню уравнения .

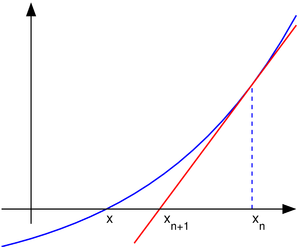
Иллюстрация метода Ньютона (синим изображена функция , нуль которой необходимо найти, красным — касательная в точке очередного приближения ). Здесь мы можем увидеть, что последующее приближение лучше предыдущего .