Гидравлическая крупность.

Так называемая гидравлическая крупность представляет собой скорость свободного падения частицы в жидкости. Иначе эту величину можно определить как скорость витания, представляющую собой такую скорость течения жидкости, при которой твердая частица остается во взвешенном состоянии, то есть, не увлекается вверх и не падает вниз в вертикально восстающем потоке жидкости.

Гидравлическая крупность одиночной частицы.

Для определения критической скорости восходящего потока (скорости витания) рассмотрим некое твердое тело (рис. 35), имеющее объем V_т и находящееся в потоке жидкости поднимающемся вертикально вверх.

Пусть:

ρ_т – плотность тела;

ρ_ж – плотности жидкости;

_ж – средняя скорость течения жидкости.

На тело действуют следующие силы:

• сила тяжести G=ρ_тgV_т, направлена вниз;

• сила Архимеда R= ρ_жgV_т, направлена вверх;

• сила сопротивления 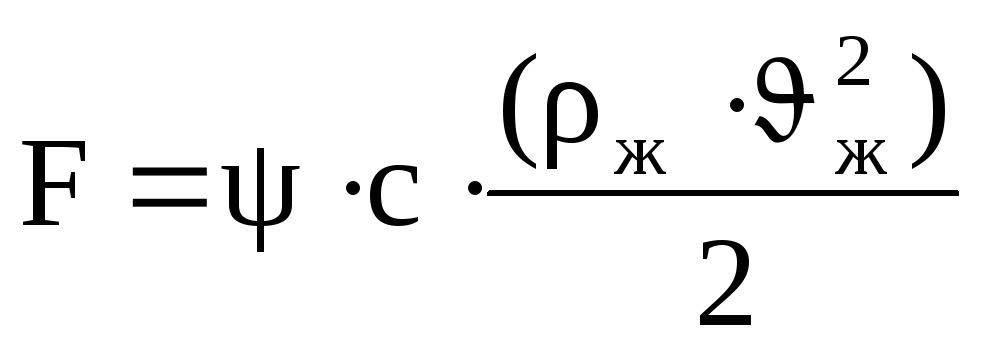, направлена вверх.

где: g – ускорение свободного падения;

ψ – безразмерный коэффициент сопротивления;

с – площадь проекциик оси движения.

При условии, что тело находится в равновесии, имеем:

R-G+F=0

или:

откуда:

Э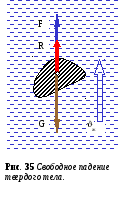та скорость (^*) и будет критической.

Из анализа полученной формулы видно, что при уменьшении разности плотностей тела и жидкости (например, утяжеление жидкости) критическая скорость (гидравлическая крупность) тела будет меньше, и, следовательно, при одном и том же значении критической скорости во взвешенном состоянии будут удерживаться тела большего «критического» размера.

Поскольку коэффициент сопротивления шара не зависит от его ориентации в пространстве, сферическая форма частиц была принята в качестве исходной при исследовании их движения в жидкости. При этом выражение приобретает вид:

где: ρ_т и ρ_ж – плотности тела и жидкости соответственно;

g – ускорение свободного падения;

d – диаметр шара;

ψ – коэффициент лобового сопротивления шара.

Зависимость коэффициента сопротивления ψ от безразмерного числа Рейнольдса (Re) при падении шаров в жидкостях носит экспериментальный характер. Число Рейнольдса можно выразить как:

где:  – скорость движения частицы;

d – ее диаметр;

 – кинематический коэффициент вязкости.

Как видим из анализа выражения (3) его неудобно использовать для практических расчетов в связи с зависимостью .

За период с начала ХХ века был предложен целый ряд эмпирических и интерполяционных формул для определения скорости свободного падения. Наиболее удобной является формула Р.Б. Розенбаум:

где: A_r – критерий Архимеда для твердого компонента, ;

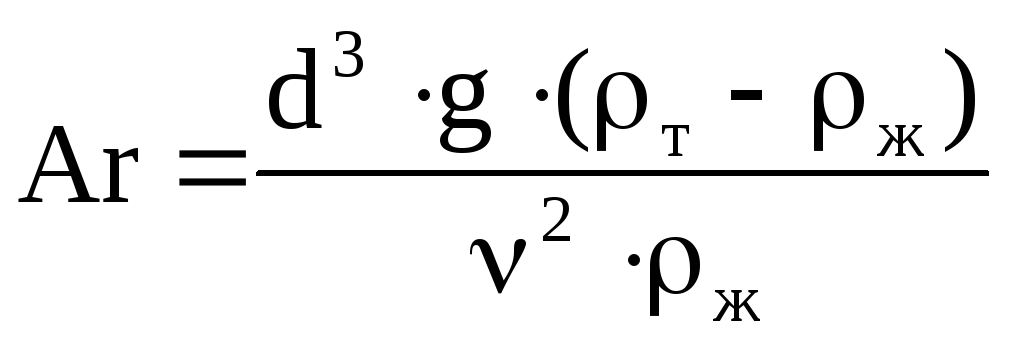ρ_т – плотность тела;

ρ_ж – плотность жидкости;

d – диаметр тела;

g – ускорение свободного падения;

 – кинематический коэффициент вязкости.

Ошибка при определении скорости свободного падения согласно этой формуле по экспериментальным данным не превышает 10% определяемой величины, что является довольно высокой точностью в области расчетов гидравлических параметров.

В реальности все минеральные частицы имеют неправильную форму. Поэтому при гидравлических расчетах вместо диаметра шара в формулах используют эквивалентный диаметр – d_э, т.е. тело заменяется шаром с равновеликим объемом:

откуда:

где: V_т – объем частицы произвольной формы.

В зависимости от плотности минеральных зерен их гидравлическая крупность различается при одинаковых размерах. Форма минеральных частиц, как правило, связанная с их минеральным составом, оказывает на гидравлическую крупность еще большее влияние. В таблице 8 приведена гидравлическая крупность различных минералов, полученная экспериментально [11].

Таблица 8.

Гидравлическая крупность различных минералов.

[по данным Ю. В. Шумилова и А. Г. Шумовского, 1975] (в см/с)

Минерал		Уд. вес, г/см3	Зерна размером
			2-1 мм	1-0,5 мм	0,5-0,2 мм	-0,2 мм
Золото		16,9	20-45	4-37	11-18	3-5
Киноварь		8,2	16-25	8-16	3-12	-
Вольфрамит		7,1	13-29	11-20	4-12	-
Касситерит		7,0	29-32	12-22	9-13	-
Шеелит		6,0	-	12-21	4-12	-
Колумбит		6,0	-	9-13	4-11	-
Магнетит		5,2	-	9-17	3-13	2-5
Пирит		5,0	20-26	15-22	9-17	-
Ильменит		4,7	-	9-20	5-14	1-4
Пикотит		4,6	-	11-12	4-11	-
Малакон		4,3	-	-	3-5	-
Рутил		4,2	-	-	3-9	-
Альмандин		4,1	16-25	8-15	3-12	-
Брукит		4,1	-	-	3-7	-
Шпинель		3,9	-	-	5-6	-
Лимонит		3,7	-	-	5-7	-
Топаз		3,6	-	6-10	5-7	-
Сфен		3,4	-	-	3-4	-
Эпидот		3,4	-	-	3-5	-
Амфибол		3,3	-	6-10	2-7	-
Турмалин		3,1	-	4-8	3-5	-
Андалузит		3,1	-	-	2-3	-
Биотит		3,1	-	5-7	4-6	-
Актинолит		3,1	-	5-7	2-6	-
Кварц	окатанный	2,6	10-21	5-7	3-6	-
	неокатанный	2,6	7-17	6-8	3-6	-
Янтарь		1,1	1-2	0,5-2	<0,1	-

Гидравлическая крупность группы частиц.

При падении в жидкости группы частиц, в реальных условиях (рис. 36), т.е. в ограниченном стенками трубы пространстве, по мере своего движения они вытесняют некоторый объем жидкости равный их собственному объему [8]. Таким образом, скорость обтекания частиц жидкостью () увеличивается, и зависит от площади сечения (С), занятой жидкостью, т.е. в конечном счете, от объемной консистенции гидросмеси. Условия свободного падения, описанные выше, называются стесненными. На отдельную частицу стеснение оказывают как стенки трубы, так и соседние частицы. Рассматриваемый эффект стеснения начинает значительно сказываться на скорости падения отдельного тела в том случае если:

,

где: D – диаметр канала, в котором движется тело,

d – диаметр рассматриваемого тела.

Гидравлическая крупность в стесненных условиях для группы частиц может быть определена как:

где: S – объемная консистенция гидросмеси;

n – степенной показатель (для турбулентного режима n=4,75)

d_ср – средневесовой диаметр частиц.

где: d_i – нижняя граница i^го класса крупности;

q_i – весовой выход i^го класса в долях единицы.

Из выражения следует, что увеличение объемной консистенции ведет к снижению гидравлической крупности. При расчетах гидротранспортных систем гидравлическая крупность твердого в стесненных условиях является важнейшим показателем, правильное определение которого позволяет, в конечном счете, найти оптимальный режим гидротранспортирования.