§7. Теорема Гаусса для вектора индукции. Уравнения электростатики для диэлектриков.

В диэлектрической среде могут присутствовать электрические заряды двух типов: "свободные" и "связанные". Первые из них не связаны с молекулярной структурой вещества и, как правило, могут относительно свободно перемещаться в пространстве. Вторые связаны с молекулярной структурой вещества и под действием электрического поля могут смещаться из положения равновесия, как правило, на очень малые расстояния.

Использование напрямую теоремы Гаусса для векторного поля при описании диэлектрической среды неудобно тем, что правая часть формулы содержит как величину "свободного", так и величину "связанного" (некомпенсированного) зарядов внутри замкнутой поверхности.

Связанные заряды, как и любые другие электрические заряды являются источниками электрического поля. Поэтому при вычислении поля в диэлектриках, наряду с плотностью ρ сторонних зарядов, нужно учитывать плотность ρ’ связанных зарядов. Следовательно, имеет место формула:

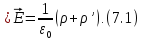
Подставив в эту формулу выражение для ρ’:

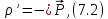
получим:

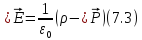
Или:

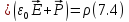
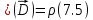
Получили формулу, которая выражает теорему Гаусса для вектора в дифференциальной форме: дивергенция вектора равна объемной плотности сторонних зарядов.

Проинтегрируем соотношение 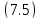по произвольному объему V:

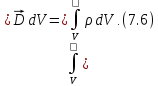
Отсюда получаем:

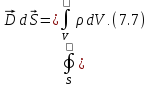
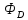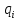Слева стоит поток вектора D через замкнутую поверхность S, справа – суммарный заряд, заключенный внутри этой поверхности. Если этот заряд образован дискретными точечными зарядами , равенство можно записать в виде:

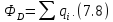
Справа стоит алгебраическая сумма сторонних зарядов, заключенных внутри поверхности S.

Таким образом, получаем теорему Гаусса для вектора в интегральной форме: поток электрического смещения через замкнутую поверхность равен алгебраической сумме сторонних зарядов, заключенных внутри этой поверхности.