Контрольные вопросы

1. Какие колебания называются гармоническими? Дать определения их основных характеристик (амплитуды, фазы, периода, частоты, циклической частоты).

2. Как представить гармонические колебания с помощью вращающегося вектора?

3. Как найти скорость и ускорение при гармоническом колебании?

4. Написать основное уравнение динамики гармонического колебания.

5. Что называется физическим маятником?

6. Вывести формулу периода колебания физического маятника.

7. Что называется приведенной длиной физического маятника?

8. Что называется моментом инерции материальной точки? Как вычислить момент инерции твердого тела? Сформулировать теорему Штейнера.

9. Вывести расчетную формулу(8).

Библиографический список

1.Трофимова, Т. И. Курс физики / Трофимова Т.И. – М.: Академия, 2004. – § 16, 140–142.

2. Савельев, И. В. Курс общей физики в 3-х т. Т.1 / И. В. Савельев.– СПб.: Лань, 2005. – § 38, 39.

3. Кингсеп, А. С. Основы физики: в 2-х т. Т. 1 / А. С. Кингсеп, Г. Р. Локшин, О. А. Ольхов. – М.: Физматлит, 2001. – Гл. 2 § 2.1, 2.2, 2.3.

4. Сивухин, Д.В. Общий курс физики: в 5-ти т. Т.1 / Д. В. Сивухин. – М.: Физматлит МФТИ, 2005. – § 39,40.

5. Курс физики: Учебник для вузов: в 2-х т. Т. 1 / Под ред. В. Н. Лозовского. – СПб.: Лань, 2006. – Гл. 1.6 § 1.33. Гл. 3.2 § 3.3, 3.7.

ЛАБОРАТОРНАЯ РАБОТА № 14.

Изучение колебаний струны

Цель работы: наблюдать собственные колебания гибкой однородной струны, натянутой между двумя неподвижными точками; исследовать зависимость скорости распространения поперечных колебаний (скорости, с которой передвигается возмущение по струне) от натяжения струны.

Оборудование: установка для изучения колебаний.

Общие сведения

Если натянуть струну и возбудить в ней колебания, то по струне побегут волны, которые, отражаясь от закрепленных концов и, складываясь друг с другом, создают сложную картину колебаний.

Рассмотрим, как распространяются волны по струне. Для этого оттянем струну, а затем ее отпустим. Созданное нами возмущение передвигается по струне, не меняя своей формы. Такое перемещающееся возмущение называется бегущей волной. В нашем случае отклонение частиц струны происходит в направлении, перпендикулярном направлению движения волны (направлению струны). Такие волны называются поперечными.

Скорость, с которой передвигается возмущение по струне, называется скоростью волны. Обозначим ее буквой u. Эта скорость не имеет ничего общего со скоростью u, которую приобретают частицы струны в процессе прохождения волны. Эти две скорости в поперечной волне перпендикулярны друг другу. Не равны и их численные величины. Скорость u зависит от того, насколько сильно была оттянута струна перед тем, как ее отпустили. Эта скорость непрерывно меняется во времени и меняет знак, когда частицы струны изменяют направление своего движения. Скорость волны u определяется только плотностью материала струны и ее натяжением.

Запишем уравнения двух плоских гармонических волн, распространяющихся вдоль оси х в противоположных направлениях:

, (1)

, (2)

где y₁, y₂ - смещение точек струны от положения равновесия, А - амплитуда, w - круговая частота колебаний, k – волновое число (k = 2π/λ).

Волна (1) перемещается в сторону увеличения х, волна (2) - в сторону уменьшения х; х – координата колеблющейся точки.

Сложив эти уравнения и, преобразовав результат по формуле для суммы косинусов, получим уравнение стоячей волны

y = y₁ + y₂ = 2Acos(kx)·cosωt. (3)

Заменим волновое число k его значением 2π/λ. Тогда уравнение (3) примет вид

y = (2Acos2πx/λ)cosωt. (4)

В стоячей волне все точки колеблются в одинаковой фазе, а их амплитуда

зависит от x. Точки стоячей волны, в которых отсутствует смещение, называют узлами, а точки, в которых амплитуда колебаний максимальна – пучностями, рис. 1.

Координаты узлов стоячей волны найдем из условия

.

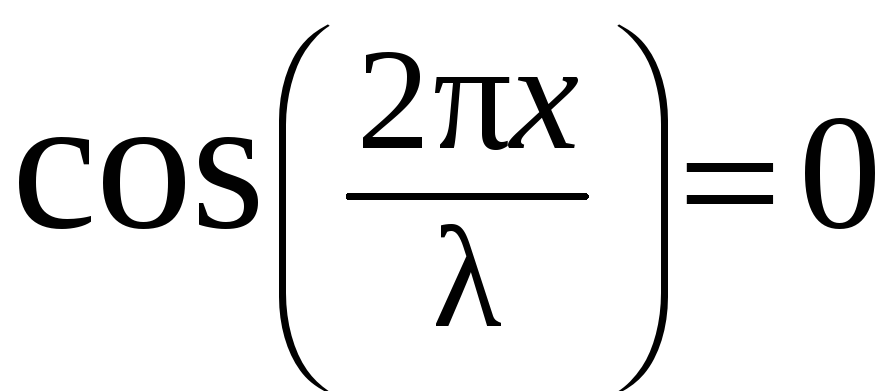Тогда

,

где n- любые целые числа (n= 0,1, 2, 3, ...). Координаты узлов имеют значения

. (5)

Аналогично получается выражение для координаты пучностей

. (6)

Из формул (5) и (6) видно, что соседние узлы или пучности в стоячей волне отстоят друг от друга на половину длины волны λ/2.

Длина волны определяется как

, (7)

где υ – скорость волны, ν – частота колебаний в герцах.

Частота колебаний, при которой на длине струны укладывается одна полуволна, называется основным тоном. Все остальные стоячие волны носят название обертонов. В нашем случае выражение (7) можно переписать

, (8)

где L - длина струны.

Тогда частота собственных колебаний струны будет

. (9)

Строгий расчет скорости распространения волны в струне приводит к дифференциальному уравнению в частных производных (к так называемому волновому уравнению). Такой расчет выходит за рамки нашего курса, поэтому для вывода применим метод анализа размерностей.

Опыт показывает, что существует зависимость частоты стоячих волн, следовательно, и скорости u, от натяжения струны, ее массы и длины. Запишем эту зависимость

, (10)

где c - безразмерный коэффициент; a, b, g - неизвестные показатели степени.

Распишем размерность правой и левой части уравнения (10):

. (11)

Равенство (11) возможно, если показатели у одноименных величин, стоящих слева и справа, равны, т.е.

. (12)

Из системы уравнений (12) находим a=-1/2, b=1/2, g=1/2.

Подставляя значения a, b, g в (11), находим

(13)

При с = 1 формула (13) совпадает с теоретической.

Итак,

, (14)

где r и d - плотность материала струны и ее диаметр, соответственно, F - сила натяжения струны.