Вопрос 7. Энергия, работа, мощность

Энергия — едина как общая количественная мера движения и взаимодействия материи. Современное знание насчитывает 15 форм движения материи, и соответственно им получается следующая классификация видов энергии, которая охватывает все варианты энергетических превращений на Земле: тепловая, механическая, электрическая, электростатическая, электромагнитная, магнитостатическая, химическая, упругостная, ядерная, гравистатическая, гравидинамическая, аннитиляционная, нейтриностатическая, нейтринодинамическая, мезонная. Подразделение энергии на виды условно, так как она является универсальной мерой различных форм движения и взаимодействия. Заметим, что природа ограничивает выбор источников энергии незначительным кругом накопленных за время существования Земли невозобновляемых (химическая энергия ископаемых органических топлив, внутренняя теплота Земли, ядерная энергия деления, термоядерная энергия) и возобновляемых ресурсов (энергия морских приливов, солнечных лучей, ветра, рек). В одних энергетических процессах форма движения материи может не изменяться (например, в процессах передачи теплоты от тел, более нагретых, к телам, менее нагретым), в других процессах преобразования энергии одна форма движения материи может переходить в иную (например, при трении механическое движение переходит в тепловое и соответственно механическая энергия преобразуется в тепловую).

Чтобы характеризовать количественно процесс передачи направленного, упорядоченного движения материи или обмена энергией между взаимодействующими телами, в механике используется понятие работы силы или, просто, работы.

Для случая прямолинейного движения тела под действием постоянной силы F, которая составляет некоторый угол а с направлением перемещения длиной s, работа этой силы равна произведению:

А = Fs cosα, H • м = Дж.

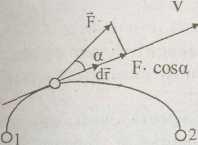
В общем случае сила может изменяться по модулю и по направлению. Силу F можно считать постоянной только в случае прямолинейного элементарного перемещения тела на величину dr (рис. 3.1). Элементарной работой силы F на перемещении называют скалярную величину , Дж, где a — угол между векторами и ; — элементарный путь. Работа силы на конечном участке траектории 12 равна:

Мощность определяет скорость совершения работы: Р = dA/dt, Дж/с = Вт.

При движении тела со скоростью под действием силы мощность, развиваемая этой силой, за бесконечно малый промежуток времени dt равна скалярному произведению вектора силы на вектор скорости:

, Вт.

Кинетическая энергия тела представляет собой энергию его движения. Движение возникает и происходит под действием силы . Энергия движущегося тела при этом возрастает на величину совершенной силой работы. Иными словами, работа dA силы на бесконечно малом пути, который тело прошло за время возрастания скорости от 0 до , идет на увеличение кинетической энергии:

dA = dE_K.

Используя для некоторой инерциальной системы второй закон Ньютона F= md/dt и умножая скалярно обе части равенства на перемещение , получим . С учетом того, что . Откуда , Дж. Итак, тело массой т, движущееся со скоростью v, обладает кинетической энергией Е_K=mv²/2, Дж.

Очевидно, что кинетическая энергия зависит только от массы и скорости тела. Траектория движения не оказывает влияния на величину Е_к .

Связь между изменением кинетической энергии материальной точки и работой силы, приложенной к ней:

dA=mνdν; .

П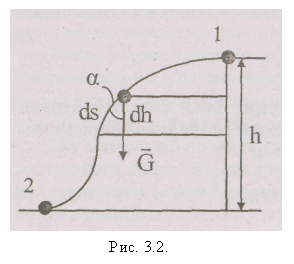усть некоторое тело перемещается в силовом поле по некоторой кривой 12. Характер сил, действующих на тело, может быть разнообразным. Это могут быть силы тяготения, электрические силы и др.

Рассмотрим работу, совершаемую при движении тела в однородном поле силы тяжести, которое имеет место вблизи поверхности Земли, где сила тяжести незначительно зависит от высоты (пока высота h мала по сравнению с радиусом земного шара. Если разбить кривую 12 на элементарные отрезки, то каждый из них можно считать прямолинейным. Элементарная работа dA, совершаемая при передвижении по отрезку ds, будет равна dA = Gcosads, где G — сила тяжести, действующая на тело; α — угол между направлением силы тяжести и направлением перемещения. Из рисунка следует, что dscosa = dh. Здесь dh — бесконечно малое изменение высоты положения тела при его перемещении на отрезок ds. Работа силы тяжести при перемещении из состояния 1 в состояние 2 будет равна

Из равенства (3.3) следует вывод о том, что работа силы тяжести не зависит от формы и длины пути, а определяется величиной вертикального отрезка h между начальным и конечным положением тела. Оказывается, что в природе есть и другие силы, помимо силы тяжести, которые обладают тем же замечательным свойством: работа по перемещению тела зависит только от положения начальной и конечной точек пути и не зависит от вида траектории и скорости движения. Такие силы, называют потенциальными. При движении материальной точки в поле потенциальных сил вводится понятие о потенциальной энергии, через разность которой определяется работа сил. Если тело перемещается из некоторой точки пространства 1 в другую точку пространства 2 и если при этом действующие на него силы совершают работу А₁₂, то для потенциальных сил эта работа зависит только от положения точек 1 и 2. Это означает, что можно ввести такую физическую величину Е_п, которая характеризует положение тела в поле потенциальных сил и которую можно назвать потенциальной энергией. Работа А_п в этом случае будет равна разности значений Е_п1 и Е_п2, которые принимает потенциальная энергия Е_п в точках 1 и 2,

А = Е_л1- Е_п2.

В том случае, когда значение потенциальной энергии в одной из точек пространства (в данном случае из двух) равно нулю, можно говорить о значении потенциальной энергии в конкретной точке.

Потенциальная энергия тела с массой т, поднятого на высоту h, равн mgh. При падении тела сила тяжести совершает положительную работу А = mgh. Потенциальная энергия при этом убывает. Работа силы тяжести при подъеме тела отрицательна, а потенциальная энергия его возрастает.

Для изолированной системы, в которой отсутствуют непотенциальные силы, например сила трения, можно утверждать, что сумма кинетической и потенциальной энергий остается постоянной, то есть Е = Е_к + Е_п = const. Это утверждение называют законом сохранения механической энергии. Из закона следует, что при переходе системы из одного положения в другое могут меняться кинетическая и потенциальная энергии. Но их сумма остается постоянной.