Уровень значимости для проверки гипотез

№ варианта	0	1	2	3	4	5	6	7	8	9
Уровень значимости р, %	1	2,5	10	5	2,5	5	1	2,5	5	10

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Перед выполнением работы необходимо ознакомиться с методами корреляционного и регрессионного анализа в соответствии с приведенным списком рекомендованных источников.

В разделе работы "Введение" студентом излагаются основные сведения о практической ценности и принципах построения регрессионных моделей.

В первом пункте основной части проводится выбор исходных данных и построение графика зависимости отклика у от фактора х.

Во втором пункте рассчитывается коэффициент корреляции между откликом у и фактором х и по критерию Стьюдента проверяется гипотеза о наличии статистически значимой линейной корреляции между указанными величинами. Если гипотеза проходит статистическую проверку, то экспериментальная зависимость может быть описана линейным уравнением регрессии, в противном случае необходимо по виду графика экспериментальной кривой выбрать одну из нелинейных моделей.

Далее производится расчет на ЭВМ коэффициентов для выбранной студентом модели, расчетного значения критерия Фишера и значений отклика у_расч в зависимости от значений факторов, соответствующих данным табл. 1.

На последнем этапе строится график у_расч=f(x), выбирается критическое значение критерия Фишера F_крит и осуществляется проверка на адекватность построенной модели.

В конце работы необходимо сделать вывод о применимости полученной модели для практических целей.

ОБЩИЕ ПОЛОЖЕНИЯ

С помощью корреляционного анализа изучается теснота взаимосвязи между откликом и факторами, а регрессионный анализ позволяет приближенно представить корреляционную связь в виде некоторого уравнения называемого уравнением регрессии. Зависимость между откликом и факторами может быть линейной или нелинейной (параболической, гиперболической, экспоненциальной или какой-либо другой). Поэтому перед выбором структуры модели необходимо выяснить форму корреляционной зависимости. В условиях малого числа факторов эта задача может быть решена графически. Но на практике часто даже после построения графика, показывающего взаимосвязь между откликом и факторами, бывает трудно с уверенностью определить, к какой именно форме (линейной или нелинейной) следует относить полученную в эксперименте кривую. Поэтому для оценки наличия линейной коррелированности величин используется линейный коэффициент корреляции, рассчитываемый по формуле:

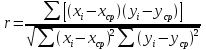, (3)

x_i - значение фактора в i-м эксперименте;

y_i - значение отклика в i-м эксперименте;

n - число экспериментов;

x_ср - среднее значение фактора х;

y_ср - среднее значение отклика у;

i=1, 2, …, n;

. (4)

Рассматриваемый коэффициент корреляции называется выборочным, является оценкой истинного коэффициента корреляции, который может быть получен для генеральной совокупности и обладает следующими свойствами:

1) -1r1;

2) чем ближе r к ±1, тем связь более тесная, чем ближе r к 0, тем связь слабее;

3) если r=±1, то связь между откликом и фактором является функциональной.

Исходя из свойств выборочного коэффициента корреляции, можно судить о тесноте связи между откликом и факторами. Задача эта очень важная, т. к. в уравнение регрессии следует включать только те переменные, которые находятся в тесной зависимости между собой. Однако прежде чем делать вывод о тесноте взаимосвязи, необходимо предварительно установить значимость выборочного коэффициента корреляции. Для этого проверяется гипотеза о равенстве нулю коэффициента корреляции в генеральной совокупности c помощью случайной величины t, имеющей распределение Стьюдента с k=(n–2) степенями свободы для заданного уровня значимости критерия:

. (5)

По таблице "Процентные точки распределения Стьюдента" (приложение 1) определяется критическое значение случайной величины t_кр.

Сравнивая расчетное значение t с критическим t_кр, делается вывод:

- если t>t_кр, то гипотеза о равенстве нулю коэффициента корреляции в генеральной совокупности не принимается, значит между откликом и фактором имеется статистически значимая линейная корреляция;

- если t<t_кр, то коэффициент корреляции в генеральной совокупности незначимо отличается от нуля, а между откликом и фактором отсутствует статистически значимая линейная корреляция.

Если принята гипотеза о значимости коэффициента корреляции, то в качестве уравнения регрессии выбирается линейная зависимость и рассчитывается коэффициент детерминации, показывающий, на сколько процентов в среднем вариация отклика объясняется за счет вариации фактора:

D = r²100%. (6)

Если коэффициент корреляции незначим, то следует предположить наличие нелинейной взаимосвязи между откликом и фактором. В контрольной работе имеется возможность выбрать при этом одно из следующих уравнений регрессии: степенная; экспоненциальная; геометрическая.

Для определения уравнения регрессии обычно используется ЭВМ. Соответствующее программное обеспечение находится в компьютерном классе института транспортной техники и сооружений, аудитория Л63.

Коэффициенты уравнения линейной регрессионной модели, имеющей вид у_расч=А+Вх, могут быть получены с помощью программы “stats.exe”. Программа позволяет также аппроксимировать экспериментальную зависимость степенной кривой вида:

у_расч=b₀+b₁x+b₂x²+…+b_mx^m, (m<6). (7)

Экспоненциальная регрессионная модель имеет вид у_расч=Ae^Bx. Геометрическая регрессионная модель имеет вид у_расч=Ax^B.

Все программные средства позволяют вычислить расчетное значение критерия Фишера и значения у_расч для построения графика зависимости отклика от фактора, полученной на модели.

Проверка гипотезы об адекватности модели по вычисленному значению критерия Фишера F осуществляется, исходя из соотношения:

F > F_кр, (8)

где F - значение критерия Фишера, полученное на ЭВМ;

F_кр - критическое значение критерия Фишера, выбираемое из таблиц "Процентные точки распределения Фишера" (приложения 2 - 5) в зависимости от заданного уровня значимости и степеней свободы v1 и v2:

v1=q, v2=n-q-1, (9)

где v1 - номер столбца;

v2 - номер строки в таблице соответствующего уровню значимости р приложения.

Гипотеза об адекватности модели подтверждается, если выполняется соотношение (8), в противном случае считается, что при выбранном уровне значимости модель неадекватно описывает поведение исследуемого объекта /12/.

ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ

Пусть в результате проведения экспериментов на моделируемом объекте были получены значения отклика у в зависимости от значений фактора х, приведенные в табл. 4 /12/.

Таблица 4