Значения экспериментальных данных

	Номер эксперимента
	1	2	3	4	5	6	7	8	9
x	1	2	3	4	5	6	7	8	9
y	10,6	13,1	15,6	16,7	21,3	20,7	22,8	29,5	34,4

Построим график зависимости y=f(x) (рис. 1).

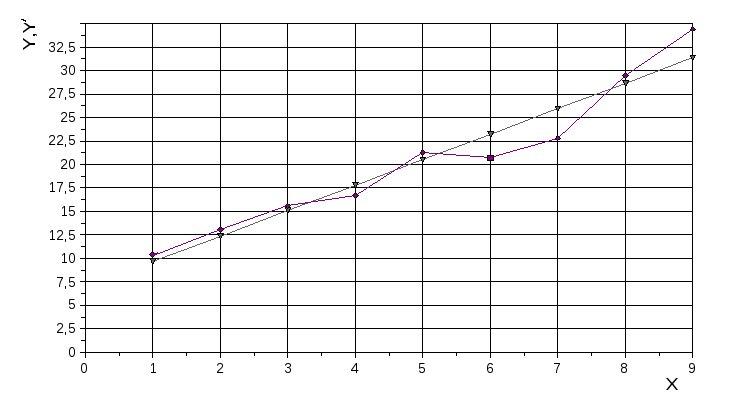
⧫ - экспериментальная зависимость;

Δ - расчетная зависимость.

Рис. 1. Графики экспериментальной и полученной на модели

зависимостей отклика от фактора

По виду графика (рис. 1) можно предположить, что между откликом у и фактором х существует приближенно линейная зависимость.

Рассчитаем средние значения х_ср и у_ср, а также коэффициент корреляции:

x_ср=(1+2+3+4+5+6+7+8+9)/9=5;

у_ср=(10,6+13,1+15,6+16,7+21,3+20,7+22,8+29,5+34,4)/9=20,5;

х₁-х_ср =1-5=-4; у₁-у_ср =10,6-20,5=-9,9;

х₂-х_ср =2-5=-3; у₂-у_ср =13,1-20,5=-7,4;

х₃-х_ср =3-5=-2; у₃-у_ср =15,6-20,5=-4,9;

х₄-х_ср =4-5=-1; у₄-у_ср =16,7-20,5=-3,8;

х₅-х_ср =5-5=0; у₅-у_ср =21,3-20,5=0,8;

х₆-х_ср =6-5=1; у₆-у_ср =20,7-20,5=0,2;

х₇-х_ср =7-5=2; у₇-у_ср =22,8-20,5=2,3;

х₈-х_ср =8-5=3; у₈-у_ср =29,5-20,5=9;

х₉-х_ср =9-5=4; у₉-y_ср =34,4-20,5=13,9;

[(x_i-x_ср)(y_i-y_ср)]=-4(-9,9)+(-3)(-7,4)+(-2)(-4,9)+(-1)(3,8)+00,8+10,2+

22,3+39+413,9=39,6+22,2+9,8+3,8+0,2+4,6+27+55,6=162,8;

(x_i-x_ср)²=16+9+4+1+0+1+4+9+16=60;

(y_i-y_ср)²=98,01+54,76+24,01+14,44+0,68+0,04+5,29+81+193,21=471,44;

Для проверки гипотезы о значимости статистической линейной связи между откликом у и фактором х рассчитаем значение случайной величины t, имеющей распределение Стьюдента:

.

По таблице (приложение 1) для числа степеней свободы k=9–2=7 и уровня значимости р=5% определим критическое значение t_кр=1,8946. Сравнивая расчетное и критическое значение, видим, что t > t_кр, значит, гипотеза о том, что связь статистически значима принимается и для построения математической регрессионной модели можно использовать линейную функцию регрессии.

Рассчитаем коэффициент детерминации:

D = r²100%=0,968²100%=93,7%,

т. е. на 93,7% в среднем вариация отклика у объясняется за счет вариации фактора х.

Используя программу “stats”, рассчитаем коэффициенты уравнения линейной регрессии А и В, расчетное значение критерия Фишера F и значения отклика у_расч для всех значений фактора х.

Для проверки гипотезы об адекватности построенной модели из таблицы (приложение 3) выберем критическое значение критерия Фишера в зависимости от числа степеней свободы v1=q=1 и v2=n-q-1=9-2=7:

F_кр=5,5914.

Сравнивая расчетное и критическое значения критерия Фишера, видим, что

F=104,236 > F_кр=5,5914, т.е. гипотеза об адекватности модели принимается, и модель вида у=6,956+2,71х может быть принята для описания исследуемого объекта.

На рис. 1 построим график расчетной зависимости. Из анализа двух кривых - экспериментальной и рассчитанной на модели - можно сделать вывод о том, что они имеют достаточно близкие значения.

ЗАКЛЮЧЕНИЕ

Регрессионная модель, как и всякая другая математическая модель, отражая основные свойства изучаемого объекта, не в состоянии полностью воспроизвести его поведение. Даже то, что исследователь наметил отразить с помощью регрессионной модели, бывает трудно сделать в силу ряда причин. Для того чтобы оценки коэффициентов уравнения регрессии оказались точными и исследователь получил ответ на вопросы о влиянии всех интересующих его факторов отдельно и во взаимодействии на отклик, необходимо специфическое расположение значений факторов, чего можно добиться только в условиях контролируемого (планируемого) эксперимента. Кроме того, необходимо, чтобы в конкретной выборке каждый из введенных в модель факторов обладал достаточной вариабельностью в смысле влияния на отклик, что можно выяснить, исключая каждый фактор из модели и сравнивая полученные до и после исключения значения критерия Фишера. Существенность влияния фактора в конкретных условиях определяется также его значимостью.

Другим осложняющим обстоятельством является мультиколлениарность факторов, т.е. их связность.

Кроме того, в практических исследованиях часто возникает вопрос о том, сколько нужно иметь значений экспериментальных данных для надежного определения коэффициентов уравнения регрессии, однозначного ответа, на который нет. Выбор числа экспериментальных данных определяется требованиями к точности модели, что аккумулируется, в конечном счете, в размере доверительного интервала прогноза.

Еще одним препятствием к применению регрессионного анализа при построении моделей является ограниченность исходной информации, ценность которой может снижаться за счет ее "засоренности", т.е. за счет проявления обстоятельств, которые ранее не были учтены. Резко отклоняющиеся значения экспериментальных данных могут быть результатом действия большого числа сравнительно малых случайных факторов, которые в достаточно редких случаях приводят к большим отклонениям, либо это один или несколько действительно случайных выбросов, которые можно исключить как аномальные. Вопрос об исключении из выборки таких резко отклоняющихся значений должен решаться исследователем в зависимости от конкретных обстоятельств.

С точки зрения оценки адекватности регрессионных моделей недостатком метода регрессионного анализа является то, что критерий среднеквадратической ошибки, рассчитываемый по всем точкам таблицы экспериментальных данных - внутренний, т. е. его определение основано на использовании тех же данных, которые используются и для расчета коэффициентов уравнения регрессии. А любой внутренний критерий сравнения моделей приводит к ложному правилу: чем сложнее модель, тем она точнее.

Однако, несмотря на указанные сложности и недостатки, регрессионные модели находят достаточно широкое применение при описании реальных объектов и явлений, если они строятся с учетом требований, предъявляемых к ним.

Библиографический список.

1. Хорафас Д.Н. Системы и моделирование.-М.: Мир, 1967.-419 с.

2. Смит Дж.М. Математическое и цифровое моделирование для инжене­ров и исследователей.- М.: Машиностроение, 1980.- 271 с.

3. Горстко А.Б. Познакомьтесь с математическим моделированием.- М.: Знание, 1991.- 157 с.

4. Бусленко В.Н. Автоматизация имитационного моделирования слож­ных систем.- М.: Наука, 1977.- 239 с.

5. Ивченко Г.И. Теория массового обслуживания / Г.И. Ивченко, В.А. Каштанов, И.Н. Коваленко.- М.: Высшая школа, 1982.- 256 с.

6. Зуховицкий С.И. Математические методы сетевого планирования / С.И. Зуховицкий, И.А. Радчик. - М.: Наука, 1965.- 296 с.

7. Геловани В.А. Проблемы компьютерного моделирова­ния / В.А. Геловани, В.В. Юрченко. - М.: МНИИПУ, 1990. - 237 с.

8. Молчанов А.А. Моделирование и проектирование сложных систем.- Киев: Выща школа, 1988.- 360 с.

9. Львовский Е.Н. Статистические методы построения эмпирических формул.- М.: Высшая школа, 1988.- 239 с.

10. Основы математического моделирования локомотивов на ЭВМ: учеб. пособие / Е.С. Павлович [и др.]. – Самара : СамИИТ, 1996. – 54с.

11. Математическое моделирование локомотивов и машин в расчетах на ЭВМ: методические указания к выполнению контрольной работы для студентов специальностей 150700- Локомотивы, 180700-Электрический транспорт, 170900- Подъемно-транспортные, дорожные и строительные машины и оборудование / Ю.Е. Просвиров [и др.]. – Самара : СамИИТ, 1998. – 22 с.

12. Ермаков Ю.Д. Методические указания к выполнению РГР по дисциплине «Математическое моделирование локомотивов в расчетах на ЭВМ» Ю.Д. Ермаков, Ю.Е. Просвиров, В.С. Целиковская. – Самара, 1993. – 19с.

Приложение 1