Два основных интуитивных принципа наивной теории множеств.

1. Интуитивный принцип объемности.

Утверждение, что любое множество однозначно определяется своими элементами можно сформулировать по-другому: два множества равны тогда и только тогда, когда они состоят из одних и тех же элементов. Обозначения: A = B – равенство множеств;

A B – неравенство множеств.

Следуя принципу объемности, доказательство равенства двух множеств проводится в два этапа:

Любой элемент должен принадлежать В.

Любой элемент должен принадлежать А.

из 1) и 2) следует, что A = B.

Пример 1.

Доказать, что множество всех положительных целых четных чисел равно множеству всех положительных чисел, представимых как сумма двух целых положительных нечетных чисел.

Доказательство.

Пусть

Тогда

Пусть

Тогда

Пример 2.

т. к. пустое множество не равно множеству, состоящему из одного элемента.

Множество задается перечислением элементов в фигурных скобках, только если элементов в нем мало. В противном случае прибегают к другому способу задания множества: при помощи характеристического предиката (предикат в переводе с латинского – высказывание, свойство). Под высказыванием будем понимать любое повествовательное предложение, которое можно охарактеризовать как истинное или ложное. Под характеристическим предикатом от x будем понимать последовательность, состоящую из слов, математических символов и символа x, которая превращается в высказывание, если всюду вместо x подставить конкретный объект, выбранный из определенного множества. Всякий одноместный предикат можно считать функцией одного переменного x. Значения функции – это высказывания, а область определения – некоторое множество объектов. Предикат может быть двух- трех - ,…, n – местным.

Пример 3.

Двухместный предикат x + y = 10.

Обозначения предиката: P(x), Q(x, y), R(x₁, x₂, …, x_n).

2. Интуитивный принцип абстракции.

Любой предикат P(x) задает некоторое множество A посредством условия, согласно которому в А входят те и только те элементы а, которые обращают P(а) в истинное высказывание. Так как всякое множество однозначно определяется своими элементами, то любой характеристический предикат определяет в точности одно множество А: Обозначение  множество таких элементов а, что P(а)  истинное высуказывание.

Пример 1.

 множество точек окружности радиуса 1 с центром в начале координат.

Пример 2.

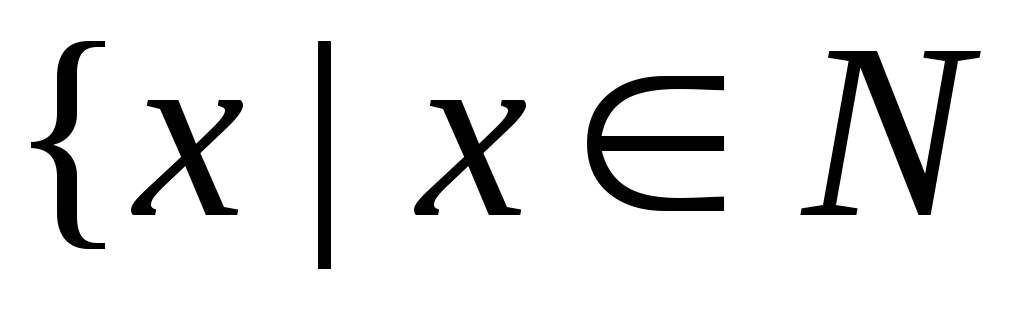и x не имеет делителей  множество простых чисел.

Если заранее известно, из какого множества отбираются элементы, то пишут:

Пример 3.

или

Если y не входит в описание предиката P(x), то следующие множества равны:

В противном случае равенство не обязательно.

Принципы объемности и абстракции основаны на двух исходных понятиях: множества и принадлежности; если понятием принадлежности пользоваться слишком свободно, то возникают парадоксы, например, парадокс Рассела.

Парадокс Рассела.

Все множества, которые мы рассматривали, не содержат себя в качестве своих элементов: Если множество содержит себя в качестве своего элемента, то запишем, что

Пусть Y - множество всех таких множеств, которые не содержат себя в качестве своих элементов:

Вопрос:

Очевидные рассуждения приводят к противоречию: и наоборот. Это противоречие возникает из-за слишком свободного обращения с понятием характеристического предиката. В дальнейшем потребуем, чтобы характеристический предикат был таким и только таким, чтобы существовал алгоритм, позволяющий за конечное число шагов определить истинность или ложность предиката для каждого объекта x. Для бесконечного множества не существует алгоритма, который за конечное число шагов определил бы истинность или ложность утверждения , значит, не является характеристическим предикатом в нашем понимании, а Y – не множество. В дискретной математике рассматривают только конечные множества, элементы которого можно точно описать за конечное число шагов, значит, противоречия подобного рода возникать не могут.