Частичный порядок в решетке.

В любой решетке можно ввести нестрогий частичный порядок, если положить, что

1. Рефлексивность:

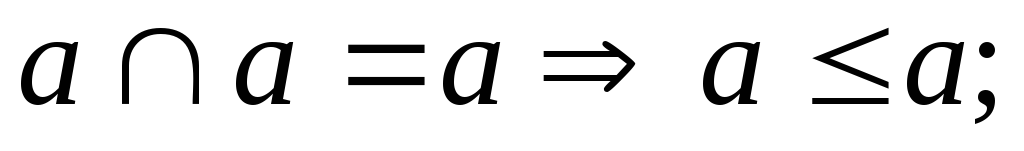
2. Антисимметричность:

Пусть и и ;

3. Транзитивность:

Пусть и и

.

Часто решетку определяют, начиная с нестрогого частичного порядка.

Пусть М – частично упорядоченное множество с нестрогим порядком . Если во множестве М для любых двух его элементов a, b существуют их точные верхняя и нижняя грани (sup(a,b)) и (inf(a,b)), то элементы множества М образуют решетку, если положить: ab = inf (a,b) и ab = sup (a,b).

Докажем выполнение аксиом 1 – 4:

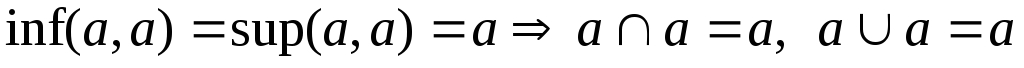1. – идемпотентность;

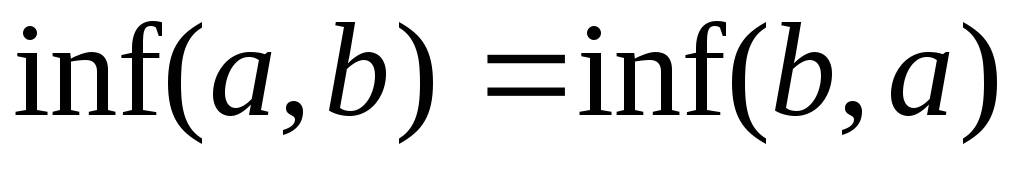2. и и 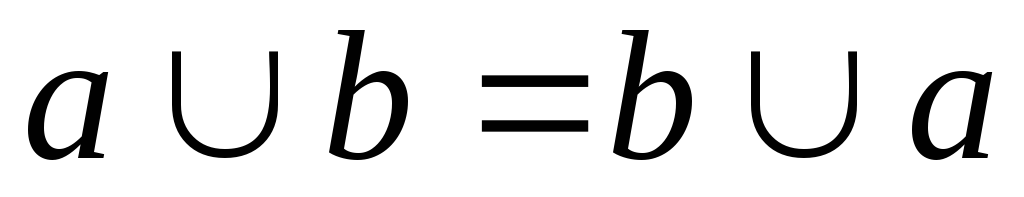– коммутативность ;

3. 

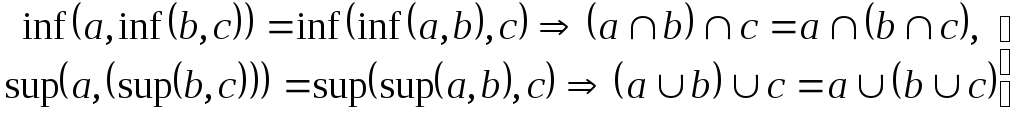
–ассоциативность;

4. – законы поглощения.

Лекция 11. Матроиды.

Пусть Е – конечное множество |Е| = n,   семейство подмножеств множества Е, и каждый элемент x из множества E принадлежит хотя бы одному множеству из . Пара (Е, ) образует матроид, если выполняются три аксиомы матроида:

М.1: 

М.2: Если В  и А  В, то А  

М.3: Если |В| = |А| + 1 и А, В , то (e В\А): А{e}

Множества, входящие в семейство  называются независимыми, остальные (2ⁿ \) множеств, называются зависимыми. Аксиому М.3 можно заменить на эквивалентную ей аксиому М.3: Если А, В и |В| > |А|, то (e В\А): А{e}.

Примеры.

1. Е – конечное множество векторов конечномерного линейного пространства, семейство  образуют всевозможные наборы линейно независимых векторов, взятых из Е.

Доказательство.

М.1: ; (пустое множество векторов линейно независимо)

М.2: Любое подмножество линейно независимых векторов линейно независимо;

М.3: Пусть А = , . Из теории конечномерных векторных пространств известно, что существует вектор , который не выражается линейно через векторы множества А    - множество линейно независимых векторов. Значит, (Е, ) – матроид.

2. Свободные матроиды. Пара (Е, 2^Е) образует матроид, который называется свободным.

3. Матроиды разбиений. Пусть {E_i} – разбиение множества Е, E_i= Е, E_i  Е_j =, если i ≠ j, Е ≠ . Определим семейство  так:

 = {A|}.

Другими словами, в любое независимое множество входит не более одного элемента из каждого множества разбиения.

Пример.

E = {1, 2, 3, 4}, E₁ = {1}, E₂ = {2, 4}, E₃ = {3}.

A₁ =, A₂ = {1}, A₃ = {2}, A₄ = {3}, A₅ = {4}, A₆ = {1, 2}, A₇ = {1, 3},

A₈ = {1, 4}, A₉ = {2, 3}, A₁₀ = {4, 3}, A₁₁ = {1, 2, 3}, A₁₂ = {1, 3, 4}.

Докажем, что выполняются аксиомы матроида.

М.1: , так как .

М.2: Если В   и А  В,  А  , так как условие очевидным образом выполняется.

М.3: Пусть А, В, |A| = k, |B| = k +1  (E_i):|B E_i | = 1, |AE_i | = 0 .

Максимально независимые подмножества.

Пусть X  E и Y  X. Множество Y называется максимально независимым подмножеством множества X, если Y независимо (Y) и (eX\Y): Y{e}. Это подмножество называется еще базой или базисом множества X. Базы Е называются базами матроида. Множество всех баз данного множества X обозначается .

Рассмотрим матроид разбиения из предыдущего примера.

E = {1, 2, 3, 4}, X = {1, 2, 4}, {1, 2} и {1, 4}.

Е, {1, 2, 3}, {1, 3, 4}.

М.4: Все базы данного множества X равномощны.

Доказательство.

Пусть Y и Z, но |Y||Z|, например |Y|>|Z|. Так как Y и Z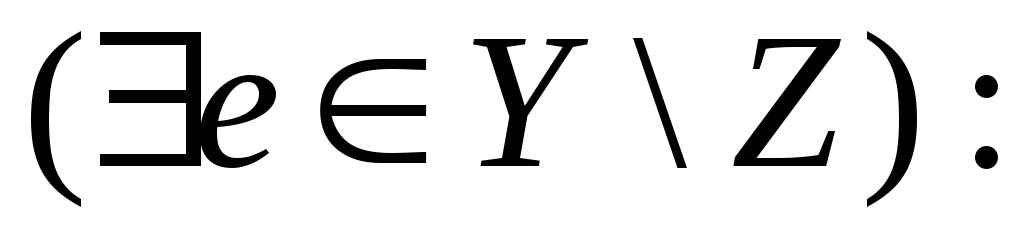  Z{e}. Но Z{e}X, и Z – не максимально независимое подмножество множества X. Мы получили противоречие, базы должны быть равномощны. Таким образом, М.4 следует из М.2 и М.3.

Докажем, что М.3 следует из М.2 и М.4, т.е. условия М.3 и М.4 взаимозаменяемы.

Доказательство.

Предположим, что М.2 и М.4 выполняются. Докажем, что выполняется М.3 (от противного). Пусть A, B, |B| = k + 1, |A| = k, но М.3 не выполняется. Тогда (eВ\А): А{e}. Положим С = В  А

1. А  С, А – база С,

2. B  C, B, следовательно, В или база множества С, или B можно

увеличить до базы, добавив в него элементы из А. Нарушено условие М.4, базы должны иметь равные мощности.