Функции.

Функцией называют бинарное отношение , обладающее следующим свойством: если и . Это означает, что если определён первый элемент упорядоченной пары, то второй элемент определяется единственным образом.

Это свойство функции называют однозначностью. Обозначения функции: , , .

Если y = f(x), то элемент x из множества Х называют аргументом функции или прообразом элемента y , а элемент y – значением функции или образом элемента x.

Условие однозначности означает, что у всякого прообраза есть единственный образ.

Областью определения функции f называют множество ее прообразов: . Если область определения совпадает с Х, то функция называется тотальной.

В дальнейшем будем считать, что функции тотальны.

Областью значений функции f называют множество ее образов. Если область значений совпадает с множеством Y, функция называется сюръекцией или сюръективной (от фр. Sur  на). О сюрьективной функции говорят, что она отображает множество Х на множество Y.

По аналогии с n – арными бинарными отношениями можно говорить о функции n аргументов (f: X₁×X₂× … ×X_n → Y).

Пример.

1. {(1, 1),(1, 2),(2, 4),(3, 6)}  RR не функция, а бинарное отношение;

2. {(1, 1),(2, 4),(3, 6)}- функция с областью определения {1, 2, 3} и областью значений {1, 4, 6};

3. {(x, y)| y = x², x, y  R} – функция RR⁺.

Инъекции и биекции.

Пусть . Эта функция называется инъективной или инъекцией (от лат. injectio  впрыскивание), если . Другими словами, у каждого образа есть единственный прообраз.

Функцию называют биективной или биекцией, если она одновременно инъективна и сюръективна. Биекцию по-другому называют взаимно-однозначным соответствием между областью определения и областью значений: каждому x из области определения функция f ставит в соответствие единственный y из области значений и, наоборот: для каждого yY существует единственный xX: y = f(x).

Изобразим разные типы функций с помощью картинок.

Рис.2. Бинарное отношение,

но не функция

Рис.3. Инъекция, но не

сюръекция

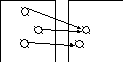
Рис.4. Сюръекция, но не

инъекция

Рис.5. Тотальная биекция

Т.к. функция – это бинарное отношение, то можно построить обратное бинарное отношение , которое необязательно является функцией. Условие однозначности может быть нарушено. Сформулируем условие, которое обеспечивает бинарному отношению свойство функции (или условие однозначности).

Теорема.

Пусть  тотальная биекция, тогда отношение также является тотальной биекцией.

Доказательство.

1. Докажем, что  функция.

, т.к. функция f – инъекция (у каждого образа y есть единственный прообраз x).

2. – тотальна, = Y, т.к. f – сюръекция.

3. – сюръекция, т.к. f – тотальна.

Итак, если f – тотальная биекция, то все элементы множества X – прообразы (тотальность), а все элементы множества Y – образы (сюръекция). Тогда, по определению , все элементы множества Y становятся прообразами (тотальность), а элементы множества X становятся образами (сюръекция).

4. Докажем, что 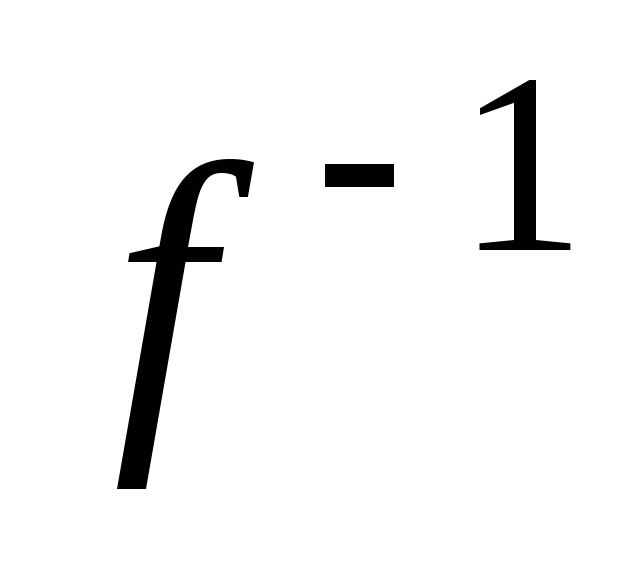– инъекция. Допустим, что это не так: : . Но тогда противоречие, т.к. f – функция.

Пусть A  X, тогда по определению . Множество называется образом множества А. Пусть B  Y, тогда по определению . Множество называется прообразом множества В.