
- •Тема 1. Элементы квантовой механики
- •Корпускулярно-волновые свойства света.
- •1.2 Соотношения неопределенностей Гейзенберга.
- •1.3.Волновое уравнение частицы.
- •1.4. Движение частиц через потенциальный барьер. Туннельный эффект.
- •1.5 Линейный гармонический осциллятор.
- •1.6 Электрон в атоме водорода
- •Тема 2. Кристаллические решётки
- •2.1 Структура и виды кристаллических решёток, их характеристики.
- •2.2 Дефекты реальных кристаллических материалов их влияние на свойства твердых тел.
- •Тема 3. Элементы зонной теории твердых тел
- •3.1.Обобществление электронов в кристалле. Зонный характер энергетического спектра электронов в кристалле.
- •Ядра соседних атомов, притягивая электрон, ослабляют его связь
- •В результате взаимодействия одни уровни смещаются вверх,
- •3.2. Зоны Бриллюэна. Число уровней в разрешённых зонах. Заполнение зон электронами и электрические свойства твердых тел
- •3.3. Зонные диаграммы металлов, полупроводников и диэлектриков.
- •3.3. Статистика электронов и дырок в полупроводниках
- •Тема 4. Статистика носителей зарядов в полупроводниках и металлах
- •4.1.Основные понятия статистической физики.
- •4.2 Микрочастицы и макроскопические системы . Термодинамическое и статистическое описание идеального электронного газа.
- •4.3. Концентрация электронов и дырок в собственном полупроводнике
- •4.4. Концентрация электронов и дырок в примесном полупроводнике
- •Определение положения уровня Ферми
- •4.5.Неравновесные носители
- •Тема 5. Электропроводность твердых тел
- •5.1 Тепловое движение и его средняя скорость.
- •5.3 Дрейфовый ток
- •5.4.Диффузионный ток
- •Эффект Холла
- •5.6.Эффект Ганна.
- •Тема 6.Поверхностные явления в полупроводниках
- •Тема 7. Контактные явления и электрические переходы
- •7.1 Работа выхода электронов из металла и полупроводника.
- •7.2 Контакт металл-металл. Контактная разность потенциалов.
- •7.3.Термоэлектрические явления
- •7.4.Контакт металл-полупроводник: выпрямляющий (барьер Шотки) и невыпрямляющий (омический) контакты
- •7.6. Прямое включение p-n-перехода.
- •7.7. Обратное включение p-n-перехода.
- •7.8 Инжекция неосновных носителей
- •7.9. Вольт-амперная характеристика идеального р - n перехода
- •7.10 Отличие вольт-амперной характеристики р-n перехода от теоретической
- •7.11.Туннельный эффект в электронно-дырочном переходе.
- •Тема 8. Физические основы оптоэлектроники и квантовой электроники 4 часа
- •8.1.Основные понятия фотометрии. Основные энергетические и фотометрические величины.
- •8.2.Фотопроводимость полупроводников.
- •8.3.Фотоэлектрические эффекты в p-n-переходе. Влияние светового потока на вах p-n-перехода.
- •8.4. Основные виды генерации оптического излучения в полупроводниках:
- •8.6. Внешняя квантовая эффективность
- •8.7.Энергетические спектры атомов, молекул и твердых тел.
- •8.8.Спектральные свойства активной среды. Ширина спектральной линии, причины ее уширения.
- •8.10.Методы создания инверсии населенностей.
- •Тема 9. Физические основы вакуумной и плазменной электроники
- •9.2 Типы эмиссии:
- •9.3 Термоэлектронные катоды
- •9.7.Токопрохождение в вакууме. Конвекционный, наведенный и полный ток.
- •9.8 Электрический разряд в газах. Возбуждение и ионизация атомов газа.
- •1.2. Задачи
- •Пример решения
- •2. Статистика носителей зарядов в полупроводниках и металлах 4 часа
- •2.1. Краткие теоретические сведения
- •2.2 Задачи для решения
- •3.1. Краткие теоретические сведения
- •3.2. Задачи
- •3.3. Примеры решения задач
- •4. Поглощение и излучение света 4 часа
- •4.2 Задачи
- •4.3 Примеры решения задач
Тема 2. Кристаллические решётки
2.1 Структура и виды кристаллических решёток, их характеристики.
Кристаллическое тело характеризуется правильным расположением атомов в пространстве. У аморфных веществ расположение атомов случайно. Кристаллические вещества образуют кристаллическую решётку.
Кристаллическая решётка характеризуется элементарной ячейкой.
Элементарная ячейка – кристаллическая решётка наименьшего объёма, воспроизведение которой в пространстве множество раз создаёт пространственную кристаллическую решётку. Атомы в пространстве располагаются упорядоченно, образуя кристаллическую решётку.
Основу симметрии бесконечной кристаллической решётки составляет её пространственная периодичность — способность совмещаться с собой при параллельных переносах (трансляциях) на определённые расстояния в определённых направлениях. Эквивалентные узлы кристаллической решётки, которые могут быть совмещены друг с другом путём трансляции, образуют Браве решётку. Их существует 14 типов.
По симметрии Браве решётки делятся на 7 кристаллических сингоний. Кроме того, кристаллическая решётка может обладать осями и плоскостями симметрии, зеркально-поворотными и винтовыми осями и плоскостями зеркального скольжения. Совокупность осей и плоскостей симметрии, определяющая симметрию физических свойств кристаллов, называется кристаллическим классом; их 32.

Совокупность всех элементов симметрии кристаллической решётки называется её пространственной группой. Всего возможно 230 различных пространственных групп
Для описания элементарной ячейки кристаллической решетки используют 6 величин:
-
Три отрезка,
равные расстояниям a,b,c(периоды
решетки) до
ближайших частиц по осям координат, и
три угла ![]() между этими отрезками. Соотношения
между этими величинами определяются
симметрией, согласно которой все
кристаллы подразделяют на 7 систем.
между этими отрезками. Соотношения
между этими величинами определяются
симметрией, согласно которой все
кристаллы подразделяют на 7 систем.
- Координационное число – число ближайших равноудаленных частиц (для ОЦК – К8, для простой кубической решетки – К6, для ГЦК – К12).
- Коэффициент компактности – отношение объема всех частиц, приходящихся на 1 элементарную ячейку, ко всему объему элементарной ячейки (для простой кубической решетки 0,52, для ОЦК – 0,68, для ГЦК – 0,74).
- Кристаллографические индексы (Индексы Миллера): Они выбираются следующим образом. Зададим начало координат на узле решетки и из семейства интересующих нас параллельных плоскостей выберем ближайшую к нему. Определим (в единицах постоянных решетки) координаты точек пересечения осей [100], [010] и [001] этой плоскостью. Пусть это будут (не обязательно целочисленные) ni. Затем возьмем обратные им величины: 1/n1, 1/n2 и 1/n3 и домножим их на произвольное число g, так, чтобы получить целые числа. Естественно, минимальные из возможных. Набор целочисленных значений (g/n1, g/n2, g/n3) и есть индексы Миллера.
-
Индексы
направления
– выражаются целыми числами ![]() в единицах отрезков
в единицах отрезков ![]() ,
заключаются в квадратные скобки
,
заключаются в квадратные скобки ![]() .
.
-
Индексы
плоскости –
определяют положение плоскости в
пространстве. Выражаются целыми числами
![]() в единицах отрезков
в единицах отрезков ![]() .
За индексы берутся обратные отрезки:
.
За индексы берутся обратные отрезки:
![]() .
.
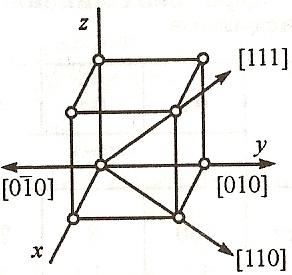
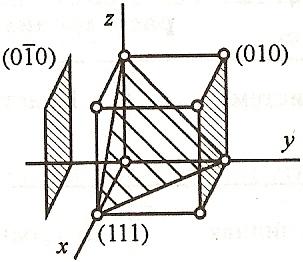
Рис.2.1
