Критическая скорость

(5)

или (6)

где .

Опытным путем установлено, что c=22,4, по данным других исследователей с=25 или 23,4.

Для определения Re_кр чаще всего используется формула Е.М. Соловьева

, (7)

справедливая в диапазоне .

При анализе течения в кольцевом канале диаметр d заменяется на эквивалентный .

2). Собственно турбулентное течение.

Характеризуется флуктуацией скоростей частиц по всем направлениям. Появляются вихри в результате отрыва пограничного ламинарного слоя. Возникают дополнительные, более высокие напряжения сдвига.

Вывести зависимость между расходом Q и давлением P не удается даже для ньютоновских жидкостей, поэтому используются полуэмпирические теории турбулентности.

Л. Прандтль ввел понятие так называемой динамической скорости:

, (8)

где x – постоянный коэффициент, не зависящий от свойств жидкости;

y – расстояние от стенки трубы.

Проинтегрировав (8) и используя данные опытов И. Никурадзе, Прандтль получил расчетные формулы для профиля скоростей и коэффициента гидравлического сопротивления:

, (9)

(10)

k – эквивалентная шероховатость труб, м (0,02-0,04мм для новых труб).

Формула (9) предназначена для области гладкого трения (гладкие трубы), (10) – для области квадратичного трения (вполне шероховатые трубы). Гидравлически гладкими трубы считают в том случае, когда ламинарный подслой, прилегающий к стенке канала, имеет толщину больше, чем шероховатость стенки.

Для шероховатых труб чаще используется формула Колбрука-Уайта

(11)

А.Д. Альтшуль получил широко распространенную ныне формулу:

(12)

При движении ньютоновских жидкостей в гладких трубах применяют также эмпирическую зависимость Блазиуса (1913г.):

(13)

Она дает удовлетворительные результаты при Re=2500÷70000.

При течении вязкопластичных жидкостей наибольшее распространение получила формула Шищенко:

, (14)

где – обобщенный параметр Рейнольдса . Она справедлива при =2500÷50000.

При >50000 значение λ обычно принимают постоянным, равным 0,02.

С учетом сказанного выше, градиент давления

, Па/м (15)

а полное давление

, Па. (16)

Потери давления на местных сопротивлениях

Местные сопротивления появляются из-за изменения проходного сечения (сужение и расширение канала) и направления потока, т.е. они приурочены к соединениям БТ, промывочным каналам коронок и долот, гидромониторным насадкам долот, переходникам и т.п. В таких элементах происходит завихрение потока, отрыв пограничного слоя, сжатие и расширение потока.

Расчет потерь давления выполняют по формуле Вейсбаха:

, (1)

где ξ – коэффициент местного сопротивления; v – средняя скорость (как правило, за зоной возмущения); ρ – плотность среды.

Коэффициент ξ зависит от конфигурации зоны возмущения, режима течения, реологических свойств среды и шероховатости.

Наиболее известен анализ коэффициента ξ Борда и Карно для резкого изменения площади проходного сечения.

Для резкого сужения канала ими предложена формула

, (2)

где ξ₁ – коэффициент на входе; ξ₂ – коэффициент на выходе; D – диаметр канала; d – минимальный диаметр в сужении.

В действительности утолщения бурильных труб сглажены и фактические потери давления в этих зонах ниже вычисленных по (2).

Если сравнить сужение проходного сечения в замковом соединении с конфузором, за которым следует диффузор, то можно использовать следующие полуэмпирические соотношения

Для конфузор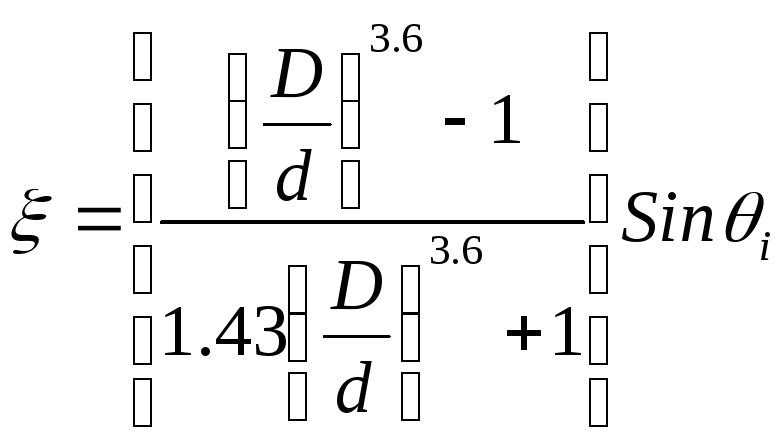а

(а)

для диффузора

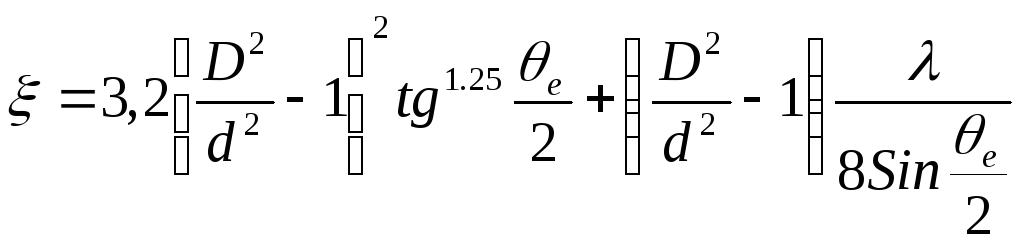(б)

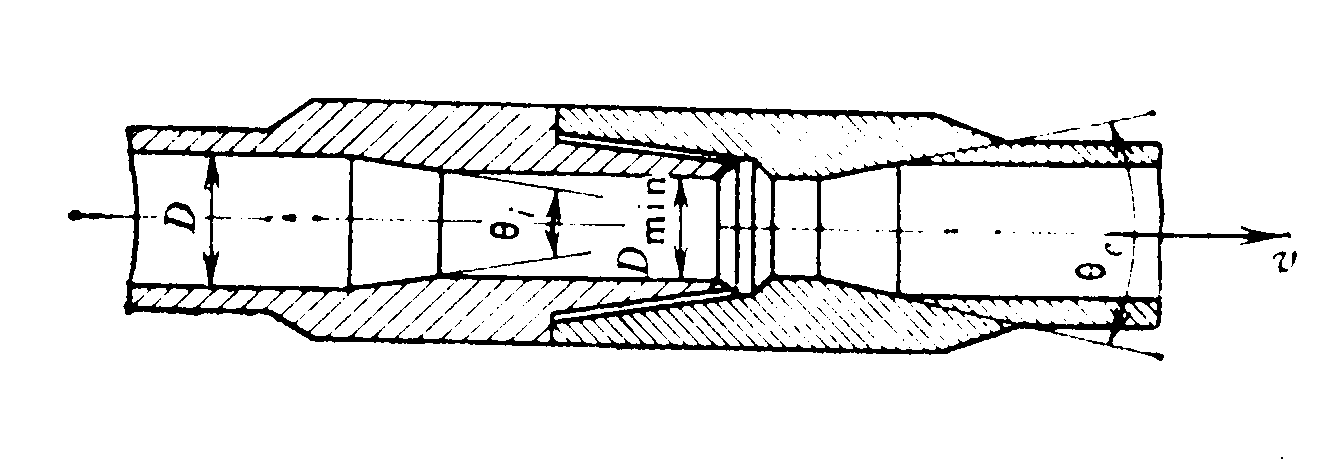
Геометрия замкового соединения бурильных труб.

с обозначениями, показанными на рисунке. Уравнение (а) пригодно при =045°. Поскольку угол входа потока в замковое соединение относительно мал (=15—20°), поток сохраняет устойчивость (нет отрыва пограничного слоя и отсутствуют застойные зоны) и коэффициент пренебрежимо мал по сравнению с .

Следует особо отметить некоторые выводы, к которым пришли в результате проведенных исследований: заметное влияние угла выхода и незначительное угла входа, а также влияние критерия Re при значениях вплоть до 10000. Таким образом, при изменениях числа Re от 2000 до 20000 коэффициент уменьшается в несколько раз и только затем стабилизируется.

При отсутствии экспериментальных данных для обычных замковых соединений можно использовать формулу Борда— Карно с коэффициентом . Потери давления в замковых соединениях бурильной колонны составляют 5—10 % потерь давления в бурильных трубах.

Для геологоразведочных труб муфто-замкового соединения в (2) используют коэффициент 2, для труб ниппельного соединения – 1,5.

Потери давления на местных сопротивлениях (у замковых соединений) в кольцевом пространстве скважин, как правило, незначительны. Однако в узком кольцевом пространстве их следует учитывать по формуле (1), в которой ξ определяют по формуле

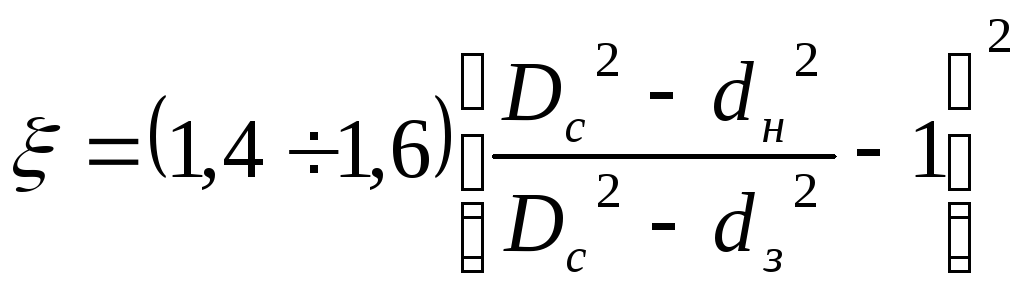, (3)

где D_c – диаметр скважины; d_н – наружный диаметр труб; d_з – наружный диаметр соединений.

При бурении электробурами в соединениях находятся кабельные разъемы, увеличивающие гидравлические сопротивления, при этом потери давления в замках составляют 60÷80% потерь давления в гладкой части труб.