2.2. Реологические модели

Реологические уравнения являются математическими моделями, отражающими идеальное поведение реальных тел.

2.2.1. Фундаментальные модели

Все природные тела в той или иной степени обладают тремя основными свойствами: упругостью, вязкостью и пластичностью. Этот факт и привел к созданию трех базовых моделей. С достаточно высокой точностью они описывают поведение многих категорий природных материалов.

Модель идеально упругой среды характеризует поведение твердого тела, в котором деформация исчезает одновременно с напряжением. Механическая работа, совершаемая под действием внешних нагрузок, ведет к накоплению потенциальной энергии, которая при устранении этих нагрузок возвращает телу исходную форму и размеры. Теоретически деформация является мгновенной, т. е. независимой от времени. При незначительных деформациях зависимость между напряжением и деформацией является линейной функцией (рис. 2.1 а), которая для простого (одноосного) сдвига описывается законом Гука

 =G (2.2)

где  - угловая деформация; G - поперечный модуль упругости (реологическая постоянная тела).

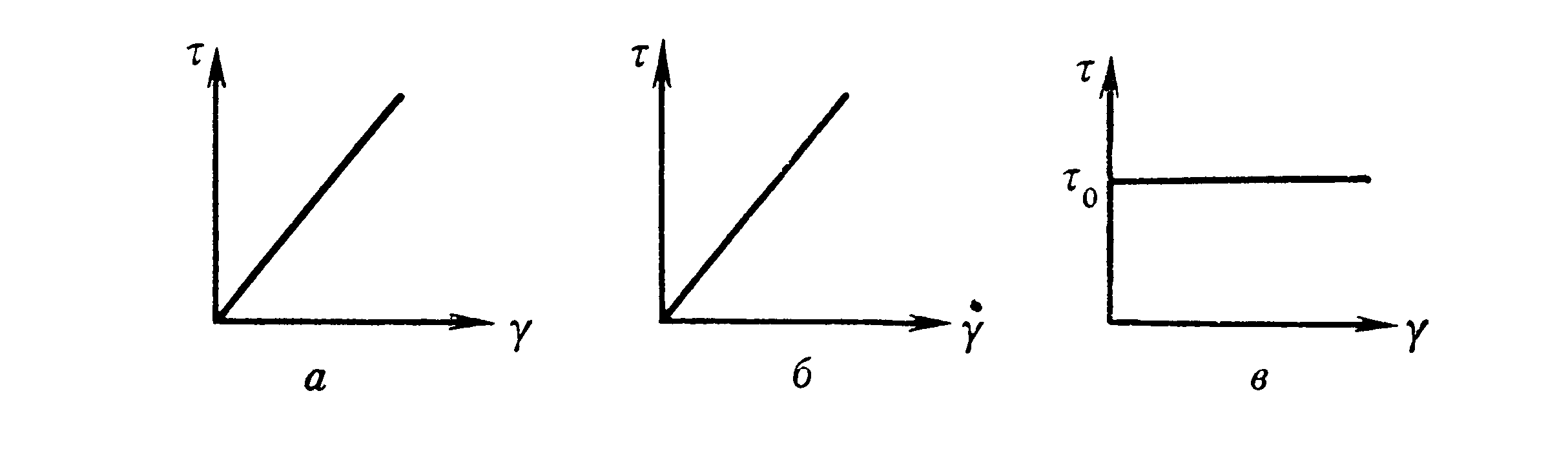Рисунок 2.1. Кривые течения для фундаментальных моделей

а – идеально упругая среда, б – идеально вязкая среда, в – жестко-пластичная среда

Модель идеально вязкой среды отражает линейное отношение между возникающими в жидкости напряжениями и скоростью деформации (рис. 2.1б). При простом сдвиге это соотношение называется законом Ньютона:

 = (2.3)

где — реологическая постоянная модели, или вязкость; — скорость деформации, вызванная касательным напряжением .

Уравнение (2.3), в основном, определяет текучесть газов, воды и некоторых однофазных сред с низкой молекулярной массой.

Можно отметить сходство уравнений (2.2) и (2.3), хотя последнее зависит еще и от времени; при анализе течения представляют интерес не деформации (которые, кстати, очень велики), а скорости деформации, т. е. скорости движения, течения. Скорость деформации пропорциональна действующим напряжениям, а деформация увеличивается пропорционально времени и сохраняется после устранения напряжений.

Модель жесткопластической среды (Сен-Венана) характеризует тела, не поддающиеся деформированию до определенного значения напряжения или предела пластичности, при превышении которого наблюдаются остаточные деформации, а напряжение остается постоянным (рис. 2.1 в). При снятии нагрузки деформация сохраняет максимальное значение, достигнутое под действием напряжения. Такое поведение описывается следующими соотношениями:

, если ,

, если , (2.4)

где - реологическая константа, называемая пределом пластичности (текучести).

Время в этом случае не играет никакой роли, что отличает пластическую текучесть от вязкой. При вязком течении энергия, затраченная на определенную деформацию, зависит от скорости деформации, при пластическом течении такой зависимости нет.

Таким образом, фундаментальные модели характеризуются одной реологической постоянной.

2.2.2. Сложные модели

Многие материалы имеют реологическое состояние, которое невозможно описать ни одной из основных моделей. В связи с этим были созданы модели с двумя и более реологическими постоянными.

Вязкопластическая модель Бингама описывает вещества, которые при напряжениях ниже критического значения , названного предельным напряжением сдвига или динамическим напряжением сдвига, не деформируются, а при больших напряжениях текут подобно вязким жидкостям (рис. 2.2). Реологические уравнения при этом имеют вид:

, если (твердое состояние);

, если (вязкопластичное состояние) (2.5)

У этой модели два реологических параметра: и . Параметр назван пластической (структурной) вязкостью.

Таким образом, Бингам признал за некоторыми жидкостями пластические свойства.

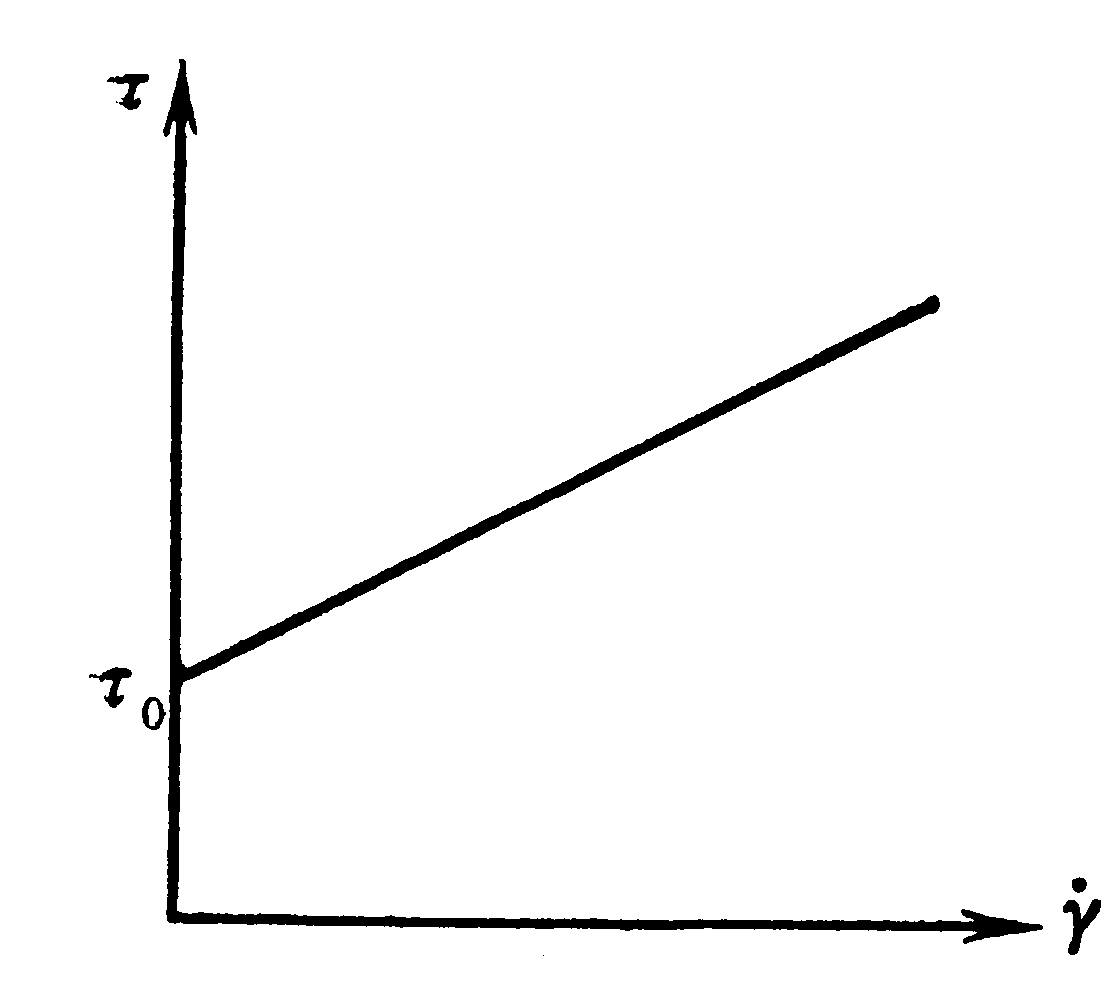
Рис. 2.2. Кривая течения вязкопластичного тела Бингама.

Жидкость, соответствующую модели Бингама, можно рассматривать как ньютоновскую среду с переменной вязкостью. Если сравнить закон Ньютона (2.3) со вторым уравнением (2.5), получим

(2.6)

(2.6)

где — кажущаяся (или эффективная) вязкость, зависящая от скорости деформации . Эффективную вязкость обозначают и как .

Все жидкости, не подчиняющиеся закону Ньютона, т. е. не обладающие постоянной вязкостью, называются неньютоновскими.

К жидкостям, поведение которых можно описать при помощи модели Бингама-Шведова, относятся суспензии (в эту категорию входит большинство буровых и тампонажных растворов), масляные краски, некоторые смазки, пищевые продукты и т. д.

Путем сочетания трех основных моделей были предложены многочисленные комплексные модели, которые используются в различных разделах реологии [1,2,3].

Из моделей, полученных экспериментальным или полуэмпирическим путем, буровиков интересуют только те, которые применимы для жидкостей, обладающих неньютоновским поведением, т. е. подчиняющихся уравнению

(2.7)

с переменной вязкостью (рис. 2.3 и 2.4).

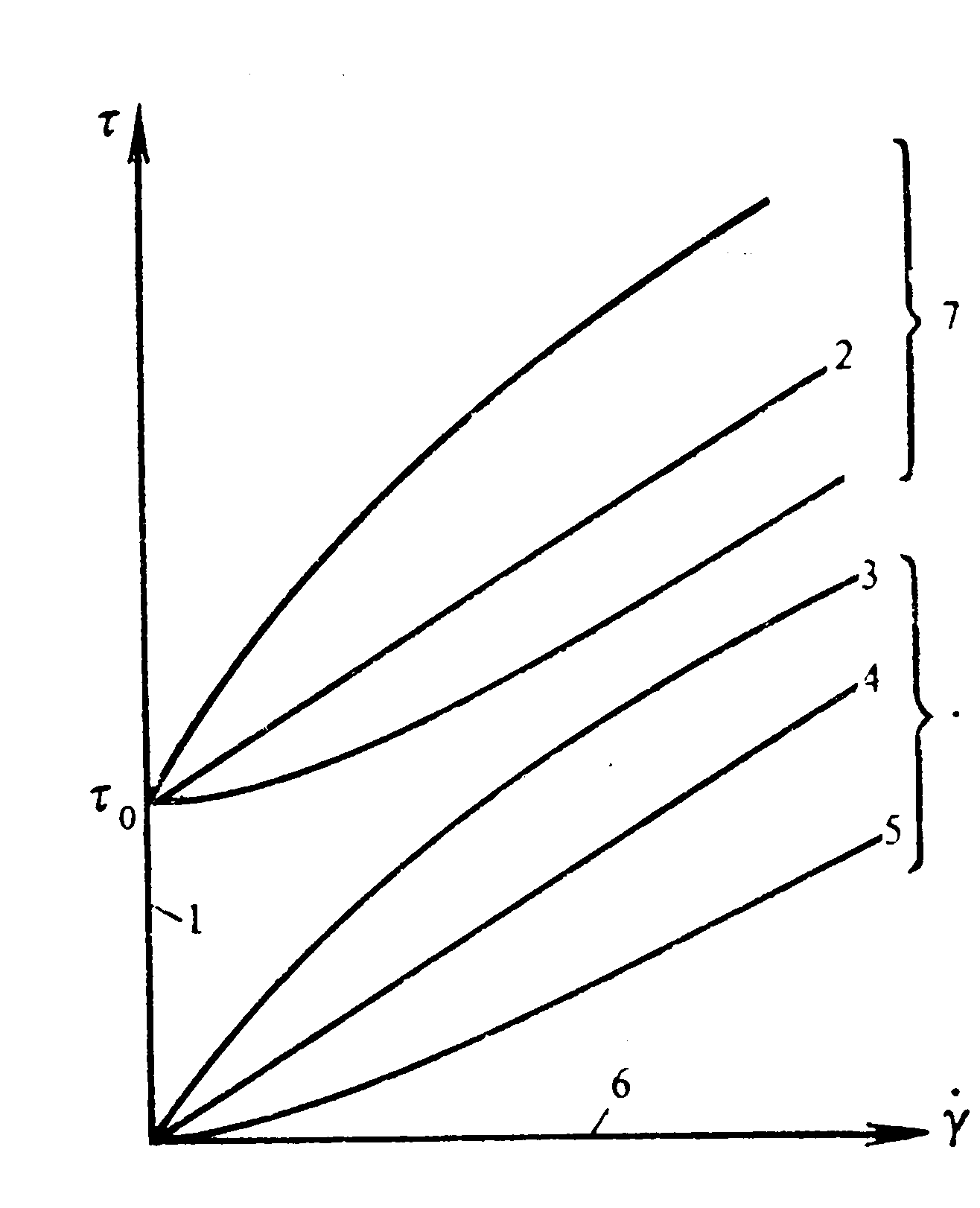
Рис. 2.3. Кривые течения «чисто» вязких жидкостей:

1 – упругое твердое тело, 2 – бингамовская жидкость, 3 – псевдопластичная жидкость, 4 – ньютоновская жидкость, 5 – дилатантная жидкость, 6 – идеальная жидкость, 7 – вязкопластичные жидкости, 8 – жидкости без предельного напряжения сдвига.

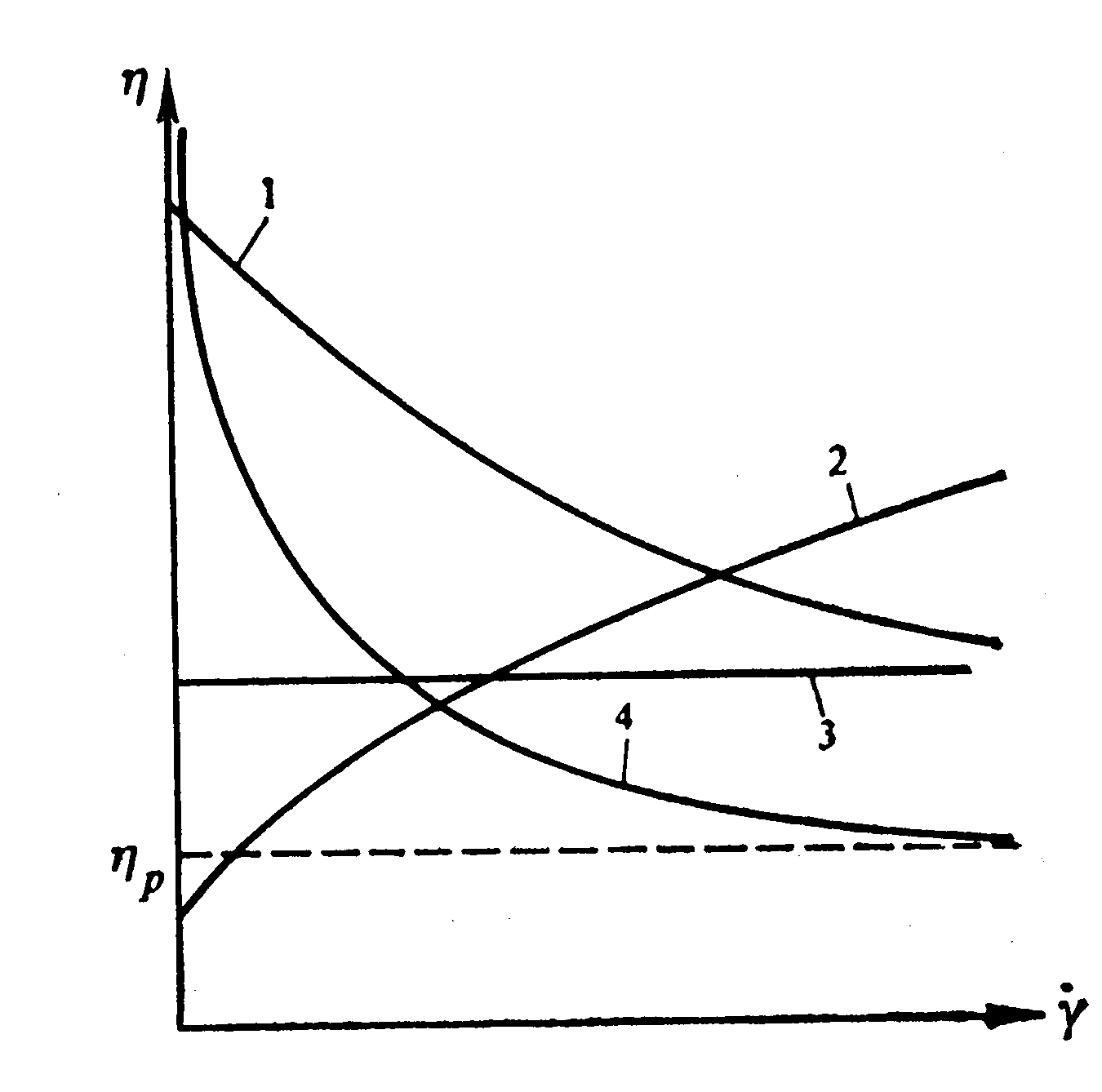
Рис. 2.4. Вязкость «чисто» вязких жидкостей:

1 – псевдопластичная жидкость, 2 – дилатантная жидкость, 3 – ньютоновская жидкость, 4 – бингамовская жидкость

Как правило, вязкость уменьшается с увеличением напряжения или скорости деформации, вещества разжижаются, становятся более подвижными. Это объясняется выравниванием, ориентированием взвешенных несимметричных твердых частиц суспензий или развертыванием цепей полимеров таким образом, что течению оказывается минимальное сопротивление. Среды, для которых характерны кривые течения, проходящие через начало координат, называются псевдопластичными.

Реже встречаются жидкости, вязкость которых увеличивается с повышением скорости деформации. Это объясняется разрушением агрегатов твердых частиц, ориентация которых в состоянии покоя направлена на уменьшение пустот между ними, а также увеличением «пористости» суспензии; часть жидкости перемещается в образовавшиеся пустоты и между частицами начинает проявляться так называемое сухое трение, смазка оказывается недостаточной и трение увеличивается. Такой процесс наблюдается в системах с высокой концентрацией твердой фазы и в грубых дисперсиях: водных суспензиях с высокой концентрацией песка, барита, малоколлоидной глины, слюды, металлических окислов и др. Эти материалы и вещества называются дилатантными.

Некоторые смолы и полимеры (например, полихлорвинил) проявляют псевдопластичное поведение при низких скоростях деформации и дилатантное при более высоких скоростях сдвига.

Для описания течения жидкостей, не обладающих пластическими свойствами (предельное напряжение ), чаще всего пользуются моделью Оствальда—де Ваале с двумя реологическими параметрами

(2.8)

где K и п — экспериментальные константы: K — индекс консистенции; п — показатель поведения.

Из сопоставления уравнения (2.8) с законом Ньютона получим значение эффективной вязкости в виде

(2.9)

Можно видеть, что при п=1 уравнение (2.8) приводится к обычной форме закона Ньютона, при этом , отклонение показателя п от единицы указывает на степень неньютоновского поведения жидкости. При п<1 жидкость является псевдопластичной, а при п>1— дилатантной.

Уравнение (2.8) описывает экспериментальные кривые течения большинства неньютоновских непластичных жидкостей в диапазоне умеренных скоростей деформации. При очень низких или очень высоких значениях скоростей деформации кривые течения могут быть линеаризованы и представлены обычным уравнением закона Ньютона.

При помощи модели Оствальда — де Ваале можно описать поведение некоторых эмульсий, пены, паст, мыльных составов, полимерных растворов, буровых и тампонажных цементных растворов с различными добавками.

Из более сложных моделей (с тремя параметрами) следует отметить модель Гершеля-Балкли (трехпараметрическая, получена сочетанием вязкопластичной модели с моделью Оствальда - де Ваале)

. (2.10)

Она была использована для описания поведения некоторых буровых растворов с низким содержанием твердой фазы, обработанных полимерными реагентами.

В бурении встречаются среды (например, вязкоупругие разделители бурового и тампонажного растворов, горные породы), поведение которых может быть описано реологическим уравнением Кельвина - Фойхта:

. (2.11)

Полное напряжение складывается из двух составляющих: создает линейные упругие деформации, а — вязкие деформации, задерживающие развитие первых. Модель характеризуется двумя реологическими константами: G и . Она представляет комбинацию моделей Гука и Ньютона.

Если проинтегрировать уравнение (2.11), то при , t=0 и (рис. 2.5) получим

(2.12)

где — время ретардации (задержки). Упругость проявляется в этом случае не сразу, а с некоторой задержкой во времени. Деформация растет непрерывно при постоянном напряжении; это явление известно под названием ползучести.

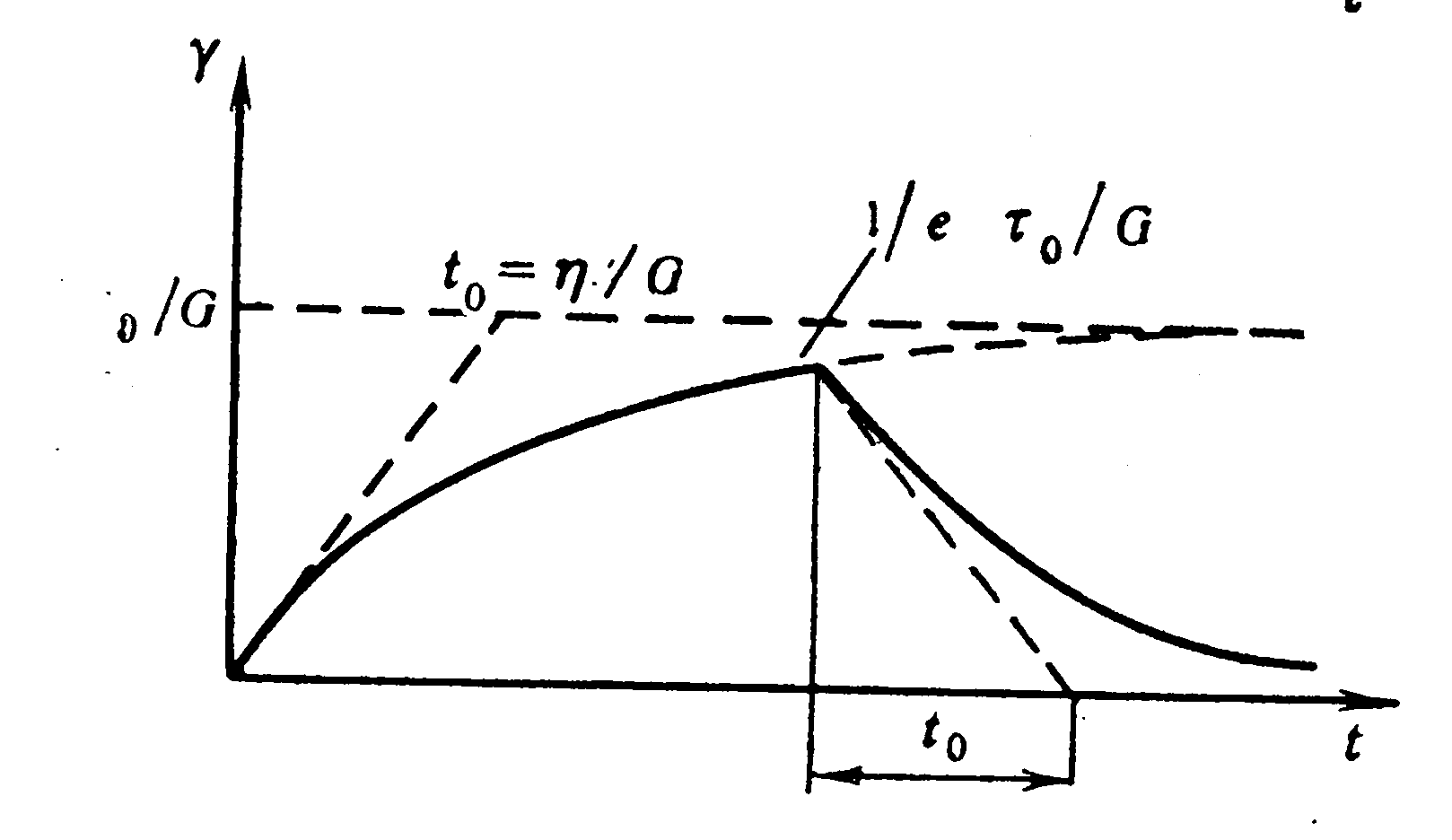
Рис. 2.5. Упругость твердого тела Кельвина-Фойхта

При снятии напряжения деформация исчезает не мгновенно, а медленно уменьшается в соответствии с формулой

, (2.13)

где - деформация в момент снятия напряжения.

Следовательно, модель Кельвина—Фойхта представляет твердое тело с запаздывающей упругостью. Она может использоваться для описания поведения отдельных полимеров, горных пород, а также для описания текучести бетонов, некоторых растворов, металлов и т. д.

Вязкоупругая жидкость Максвелла представляет собой комбинацию моделей Гука и Ньютона и характеризуется следующим реологическим уравнением:

. (2.14)

Скорость деформации имеет две составляющие: упругую и вязкую .

При помощи уравнения Максвелла можно описать как процесс текучести, так и релаксацию напряжений. Если напряжение поддерживать постоянным и равным то, то из уравнения (2.14) следует постоянство скорости деформации, что означает вязкое течение, аналогичное течению ньютоновской жидкости:

(2.15)

где — начальная деформация.

Если предположить, что при воздействии напряжения то в теле возникает мгновенная упругая деформация , то уравнение (2.15) примет вид

. (2.16)

Кривая текучести в данном случае есть прямая с углом наклона (рис. 2.6). Если на материал в момент времени t=0 воздействует напряжение , то при постоянстве деформации из уравнения (2.14) следует, что

, (2.11)

где — время релаксации.

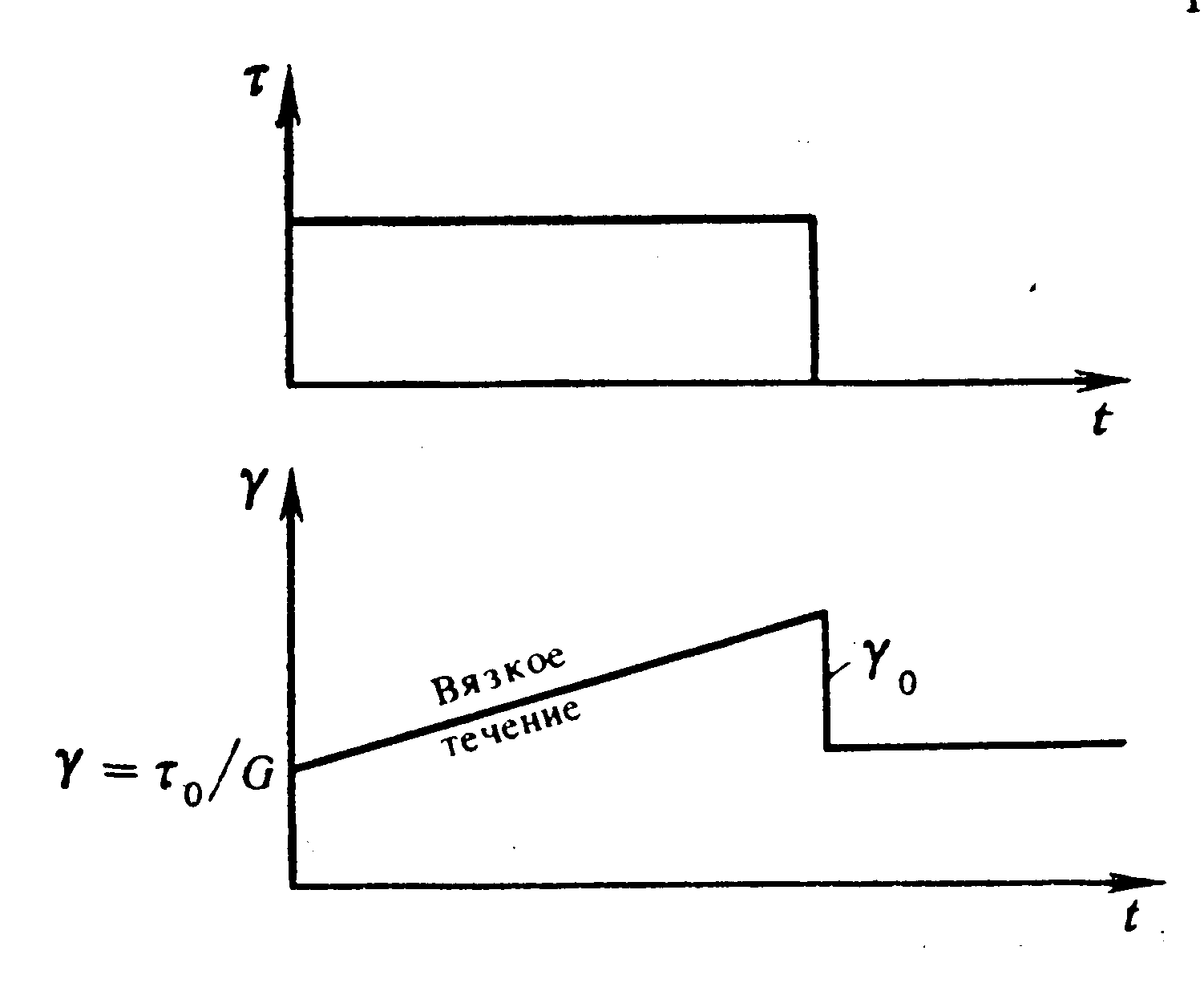
Рис. 2.6. Текучесть жидкости Максвелла